【电机绘图】:插补算法（一）—直线插补—逐点比较法

今日介绍学习一种使用电机作画、绘图、加工零件时需要使用的算法 ： 插补算法

本文提供直线插补的概念基础，基本思路分析，C语言实现等，代码会直接贴出！

插补算法是指在数值计算或数据处理中，根据已有的数据点或采样点，推断出未知数据点或采样点的值的方法。

插补算法可以通过已知数据点之间的关系来填补数据间的空缺或缺失值，从而恢复完整的数据。

在图像处理、信号处理、曲线拟合等领域中，插补算法被广泛应用。

常见的插补算法有线性插值、最邻近插值、多项式插值和样条插值等。插补算法可以帮助我们填补数据缺失的部分，从而更好地分析和处理数据。

目录

概念引入--优化的拟合直线:

直线插补—逐点比较法公式：

 进给情况一：在第一象限的进给与插补

 进给情况二：在第二象限的进给与插补

逐点比较法的总结：

直线插补—逐点比较法 的C实现：

效果展示：

 代码给出：

结束语：

---

概念引入--优化的拟合直线:

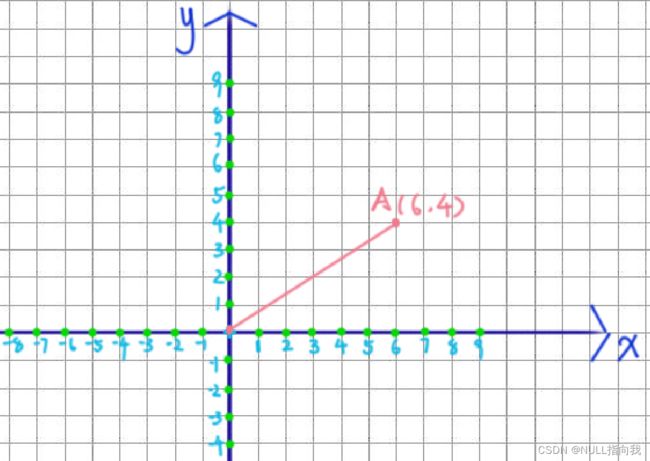
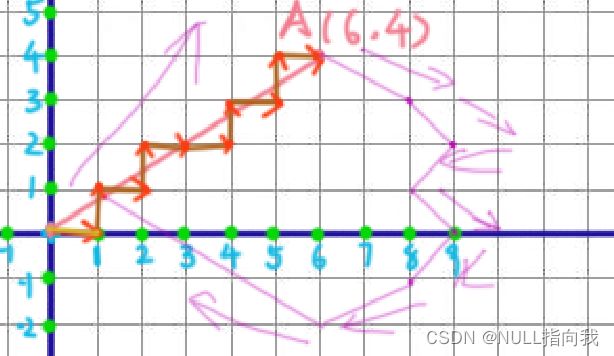
如图：这有一条直线需要我们进行弥合绘制，它的起点是原点（0,0），终点目标是A（6,4）

 我们很容易想到：

因为它的俩个端点固定，因此在数学计算关系式上，我们对其进行补足时，只需计算其斜率：

k=（4-0）/  (6-0)  =  2/3  ;然后将这个运算关系带入电机控制移动，X走一格时，Y同时走2/3，

直到到达点A即可~~

但现实却不会这样：

如果我们的机械电机设计精度远大于这个需求长度分度要求，我们可以尝试使用这个求斜率的办法去弥合绘制该曲线，但实际与理论相悖，

在微观层面，计算机与加工电机或者加工刀具是无法做到如此精准的绘制与定位的，在加工的时候，不同的产品有各式各样的形状。计算机对其直线上每个点的定位，在微观上总是不准确的：

简单的形状，可以轻松的实现。如位置点，只需要确定xy位置，电机运动到xy点上，就能够加工成功。

但是对于比较复杂的形状，此时如果我们去考虑它所有的运行轨迹，所有的运动位置点，这样会非常复杂，计算机的工作量也会大大的增加。

因此在实际应用中，对于复杂的形状，我们无法精确地确定每个点的位置，而是通过数据密化，尽可能的去拟合它真实的形状，通过这种方式，不仅能在达到精度要求的前提下，还能够大大减小计算机的工作量，这就是“插补”。

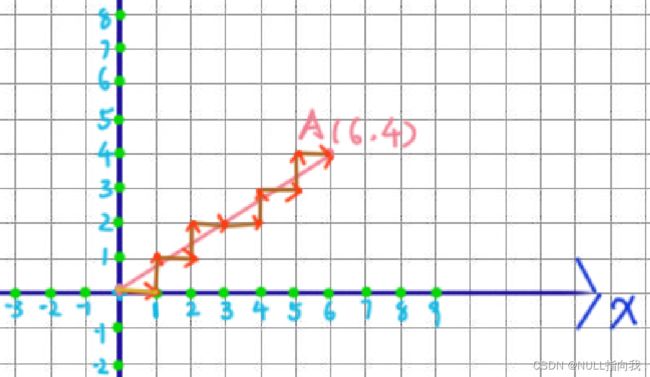
 下图即是对插补的理解画法：

其中我们需要抽离三个概念：

1.理论直线轨迹（肉眼轨迹）                   ——粉色直线

2.实际运行轨迹（机械轨迹）                   ——棕色折线

3.实际给进点情况（X、Y机械运行步骤）——红色箭头

                                                                （向上向下是给Y，向做向右是进给X）

 我们从此图可以看出，这种对于不是45度角度斜率的直线的弥合，我们并不是每次只需，X进1，Y进1就可了，而是有某些部分是需要多进给的，就比如此图，它就在（3,2）后又在此多进给了X一次，以达到对于2/3这个斜率的更佳弥合~~

直线插补—逐点比较法公式：

以下公式是指源于旧的基础上进行运算得出新的F值：

F  =  F  -   |Ye|           (F>=0)

F  =  F  +  |Xe|           (F < 0 )

 

 进给情况一：在第一象限的进给与插补

我们直接看到之前的题目：它在第一象限，看看如何理解使用这个公式：

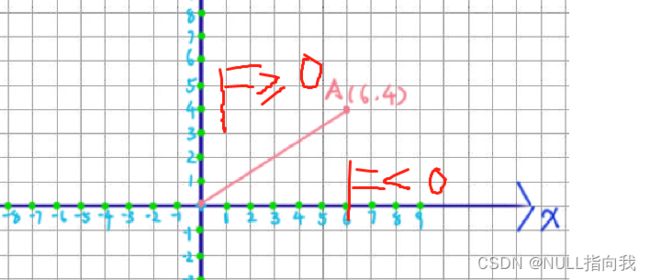
F>=0      表示只能在X坐标上进给

F<0        表示只能在Y坐标上进给

首先我们需要初始化一些数据，它们的值与运算关系如下：

F=0；

E=|Ax|+|Ay|     (终点判断,大小与目标点的横纵坐标有关)

在插补过程中每走一步要完成以下4个工作节拍。

①偏差判别   ——

判别当前动点偏离理论曲线的位置（即F旧）。这是有基础公式的

②进给控制   ——

确定进给坐标及进给方向。这是需要根据终点象限不同，而有所变化的，有的象限进给X表示在X轴加一，有的象限则是在X轴减一

③新偏差计算 ——

迸给后动点到达新位置，计算出新偏差值（即F新），作为下一步判别的依据。

④终点判别    ——

查询一次，终点是否到达。

步数 （一共是E）	偏差判断 （F旧）	坐标进给 （X或Y： 注意象限）	坐标 （X,Y）	偏差计算 (F新)	终点判断 E
0			（0,0）	F（0,0）=0	10
1	F（0,0）=0	+X	（1,0）	F（1,0）=0-4 =-4	9
2	F(1,0)=-4	+Y	（1,1）	F(1,1)=-4+6=2	8
3	F(1,1)>0	+X	(2,1)	F(2,1)=2-4=-2	7
4	F(2,1)<0	+Y	(2,2)	F(2,2)=-2+6=4	6
5	F(2,2)>0	+X	(3,2)	F(3,2)=4-4=0	5
6	F(3,2)=0	+X	(4,2)	F(4,2)=0-4=-4	4
7	F(4,2)<0	+Y	(4,3)	F(4,3)=-4+6=2	3
8	F(4,3)>0	+X	(5,3)	F(5,3)=2-4=-2	2
9	F(5,3)<0	+Y	(5,4)	F(5,4)=-2+6=4	1
10	F(5,4)>0	+X	(6,4)	F(6,4)=4-4=0	0

这样，在编写绘图程序的时候，只需这样一次一次安排好下次插补直线的终点坐标，便可以自己设计，绘制各种各样的复杂形状：

 

 

 进给情况二：在第二象限的进给与插补

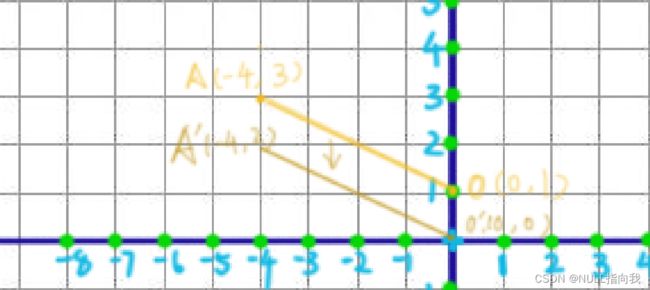
 这次，我们的情况有所改变，不仅目标变为了第二象限的点（-4,3），起点也变为（0.1），而插补计算肯定是要从原点（0,0）开始的，此时，该如何安排电机的运作呢？

 其实，我们这里就要分为俩个步骤：

1.移动到新起点

2.计算新终点的坐标

 此处我们肯定希望起点还是原点（0,0）的，因此在电机运动的程序设计上，可以使其先移动到（0,1）后开始插补绘制，为保持斜率不变，新的A点坐标也要随之改变为（-4,2）。

第二象限，乃至其余象限，直线插补的公式不会改变，但是进给X、Y时的加减是会改变的，

比如此处的插补，终点坐标经过我们修改后是（-4,2），由此终点坐标判断可得出：

在X轴的进给变为负的，在Y轴方向的进给仍是正的 原理就是判断终点坐标的正负即可

 

下面我们继续绘制图表来帮助理解过程：

步数 （一共是E）	偏差判断 （F旧）	坐标进给 （X或Y： 注意象限）	坐标 （X,Y）	偏差计算 (F新)	终点判断 E
0			（0,0）	F（0,0）=0	6
1	F（0,0）=0	-X	（-1,0）	F（-1,0）=0-2=-2	5
2	F（-1,0）<0	+Y	（-1,1）	F（-1,1）=-2+4=2	4
3	F（-1,1）>0	-X	（-2,1）	F（-2,1）=2-2=0	3
4	F（-2,1）=0	-X	（-3,1）	F（-3,1）=0-2=-2	2
5	F（-3,1）<0	+Y	（-3,2）	F（-3,2）=-2+4=2	1
6	F（-3,2）>0	-X	（-4,2）	F（-4,2）=2-2=0	0

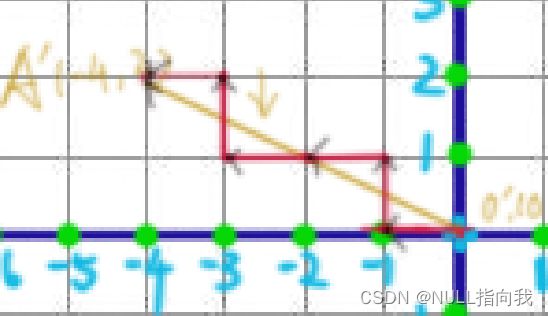
最终弥合效果如下图：

 

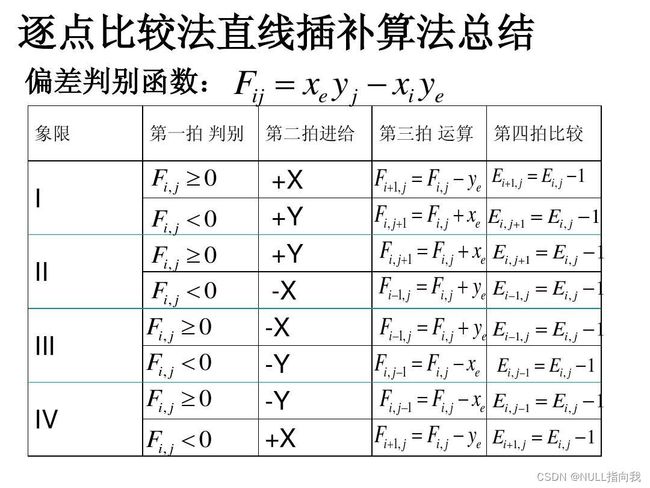
逐点比较法的总结：

这是我从网上盗的图，可以看看归纳，帮助理解 ：

 

直线插补—逐点比较法 的C实现：

这里展示我编写的C代码，它使用逐点比较法实现了各个象限的直线插补，只需输入目标点的坐标，就会自动识别在哪个象限，并且会打印输出每一步的过程坐标，

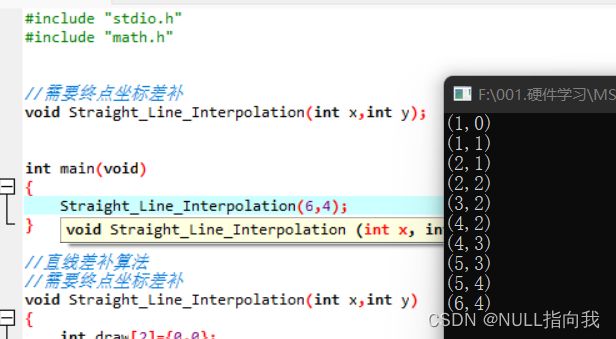
效果展示：

 代码给出：

#include "stdio.h"
#include "math.h"


//需要终点坐标差补 
void Straight_Line_Interpolation(int x,int y);


int main(void)
{
	Straight_Line_Interpolation(6,4);
}

//直线差补算法 
//需要终点坐标差补 
void Straight_Line_Interpolation(int x,int y)
{
    //当前点坐标
	int draw[2]={0,0};

	//E:终点判断 
	//F:偏差计算 
	//i:当前插补步数（最终要等于E） 

	int E,F,i;
	E=abs(x)+abs(y);
	F=0;
	
//循环次数就是E决定的
	for(i=0;i=0) 
	  {
        //再根据判断终点X,Y在哪个象限，决定进给情况
	  	if(x>0)        {draw[0]+=1;}
		else if(x<0)   {draw[0]-=1;}		 

        //计算本次产生的新的偏差F 
	     F=F-abs(y);
	     printf("(%d,%d)\r\n", draw[0], draw[1]);
	  }

       //先判断偏差F，决定进给X还是Y
	  else if(F<0) 
	  {
        //再根据判断终点X,Y在哪个象限，决定进给情况
	  	if(y>0)       {draw[1]+=1;} 
		else if(y<0)  { draw[1]-=1; }

        //计算本次产生的新的偏差F 
	   	F=F+abs(x);
	    printf("(%d,%d)\r\n", draw[0], draw[1]);	
   	
	   }
	}
}

结束语：

最后希望这篇文章对大家有用，喜欢可以三连支持一下~~~~~~