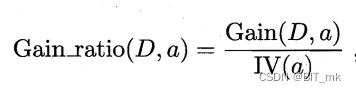吃瓜教程-Task03

基本流程

决策树基于树的结构来进行决策

图中叶子节点对应决策结果，而其他的每个节点对应于每个属性的测试。从根结点到每个叶结点的路径对应了一个判定测试序列。

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树。

采用分而治之的的策略。

算法伪代码

递归过程中有三种情况会递归返回。

1. 当前结点包含的样本全属于同一类别，无需划分。
   这意味着你已经找到一个纯净的叶子节点，所有的样本点都是同一类别。因为这个节点已经“纯净”，所以没有必要继续在这个节点上进行属性划分了，算法在这个节点上的递归就会停止。
2. 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分
3. 当前结点包含的样本集合为空，不能划分。

在第 2 种情形下我们把当前结点标记为叶结点，井将其类别设定为 该结点所含样本最多的类别 ;在第 3 种情形下，同样把当前结点标记为叶结点 将其类别设定为其父结点所含样本最多的类别 .注意这两种情形的处理实质不同:情形2 是在利用 当前结点的后验分布 ，而情形 3 则是把 父结点的样本分布作为当前结点的先验分布。

先验分布与后验分布：

1. 先验分布：在获取观察数据之前，我们对一个随机变量（比如参数）的概率分布的主观判断。这是贝叶斯分析中的一个基本概念，它代表了在没有观察到任何数据之前，我们对于一个或多个未知参数的不确定性。

2. 后验分布：在获取观察数据后，我们根据贝叶斯定理更新对随机变量的概率分布的认识。它是在已知某个结果发生后，参数的概率分布，基于先验分布和已知数据计算得出。

注意：当所有样本在某个节点上的所有属性值取值相同时，也不能说明这个节点是纯净的。纯净特指的是所属类别相同。

比如，假设你在建立一个预测是否喜欢阅读的决策树，有两个人，他们的属性（年龄，性别，职业等）都完全相同，但一个人喜欢阅读，另一个人不喜欢。这时候，虽然他们的属性完全相同，但是他们所属的类别（喜欢阅读，不喜欢阅读）不同，所以这个节点是不纯净的。

具体例子，在这个例子中，我们进行一个判断是否喜欢户外运动的任务，我们的数据集是：

1. 天气 = 晴天，温度 = 热，喜欢户外活动 = 否
2. 天气 = 晴天，温度 = 冷，喜欢户外活动 = 是
3. 天气 = 雨天，温度 = 热，喜欢户外活动 = 否
4. 天气 = 雨天，温度 = 冷，喜欢户外活动 = 否

我们通过以上数据来进行模型训练，然后用训练好的模型来进行预测在雨天，温度热的情况下是否喜欢户外运动。

from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import numpy as np

# 创建模拟数据
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([0, 1, 0, 0])

# 0 代表晴天，1 代表雨天
# 0 代表热，1 代表冷
# 1 代表喜欢户外活动，0 代表不喜欢户外活动

# 创建决策树分类器实例
clf = DecisionTreeClassifier(random_state=1234)

# 训练模型
model = clf.fit(X, Y)

# 预测模型
# 假设我们有一个新的观察值，天气是雨天，温度是热的
new_observation = [[1, 0]]

# 使用训练好的模型进行预测
prediction = model.predict(new_observation)

print('预测结果为：', '喜欢户外活动' if prediction == 1 else '不喜欢户外活动')


# 创建特征名称和类别名称列表
feature_names = ['weather', 'temperature']
class_names = ['dislike', 'like']

# 使用plot_tree函数绘制决策树
plt.figure(figsize = (10,8))
tree.plot_tree(model, 
               feature_names = feature_names,  
               class_names=class_names,
               filled = True)
plt.show()

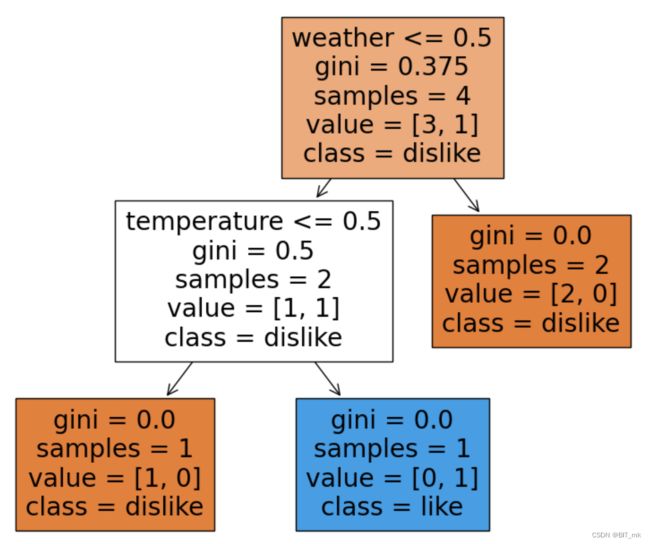
输出结果：

并且我们把决策树进行可视化：

CART决策树使用"基尼指数" (Gini index) 来选择划分属性

 gini系数：

Gini系数（或者说Gini不纯度）被用来衡量一个节点的不纯度。如果一个节点是完全“纯净”的（也就是说，所有的样本都属于同一类别），那么这个节点的Gini系数就是0。相反，如果一个节点的样本均匀地分布在各个类别中，那么这个节点的Gini系数就是最大的（对于二分类问题，最大的Gini系数是0.5）。

gini系数计算公式：

 其中，p是各个类别的概率，k是类别的总数。例如，对于一个二分类问题，如果一个节点的样本中有80%是类别A，20%是类别B，那么这个节点的Gini系数就是：

，gini系数较小，说明这个节点是比较纯净的

samples表示此节点下的样本数

 "values"字段表示的是在该节点处，各个类别的样本数量

---

划分选择

我们划分时希望样本的纯度越来越高。

ID3 决策树 学习算法 就是以信息增益为准则来选择划分属性.

条件熵

计算实例

假设我们有以下数据集，我们要预测一个人是否会打网球(Tennis)，我们有的特征是"Outlook"，"Temperature"，"Humidity"，"Wind"。

Outlook	Temperature	Humidity	Wind	Tennis
Sunny	Hot	High	Weak	No
Sunny	Hot	High	Strong	No
Overcast	Hot	High	Weak	Yes
Rain	Mild	High	Weak	Yes
Rain	Cool	Normal	Weak	Yes
Rain	Cool	Normal	Strong	No
Overcast	Cool	Normal	Strong	Yes
Sunny	Mild	High	Weak	No
Sunny	Cool	Normal	Weak	Yes
Rain	Mild	Normal	Weak	Yes
Sunny	Mild	Normal	Strong	Yes
Overcast	Mild	High	Strong	Yes
Overcast	Hot	Normal	Weak	Yes
Rain	Mild	High	Strong	No

1.首先，计算目标变量 "Tennis" 的熵，称为原始熵。

Yes的次数为9，No的次数为5，总次数为14，所以熵为:

2.其次，计算每个特征对目标变量 "Tennis" 的条件熵。例如，计算 "Outlook" 对 "Tennis" 的条件熵。

Outlook=Sunny的次数为5，其中Yes的次数为2，No的次数为3。

Outlook=Overcast的次数为4，其中Yes的次数为4，No的次数为0。

Outlook=Rain的次数为5，其中Yes的次数为3，No的次数为2。

所以，条件熵为：

3.最后，信息增益是原始熵和条件熵的差：

 python计算代码

import pandas as pd
import numpy as np

# 创建数据集
data = {'Outlook': ['Sunny', 'Sunny', 'Overcast', 'Rain', 'Rain', 'Rain', 'Overcast', 'Sunny', 'Sunny', 'Rain', 'Sunny', 'Overcast', 'Overcast', 'Rain'],
        'Tennis': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No']}
df = pd.DataFrame(data)

# 计算原始熵
value,counts = np.unique(df['Tennis'], return_counts=True)
H_Tennis = sum([(-counts[i]/np.sum(counts))*np.log2(counts[i]/np.sum(counts)) for i in range(len(value))])

# 计算条件熵
value_O,counts_O = np.unique(df['Outlook'], return_counts=True)
H_Tennis_Outlook = 0
for i in range(len(value_O)):
    temp_value, temp_counts = np.unique(df[df['Outlook'] == value_O[i]]['Tennis'], return_counts=True)
    temp_H_Tennis = sum([(-temp_counts[i]/np.sum(temp_counts))*np.log2(temp_counts[i]/np.sum(temp_counts)) for i in range(len(temp_value))])
    H_Tennis_Outlook += (counts_O[i]/np.sum(counts_O))*temp_H_Tennis

# 计算信息增益
Gain = H_Tennis - H_Tennis_Outlook
print("The information gain of Tennis and Outlook is: ", Gain)

 使用entropy函数来计算

import pandas as pd
import numpy as np
from scipy.stats import entropy

# 创建数据集
data = {'Outlook': ['Sunny', 'Sunny', 'Overcast', 'Rain', 'Rain', 'Rain', 'Overcast', 'Sunny', 'Sunny', 'Rain', 'Sunny', 'Overcast', 'Overcast', 'Rain'],
        'Tennis': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No']}
df = pd.DataFrame(data)

# 计算原始熵
p_Tennis = df['Tennis'].value_counts(normalize=True)
H_Tennis = entropy(p_Tennis, base=2)

# 计算条件熵
df_grouped = df.groupby('Outlook')['Tennis']
H_Tennis_Outlook = sum([entropy(group.value_counts(normalize=True), base=2) * (len(group) / len(df)) for name, group in df_grouped])

# 计算信息增益
Gain = H_Tennis - H_Tennis_Outlook
print("The information gain of Tennis and Outlook is: ", Gain)

将各个属性的信息增益值算出来后选择信息增益值最大的作为划分属性。

信息增益主要是度量了一个属性和特征可以给我们的决策带来了多少信息，比如我们在一个果园里闭眼摸水果，假设果园里有苹果和橙子。我们一开始闭眼摸，随便摸一个是无法判断，但如果我们此时引入一个特征颜色，我们观察颜色这个特征后，我们就可以根据颜色来判断出我们是摸的什么水果，这就是信息增益，我们通过颜色这个特征进而减少了信息的不确定性。在决策树算法中，我们希望最大化信息增益，进而减少目标变量的不确定性。

信息增益准则对可取值数目较多的属性有所偏好：

当属性的可取值较多时，按照这个属性进行划分可能会产生较大的信息增益。因为每一个新的属性值都可能创造一个新的分支，也就是一个新的纯净（或者更纯净）的子集。

但是这样有可能会带来一个问题，那就是过拟合。因为可能有一些属性的可取值很多，但这些属性并没有提供太多关于分类结果的信息。比如说，如果我们用一个人的身份证号来预测他的身高，虽然按照身份证号进行划分可以得到完全纯净的子集（每个人的身份证号都不同，所以每个子集中只有一个样本），信息增益也很大，但显然这样的模型没有任何泛化能力，对新的未知样本的预测能力也非常差。

C4.5 决策树算法 不直接使用信息增益，而是使用"增益率" (gain ratio) 来选择最优划分属性

增益率

增益率(Gain Ratio)就是信息增益和固有值的比值。它的主要目的是为了解决信息增益倾向于选择取值多的特征的问题。通过引入固有值，我们在计算信息增益的同时，也考虑了特征的"复杂度"或"混乱度"。 

属性固有值 

固有值(Intrinsic Value，也称为分裂信息量)是一个衡量特征分裂复杂度的度量，它与特征可能的取值数量和这些取值的分布均匀程度有关。对于那些取值多且分布均匀的特征，它们的固有值会很高。因此，我们可以将固有值理解为对一个特征的"复杂度"或"混乱度"的度量。

形象地说，可以将信息增益看作是你的收入，而固有值看作是你的花费。你希望用最小的花费（最小的复杂度，最小的固有值）得到最大的收入（最大的信息增益）。而增益率就是你的"投资回报率"，它度量的是你每花一块钱（每增加一点复杂度）可以得到多少的收入（信息增益）。我们希望这个"投资回报率"尽可能地大，也就是说，我们希望用最小的复杂度得到最大的信息增益。