VanillaNet 原理与代码解读

paper：VanillaNet: the Power of Minimalism in Deep Learning

official implementation： GitHub - huawei-noah/VanillaNet

存在的问题 

虽然复杂网络的性能很好，但它们日益增加的复杂性给部署带来了挑战。例如，ResNets中的shortcut操作在合并不同层的特征时耗费了大量的off-chip memory traffic。再比如AS-MLP中的axial shift操作以及Swin Transformer中的shift window self-attention操作都需要复杂的工程实现，包括重写CUDA代码。

本文的创新点

本文提出了VanillaNet，一种新的神经网络架构，有着简单而优雅的设计，同时在视觉任务中保持了显著的性能。VanillaNet通过舍弃过多的深度、shortcut以及self-attention等复杂的操作，解决了复杂度的问题，非常适合资源有限的环境。

方法介绍

A Vanilla Neural Architecture

大多数SOTA分类网络的架构都包含三个部分：一个stem block将输入图片由3个通道转换为多通道并进行下采样，一个main body提取特征，一个全连接层用来输出分类结果。其中main body通常包含4个stages，每个stage堆叠多个相同的blocks，每个stage后特征图的分辨率降低通道数增加。不同网络的区别主要在于blocks的设计不同。

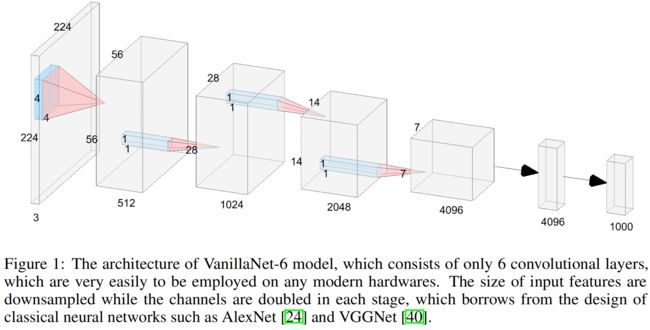
本文提出的VanillaNet也遵循这种流行的设计架构，不同的是，每个stage只包含一层网络层从而构建一个极度简洁的网络。

VanillaNet-6的结构如图(1)所示，具体包括：stem部分是一个stride=4的4x4x3xC的卷积层将3通道的输入图片映射为C通道的feature map。stage1,2,3中，用一个stride=2的maxpooling进行下采样同时通道数翻倍。在stage4中保持通道数不变，因为它后面是一个average pooling层。最后一个全连接层输出分类结果。为了使用最小的计算量所有的卷积层都是1x1大小，每个卷积层后跟一个BN层和一个激活函数。

尽管VanillaNet的结构简单且层数很少，但其较弱的非线性限制了其性能，接下来作者又提出了一系列方法来解决该问题。

Training of Vanilla Networks

Deep Training Strategy

深度训练策略的核心思想是在训练初期训练两个卷积层和一个激活函数而不是只训练一个卷积层。随着训练的进行，激活函数逐渐演变成一个恒等映射。在训练结束时，通过结构重参数化，可以将两个卷积层合并为一个，从而减少推理时间。

对于一个激活函数 \(A(x)\)（例如常见的ReLU和Tanh），我们将它和一个恒等映射结合起来，如下

其中 \(\lambda\) 是一个超参用来平衡修改后的激活函数 \(A'(x)\) 的非线性。假设当前的epoch和训练完整的epoch数分别为 \(e\) 和 \(E\)，我们设置 \(\lambda =\frac{e}{E} \)。这样，在训练刚开始时 \(e=0,A'(x)=A(x)\)，这意味网络具有很强的非线性。当训练收敛完成后，\(A'(x)=x\)，这意味着两个卷积层中间没有激活函数了，我们就可以通过结构重参数化方法将其合并成一个卷积。

Series Informed Activation Function

简单网络和浅层网络的性能较差主要是因为较差的非线性。有两种提高网络非线性的方法：叠加非线性激活层和提高每个激活层的非线性能力。大多数网络选择前者，而本文选择后者，不过也是通过堆叠的方式。（这里文中说前者是serially stacking，而后者是concurrently stacking，个人理解应该都是连续堆叠，只不过前者通常是卷积层和激活函数一起堆叠才导致网络越来越深，而本文是只堆叠激活函数）。

具体是通过加权堆叠的方式，其中 \(n\) 表示堆叠的个数，\(a_{i},b_{i}\) 分别是每个激活函数的scale和bias。通过这种堆叠，激活函数的非线性能力可以大大提高。

式(5)可以看作是数学中的级数series，为了进一步提高series的近似能力，作者使series-based的函数能够通过改变来自neighbors的输入来学习全局信息，类似于BNET。具体对于一个输入特征 \(x\in\mathbb{R}^{H\times W\times C}\)，激活函数可以表示为

其中 \(h\in\left \{ 1,2,...,H \right \} ,w\in\left \{ 1,2,...,W \right \} ,c\in\left \{ 1,2,...,C \right \} \)。

实验结果

VanillaNet的具体结构如表6

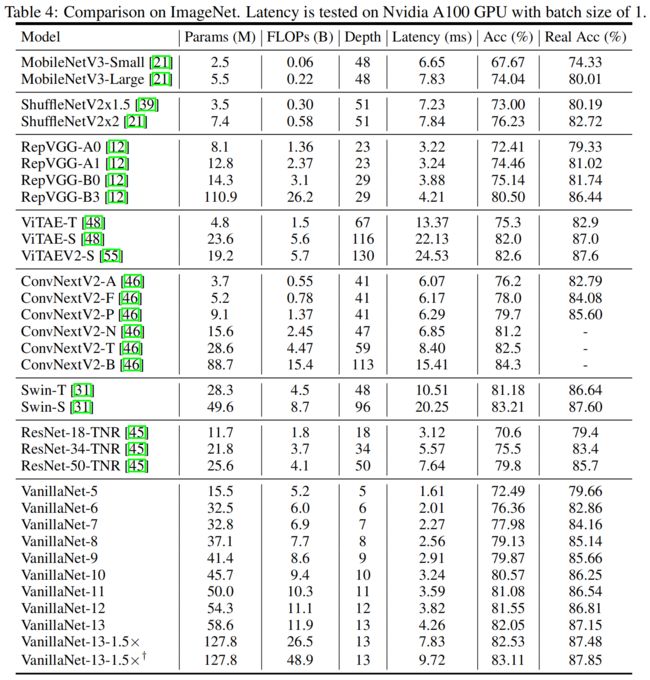
在ImageNet数据集上，和其它一些SOTA模型的对比如表4

 可以看出，VanillaNet仅用10层就取得了80.57的top-1精度，不同的层数下，和相同精度的其它模型相比，具有显著的速度优势。

代码解读

首先是深度训练策略，在models/vanillanet.py中，class VanillaNet()包含了网络的具体实现。其中self.deploy用来表示是否为推理阶段，当self.deploy=False时表示是训练阶段，可以看到stem阶段包含self.stem1和self.stem2，main body阶段每个block都包含self.conv1和self.conv2，最后的全连接层也包含self.cls1和self.cls2。当训练完成后即推理阶段，所有的阶段的1和2之间的激活函数都变成了恒等映射或者说操作1和2之间没有激活函数了，然后通过结构重参数化将operation 1,2合并成1个。

其中self.act_learn即为式(1)中的 \(\lambda\)，在main.py中，act_learn随着训练的进行而变化。

act_learn = epoch / args.decay_epochs * 1.0
model.module.change_act(act_learn)

接着是激活函数的堆叠，这里作者将激活函数的简单加权堆叠即式(5)演变为可以学习临近输入的式(6)后，可以通过深度卷积来实现，其中堆叠个数超参 \(n=3\)，即代码中的self.act_num。

# Series informed activation function. Implemented by conv.
class activation(nn.ReLU):
    def __init__(self, dim, act_num=3, deploy=False):
        super(activation, self).__init__()
        self.act_num = act_num
        self.deploy = deploy
        self.dim = dim
        self.weight = torch.nn.Parameter(torch.randn(dim, 1, act_num*2 + 1, act_num*2 + 1))
        if deploy:
            self.bias = torch.nn.Parameter(torch.zeros(dim))
        else:
            self.bias = None
            self.bn = nn.BatchNorm2d(dim, eps=1e-6)
        weight_init.trunc_normal_(self.weight, std=.02)

    def forward(self, x):
        if self.deploy:
            return torch.nn.functional.conv2d(
                super(activation, self).forward(x), 
                self.weight, self.bias, padding=self.act_num, groups=self.dim)
        else:
            return self.bn(torch.nn.functional.conv2d(
                super(activation, self).forward(x),
                self.weight, padding=self.act_num, groups=self.dim))

    def _fuse_bn_tensor(self, weight, bn):
        kernel = weight
        running_mean = bn.running_mean
        running_var = bn.running_var
        gamma = bn.weight
        beta = bn.bias
        eps = bn.eps
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta + (0 - running_mean) * gamma / std

    def switch_to_deploy(self):
        kernel, bias = self._fuse_bn_tensor(self.weight, self.bn)
        self.weight.data = kernel
        self.bias = torch.nn.Parameter(torch.zeros(self.dim))
        self.bias.data = bias
        self.__delattr__('bn')
        self.deploy = True

疑问

在作者的官方解读卷积的尽头不是Transformer，极简架构潜力无限 - 知乎下也有评论指出，本来式(5)连续堆叠激活函数增加非线性的想法很好，但演变为式(6)后，就又还原成卷积了，激活函数加权相加的权重 \(a_{i,j,c}\) 就是卷积核的权重，官方实现中也是通过depth convolution实现的series informed activation，这样把外面的卷积层移到激活函数里了，能叫层数减少了吗？