SimHash简介以及java实现
转自:
http://www.open-open.com/lib/view/open1375690611500.html
关于 罗刚 老师 搜索解密中的 SimHash算法 、 TITS算法 、标准Trie树、三叉Trie树 java实现 下载地址
http://download.csdn.net/detail/zhuhongming123/8175135
(mkse/simHash目录下)
传统的 hash 算法只负责将原始内容尽量均匀随机地映射为一个签名值,原理上相当于伪随机数产生算法。产生的两个签名,如果相等,说明原始内容在一定概 率 下是相等的;如果不相等,除了说明原始内容不相等外,不再提供任何信息,因为即使原始内容只相差一个字节,所产生的签名也很可能差别极大。从这个意义 上来 说,要设计一个 hash 算法,对相似的内容产生的签名也相近,是更为艰难的任务,因为它的签名值除了提供原始内容是否相等的信息外,还能额外提供不相等的 原始内容的差异程度的信息。
而 Google 的 simhash 算法产生的签名,可以满足上述要求。出人意料,这个算法并不深奥,其思想是非常清澈美妙的。
1、Simhash 算法简介
simhash算法的输入是一个向量,输出是一个 f 位的签名值。为了陈述方便,假设输入的是一个文档的特征集合,每个特征有一定的权重。比如特征可以是文档中的词,其权重可以是这个词出现的次数。 simhash 算法如下:1,将一个 f 维的向量 V 初始化为 0 ; f 位的二进制数 S 初始化为 0 ;
2,对每一个特征:用传统的 hash 算法对该特征产生一个 f 位的签名 b 。对 i=1 到 f :
如果b 的第 i 位为 1 ,则 V 的第 i 个元素加上该特征的权重;
否则,V 的第 i 个元素减去该特征的权重。
3,如果 V 的第 i 个元素大于 0 ,则 S 的第 i 位为 1 ,否则为 0 ;
4,输出 S 作为签名。
2、算法几何意义和原理
这个算法的几何意义非常明了。它首先将每一个特征映射为f维空间的一个向量,这个映射规则具体是怎样并不重要,只要对很多不同的特征来说,它们对所对应的向量是均匀随机分布的,并且对相同的特征来说对应的向量是唯一的就行。比如一个特征的4位hash签名的二进制表示为1010,那么这个特征对应的 4维向量就是(1, -1, 1, -1)T,即hash签名的某一位为1,映射到的向量的对应位就为1,否则为-1。然后,将一个文档中所包含的各个特征对应的向量加权求和,加权的系数等于该特征的权重。得到的和向量即表征了这个文档,我们可以用向量之间的夹角来衡量对应文档之间的相似度。最后,为了得到一个f位的签名,需要进一步将其压缩,如果和向量的某一维大于0,则最终签名的对应位为1,否则为0。这样的压缩相当于只留下了和向量所在的象限这个信息,而64位的签名可以表示多达264个象限,因此只保存所在象限的信息也足够表征一个文档了。
明确了算法了几何意义,使这个算法直观上看来是合理的。但是,为何最终得到的签名相近的程度,可以衡量原始文档的相似程度呢?这需要一个清晰的思路和证明。在simhash的发明人Charikar的论文中[2]并没有给出具体的simhash算法和证明,以下列出我自己得出的证明思路。
Simhash是由随机超平面hash算法演变而来的,随机超平面hash算法非常简单,对于一个n维向量v,要得到一个f位的签名(f<1,随机产生f个n维的向量r1,…rf;
2,对每一个向量ri,如果v与ri的点积大于0,则最终签名的第i位为1,否则为0.
这个算法相当于随机产生了f个n维超平面,每个超平面将向量v所在的空间一分为二,v在这个超平面上方则得到一个1,否则得到一个0,然后将得到的 f个0或1组合起来成为一个f维的签名。如果两个向量u, v的夹角为θ,则一个随机超平面将它们分开的概率为θ/π,因此u, v的签名的对应位不同的概率等于θ/π。所以,我们可以用两个向量的签名的不同的对应位的数量,即汉明距离,来衡量这两个向量的差异程度。
Simhash算法与随机超平面hash是怎么联系起来的呢?在simhash算法中,并没有直接产生用于分割空间的随机向量,而是间接产生的:第 k个特征的hash签名的第i位拿出来,如果为0,则改为-1,如果为1则不变,作为第i个随机向量的第k维。由于hash签名是f位的,因此这样能产生 f个随机向量,对应f个随机超平面。下面举个例子:假设用5个特征w1,…,w5来表示所有文档,现要得到任意文档的一个3维签名。假设这5个特征对应的3维向量分别为:
h(w1) = (1, -1, 1)T
h(w2) = (-1, 1, 1)T
h(w3) = (1, -1, -1)T
h(w4) = (-1, -1, 1)T
h(w5) = (1, 1, -1)T
按simhash算法,要得到一个文档向量d=(w1=1, w2=2, w3=0, w4=3, w5=0) T的签名,
先要计算向量m = 1*h(w1) + 2*h(w2) + 0*h(w3) + 3*h(w4) + 0*h(w5) = (-4, -2, 6) T,然后根据simhash算法的步骤3,得到最终的签名s=001。
上面的计算步骤其实相当于,先得到3个5维的向量,第1个向量由h(w1),…,h(w5)的第1维组成:
r1=(1,-1,1,-1,1) T;第2个5维向量由h(w1),…,h(w5)的第2维组成:
r2=(-1,1,-1,-1,1) T;
同理,第3个5维向量为:
r3=(1,1,-1,1,-1) T.
按随机超平面算法的步骤2,分别求向量d与r1,r2,r3的点积:
d T r1=-4 < 0,所以s1=0;
d T r2=-2 < 0,所以s2=0;
d T r3=6 > 0,所以s3=1.
故最终的签名s=001,与simhash算法产生的结果是一致的。
从上面的计算过程可以看出,simhash算法其实与随机超平面hash算法是相同的,simhash算法得到的两个签名的汉明距离,可以用来衡量原始向量的夹角。这其实是一种降维技术,将高维的向量用较低维度的签名来表征。衡量两个内容相似度,需要计算汉明距离,这对给定签名查找相似内容的应用来说带来了一些计算上的困难;我想,是否存在更为理想的simhash算法,原始内容的差异度,可以直接由签名值的代数差来表示呢?
3、比较相似度
海明距离: 两个码字的对应比特取值不同的比特数称为这两个码字的海明距离。一个有效编码集中, 任意两个码字的海明距离的最小值称为该编码集的海明距离。举例如下: 10101 和 00110 从第一位开始依次有第一位、第四、第五位不同,则海明距离为 3.
异或: 只有在两个比较的位不同时其结果是1 ,否则结果为 0
对每篇文档根据SimHash 算出签名后,再计算两个签名的海明距离(两个二进制异或后 1 的个数)即可。根据经验值,对 64 位的 SimHash ,海明距离在 3 以内的可以认为相似度比较高。假设对64 位的 SimHash ,我们要找海明距离在 3 以内的所有签名。我们可以把 64 位的二进制签名均分成 4块,每块 16 位。根据鸽巢原理(也成抽屉原理,见组合数学),如果两个签名的海明距离在 3 以内,它们必有一块完全相同。
我们把上面分成的4 块中的每一个块分别作为前 16 位来进行查找。 建立倒排索引。
如果库中有2^34 个(大概 10 亿)签名,那么匹配上每个块的结果最多有 2^(34-16)=262144 个候选结果 (假设数据是均匀分布, 16 位的数据,产生的像限为 2^16 个,则平均每个像限分布的文档数则 2^34/2^16 = 2^(34-16)) ,四个块返回的总结果数为 4* 262144 (大概 100 万)。原本需要比较 10 亿次,经过索引,大概就只需要处理 100 万次了。由此可见,确实大大减少了计算量。
4、示例代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
|
/**
* Function: 注:该示例程序暂不支持中文
* Date: 2013-8-4 下午11:01:45
* @author june: [email protected]
*/
import java.math.BigInteger;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.StringTokenizer;
public class SimHash {
private String tokens;
private BigInteger intSimHash;
private String strSimHash;
private int hashbits = 64 ;
public SimHash(String tokens) {
this .tokens = tokens;
this .intSimHash = this .simHash();
}
public SimHash(String tokens, int hashbits) {
this .tokens = tokens;
this .hashbits = hashbits;
this .intSimHash = this .simHash();
}
HashMap public BigInteger simHash() {
// 定义特征向量/数组
int [] v = new int [ this .hashbits];
// 1、将文本去掉格式后, 分词.
StringTokenizer stringTokens = new StringTokenizer( this .tokens);
while (stringTokens.hasMoreTokens()) {
String temp = stringTokens.nextToken();
// 2、将每一个分词hash为一组固定长度的数列.比如 64bit 的一个整数.
BigInteger t = this .hash(temp);
for ( int i = 0 ; i < this .hashbits; i++) {
BigInteger bitmask = new BigInteger( "1" ).shiftLeft(i);
// 3、建立一个长度为64的整数数组(假设要生成64位的数字指纹,也可以是其它数字),
// 对每一个分词hash后的数列进行判断,如果是1000...1,那么数组的第一位和末尾一位加1,
// 中间的62位减一,也就是说,逢1加1,逢0减1.一直到把所有的分词hash数列全部判断完毕.
if (t.and(bitmask).signum() != 0 ) {
// 这里是计算整个文档的所有特征的向量和
// 这里实际使用中需要 +- 权重,而不是简单的 +1/-1,
v[i] += 1 ;
} else {
v[i] -= 1 ;
}
}
}
BigInteger fingerprint = new BigInteger( "0" );
StringBuffer simHashBuffer = new StringBuffer();
for ( int i = 0 ; i < this .hashbits; i++) {
// 4、最后对数组进行判断,大于0的记为1,小于等于0的记为0,得到一个 64bit 的数字指纹/签名.
if (v[i] >= 0 ) {
fingerprint = fingerprint.add( new BigInteger( "1" ).shiftLeft(i));
simHashBuffer.append( "1" );
} else {
simHashBuffer.append( "0" );
}
}
this .strSimHash = simHashBuffer.toString();
System.out.println( this .strSimHash + " length " + this .strSimHash.length());
return fingerprint;
}
private BigInteger hash(String source) {
if (source == null || source.length() == 0 ) {
return new BigInteger( "0" );
} else {
char [] sourceArray = source.toCharArray();
BigInteger x = BigInteger.valueOf((( long ) sourceArray[ 0 ]) << 7 );
BigInteger m = new BigInteger( "1000003" );
BigInteger mask = new BigInteger( "2" ).pow( this .hashbits).subtract( new BigInteger( "1" ));
for ( char item : sourceArray) {
BigInteger temp = BigInteger.valueOf(( long ) item);
x = x.multiply(m).xor(temp).and(mask);
}
x = x.xor( new BigInteger(String.valueOf(source.length())));
if (x.equals( new BigInteger( "-1" ))) {
x = new BigInteger( "-2" );
}
return x;
}
}
public int hammingDistance(SimHash other) {
BigInteger x = this .intSimHash.xor(other.intSimHash);
int tot = 0 ;
// 统计x中二进制位数为1的个数
// 我们想想,一个二进制数减去1,那么,从最后那个1(包括那个1)后面的数字全都反了,对吧,然后,n&(n-1)就相当于把后面的数字清0,
// 我们看n能做多少次这样的操作就OK了。
while (x.signum() != 0 ) {
tot += 1 ;
x = x.and(x.subtract( new BigInteger( "1" )));
}
return tot;
}
public int getDistance(String str1, String str2) {
int distance;
if (str1.length() != str2.length()) {
distance = - 1 ;
} else {
distance = 0 ;
for ( int i = 0 ; i < str1.length(); i++) {
if (str1.charAt(i) != str2.charAt(i)) {
distance++;
}
}
}
return distance;
}
public List subByDistance(SimHash simHash, int distance) {
// 分成几组来检查
int numEach = this .hashbits / (distance + 1 );
List characters = new ArrayList();
StringBuffer buffer = new StringBuffer();
int k = 0 ;
for ( int i = 0 ; i < this .intSimHash.bitLength(); i++) {
// 当且仅当设置了指定的位时,返回 true
boolean sr = simHash.intSimHash.testBit(i);
if (sr) {
buffer.append( "1" );
} else {
buffer.append( "0" );
}
if ((i + 1 ) % numEach == 0 ) {
// 将二进制转为BigInteger
BigInteger eachValue = new BigInteger(buffer.toString(), 2 );
System.out.println( "----" + eachValue);
buffer.delete( 0 , buffer.length());
characters.add(eachValue);
}
}
return characters;
}
public static void main(String[] args) {
String s = "This is a test string for testing" ;
SimHash hash1 = new SimHash(s, 64 );
System.out.println(hash1.intSimHash + " " + hash1.intSimHash.bitLength());
hash1.subByDistance(hash1, 3 );
s = "This is a test string for testing, This is a test string for testing abcdef" ;
SimHash hash2 = new SimHash(s, 64 );
System.out.println(hash2.intSimHash + " " + hash2.intSimHash.bitCount());
hash1.subByDistance(hash2, 3 );
s = "This is a test string for testing als" ;
SimHash hash3 = new SimHash(s, 64 );
System.out.println(hash3.intSimHash + " " + hash3.intSimHash.bitCount());
hash1.subByDistance(hash3, 4 );
System.out.println( "============================" );
int dis = hash1.getDistance(hash1.strSimHash, hash2.strSimHash);
System.out.println(hash1.hammingDistance(hash2) + " " + dis);
int dis2 = hash1.getDistance(hash1.strSimHash, hash3.strSimHash);
System.out.println(hash1.hammingDistance(hash3) + " " + dis2);
//通过Unicode编码来判断中文
/*String str = "中国chinese" ;
for ( int i = 0 ; i < str.length(); i++) {
System.out.println(str.substring(i, i + 1 ).matches( "[\\u4e00-\\u9fbb]+" ));
}*/
}
}
|
5、适用场景:
simHash在短文本的可行性:
测试相似文本的相似度与汉明距离
测试文本:20个城市名作为词串:北京,上海,香港,深圳,广州,台北,南京,大连,苏州,青岛,无锡,佛山,重庆,宁波,杭州,成都,武汉,澳门,天津,沈阳
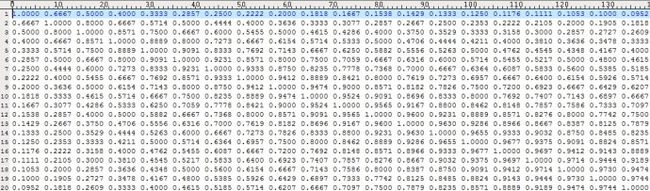
相似度矩阵:
simHash码:
勘误:0.667, Hm:13 是对比的msg 1与2。
可见:相似度在0.8左右的Hamming距离为7,只有相似度高到0.9412,Hamming距离才近到4,此时,反观Google对此算法的应用场景:网页近重复。
镜像网站、内容复制、嵌入广告、计数改变、少量修改。
以上原因对于长文本来说造成的相似度都会比较高,而对于短文本来说,如何处理海量数据的相似度文本更为合适的?
测试短文本(长度在8个中文字符~45个中文字符之间)相似性的误判率如下图所示:
REF:
1、simHash 简介以及java实现
http://blog.sina.com.cn/s/blog_4f27dbd501013ysm.html
2、对simhash算法的一些思考
http://2588084.blog.51cto.com/2578084/558873
3、Simhash算法原理和网页查重应用
http://blog.sina.com.cn/s/blog_72995dcc010145ti.html
4、其它
http://www.cnblogs.com/zhengyun_ustc/archive/2012/06/12/sim.html
http://tech.uc.cn/?p=1086
http://jacoxu.com/?p=369 simHash是否适合短文本的相似文本匹配
https://github.com/sing1ee/simhash-java