Leetcode 热题100

1.两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例: nums = [2, 7, 11, 15], target = 9
	因为 nums[0] + nums[1] = 2 + 7 = 9
	所以返回 [0, 1]

思路：减法

每次判断差值是否在数组中，如果存在还需要判断是否重复。

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums)):
            if target-nums[i] in nums:
                ind = nums.index(target-nums[i])
                if ind != i:
                    return [i,ind]
        return []

以上方法效率很低，可以使用辅助空间，建立一个哈希表（键为数组中的数字，值为对应位置），依然判断差值是否在哈希表中，如果存在，可以直接返回。

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        res = {}
        for i in range(len(nums)):
            if target-nums[i] not in res:
                res[nums[i]] = i
            else:
                return [res[target-nums[i]],i]
        return []

2. 两数相加

给出两个 非空 的链表用来表示两个非负的整数。其中，它们各自的位数是按照 逆序 的方式存储的，并且它们的每个节点只能存储 一位 数字。
如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：
	输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
	输出：7 -> 0 -> 8
	原因：342 + 465 = 807

思路：进位

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        head = ListNode(None)
        p = head
        c = 0
        while l1 or l2 or c:
            if l1:
                c += l1.val
                l1 = l1.next
            if l2:
                c += l2.val
                l2 = l2.next
            p.next = ListNode(c % 10)
            p = p.next
            c = c // 10
        return head.next

3. 无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:
	输入: "abcabcbb"
	输出: 3 
	解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
示例 2:
	输入: "bbbbb"
	输出: 1
	解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
示例 3:
	输入: "pwwkew"
	输出: 3
	解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

思路：字典，更新指针

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        if not s:
            return 0
        if len(s) == 1:
            return 1
        p = 0
        dic = {}
        max_ = 0
        for i in range(len(s)):
            if (s[i] in dic) and (dic[s[i]] >= p):
                p = dic[s[i]]+1
            dic[s[i]] = i
            max_ = max(max_, i-p+1)
        return max_

4. 寻找两个有序数组的中位数

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。

示例 1:
	nums1 = [1, 3]
	nums2 = [2]
	则中位数是 2.0
示例 2:
	nums1 = [1, 2]
	nums2 = [3, 4]
	则中位数是 (2 + 3)/2 = 2.5

思路：分块，考虑临界值

官方的递归法思路最清晰：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-shu-b/

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        A,B = nums1,nums2
        m,n = len(A),len(B)
        if m>n:
            A,B = B,A
            m,n = n,m
        imin = 0
        imax = m
        while imin<=imax:
            i = (imin+imax)//2
            j = (m+n)//2-i
            if i>0 and j<n and A[i-1]>B[j]:
                imax = i-1
            elif i<m and j>0 and B[j-1]>A[i]:
                imin = i+1
            else:
                if i == 0:
                    left = B[j-1]
                elif j == 0:
                    left = A[i-1]
                else:
                    left = max(A[i-1],B[j-1])
                
                if i == m:
                    right = B[j]
                elif j == n:
                    right = A[i]
                else:
                    right = min(A[i],B[j])
                
                if (m+n)%2 == 1:
                    return right
                else:
                    return (left+right)/2.0

5.最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：
	输入: "babad"
	输出: "bab"
	注意: "aba" 也是一个有效答案。
示例 2：
	输入: "cbbd"
	输出: "bb"

思路：马拉车算法

https://editor.csdn.net/md/?articleId=100672168

class Solution:
    def longestPalindrome(self, s: str) -> str:
        ss = '$#'+'#'.join(s)+'#%'
        l = len(ss)
        p = [0]*l
        max_ = 0
        id_ = 0
        for i in range(1,l-1):
            if max_ > i:
                p[i] = min(max_-i,p[2*id-i])
            else:
                p[i] = 1
            while ss[i+p[i]]==ss[i-p[i]]:
                p[i] += 1
            if i+p[i]>max_:
                max_ = i+p[i]
                id = i
        maxr = max(p)
        ind = p.index(maxr)
        res = ss[ind-maxr+1:ind+maxr].replace('#','')
        return res

10.正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

示例 1:
	输入:
	s = "aa"
	p = "a"
	输出: false
	解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
	输入:
	s = "aa"
	p = "a*"
	输出: true
	解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
	输入:
	s = "ab"
	p = ".*"
	输出: true
	解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。
示例 4:
	输入:
	s = "aab"
	p = "c*a*b"
	输出: true
	解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
	输入:
	s = "mississippi"
	p = "mis*is*p*."
	输出: false

思路1：回溯

这个思路比较简单，考虑第二个字符是否为 '*' 即可。
（牛客通过，Leetcode超时）

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        if not s and not p:
            return True
        if len(s)>0 and not p:
            return False
        
        if len(p)>1 and p[1]=='*':
            if len(s)>0 and (s[0]==p[0] or p[0]=='.'):
                return self.isMatch(s,p[2:]) or self.isMatch(s[1:],p[2:]) or self.isMatch(s[1:],p)
            else:
                return self.isMatch(s,p[2:])
        elif len(s)>0 and (s[0]==p[0] or p[0]=='.'):
            return self.isMatch(s[1:],p[1:])
        else:
            return False

仔细分析后可以发现，其实这样做self.isMatch(s[1:],p[2:])是不需要考虑的，因为它实际上可以包含在self.isMatch(s[1:],p)之中（即，匹配1次可以包含在匹配多次中），如果字符串较短时不会超时，但是如果遇到长字符串，重复计算一定会超时，所以考虑删去这一行，重新提交即可通过。（虽然用时较长）

思路二：动态规划

这个思路，有请乔碧萝殿下为我们解答，优秀噢！
https://leetcode-cn.com/problems/regular-expression-matching/solution/dong-tai-gui-hua-zen-yao-cong-0kai-shi-si-kao-da-b/

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        dp = [[False]*(len(p)+1) for _ in range(len(s)+1)]
        dp[0][0] = True
        for i in range(2,len(p)+1):
            dp[0][i] = p[i-1] == '*' and dp[0][i-2]
        for i in range(1,len(s)+1):
            for j in range(1,len(p)+1):
                if p[j-1] == s[i-1] or p[j-1] == '.':
                    dp[i][j] = dp[i-1][j-1]
                elif j>1 and p[j-1] == '*':
                    if p[j-2] == s[i-1] or p[j-2] == '.':
                        dp[i][j] = dp[i-1][j] or dp[i][j-2]
                    elif p[j-2] != s[i-1]:
                        dp[i][j] = dp[i][j-2]
        return dp[-1][-1]

需要注意的点是：1.初始化矩阵时，dp[0][0] = True，第一列都为False，第一行要单独考虑，比如p = 'a*'时为True的情况；2.和前一种思路一样，遇到'*'时，匹配单个字符的情况包含在匹配多个字符的情况中，所以可以不必考虑；3.'*'中的两种情况注意判断顺序；

11. 盛最多水的容器

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2。

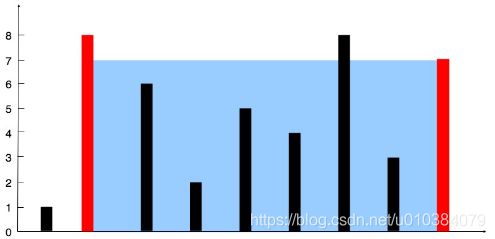
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:
	输入: [1,8,6,2,5,4,8,3,7]
	输出: 49

思路：双指针

首尾两个指针；每次向内移动短的指针。
这个思路我认为解释的最直观的是这位同学：
https://leetcode-cn.com/problems/container-with-most-water/solution/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/

至于两指针长度相等的情况，移动任何哪一个结果都一样，因为只有两种情况：第一种，两个指针之间不是最大面积，移动哪一个都可以；第二种，保留两者之一，那么最大面积一定是这两个指针构成的，因为另一根指针无论比这两个指针长或短，高度总是由短的确定，面积都不可能比这两个指针够成的面积大。
所以下面的判断条件height[i]替换为<=也可以通过所有测试用例。

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_ = 0
        i = 0
        j = len(height)-1
        while i < j:
            max_ = max(max_, min(height[i],height[j])*(j-i))
            if height[i]<height[j]:
                i += 1
            else:
                j -= 1
        return max_

15. 三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。
注意：答案中不可以包含重复的三元组。

示例：
	给定数组 nums = [-1, 0, 1, 2, -1, -4]，
	满足要求的三元组集合为：[ [-1, 0, 1],  [-1, -1, 2] ]

思路：双指针

吴彦祖同学解释的很清楚。
https://leetcode-cn.com/problems/3sum/solution/pai-xu-shuang-zhi-zhen-zhu-xing-jie-shi-python3-by/

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        if not nums or len(nums)<3:
            return []
        n = len(nums)
        nums.sort()
        res = []
        for i in range(n):
            if nums[i]>0:
                break
            elif i>0 and nums[i] == nums[i-1]:
                continue
            else:
                l, r = i+1, n-1
                while l<r:
                    sum_ = nums[i]+nums[l]+nums[r]
                    if sum_>0:
                        r -= 1
                    elif sum_<0:
                        l +=1
                    else:
                        res.append([nums[i],nums[l],nums[r]])
                        while l<r and nums[l+1] == nums[l]:
                            l += 1
                        while l<r and nums[r-1] == nums[r]:
                            r -= 1
                        l += 1
                        r -= 1
        return res

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:
输入：“23”
输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
说明:尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

思路：DFS（回溯）

class Solution:     
    def letterCombinations(self, digits: str) -> List[str]:
        letter= {
            '2':['a', 'b', 'c'], 
            '3':['d', 'e', 'f'],
            '4':['g', 'h', 'i'],
            '5':['j', 'k', 'l'],
            '6':['m', 'n', 'o'],
            '7':['p', 'q', 'r', 's'],
            '8':['t', 'u', 'v'],
            '9':['w', 'x', 'y', 'z']}
        def dfs(string, digits):
            if not digits:
                res.append(string)
            else:
                for i in letter[digits[0]]:
                    dfs(string+i, digits[1:])
        res = []
        if digits:
            dfs('', digits)
        return res

19. 删除链表的倒数第N个节点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：
	给定一个链表: 1->2->3->4->5, 和 n = 2.
	当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：给定的 n 保证是有效的。

思路：双指针

加入一个root节点，以防删除头指针的情况。
这里的动画可以完美诠释这个方法
https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/solution/dong-hua-tu-jie-leetcode-di-19-hao-wen-ti-shan-chu/

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        root = ListNode(0)
        root.next = head
        p1,p2 = root,head
        for _ in range(n):
            p2 = p2.next
        while p2:
            p1 = p1.next
            p2 = p2.next
        p1.next = p1.next.next
        return root.next

20. 有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串，判断字符串是否有效。

有效字符串需满足：
	左括号必须用相同类型的右括号闭合。
	左括号必须以正确的顺序闭合。
	注意空字符串可被认为是有效字符串。

思路：栈

class Solution:
    def isValid(self, s: str) -> bool:
        l = ['(', '[', '{']
        r = [')', ']', '}']
        temp = []
        for i in s:
            if i in l:
                temp.append(i)
            else:
                if not temp or r.index(i) != l.index(temp.pop()):
                    return False
        if temp:
            return False
        return True

21. 合并两个有序链表

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：
	输入：1->2->4, 1->3->4
	输出：1->1->2->3->4->4

思路1：递归

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        if not l2:
            return l1
        if not l1:
            return l2
        if l1.val<l2.val:
            l1.next = self.mergeTwoLists(l1.next,l2)
            return l1
        else:
            l2.next = self.mergeTwoLists(l1,l2.next)
        return l2

思路2：迭代

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        root = ListNode(0)
        pre = root
        while l1 and l2:
            if l1.val<l2.val:
                pre.next = l1
                l1 = l1.next
            else:
                pre.next = l2
                l2 = l2.next
            pre = pre.next
        if l1:
            pre.next = l1
        if l2:
            pre.next = l2
        return root.next

22. 括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：
	[ "((()))", "(()())", "(())()", "()(())", "()()()" ]

思路：DFS（回溯）

考虑合法输出：
左括号数小于n时，可以添加左括号；
右括号数小于左括号数时，可以添加右括号；

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        if n <= 0:
            return []
        def generate(s, l, r):
            if len(s) == 2*n:
                res.append(s)
                return
            if l<n:
                generate(s+'(', l+1, r)
            if r<l:
                generate(s+')', l, r+1)
        res = []
        generate('', 0, 0)
        return res

23. 合并K个排序链表

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6

思路：逐一比较（效率很低）

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        root = ListNode(0)
        temp = root
        lists = [i for i in lists if i]
        while lists:
            min_ = lists[0].val
            p = 0
            for i in range(1,len(lists)):
                if lists[i].val<min_:
                    min_ = lists[i].val
                    p = i
            temp.next = lists[p]
            temp = temp.next
            lists[p] = lists[p].next
            lists = [i for i in lists if i]
        return root.next

可以考虑两两合并，分治思想。
参考官方解释，分析各种方法的复杂度！
https://leetcode-cn.com/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode/

31. 下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。
必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
	1,2,3 → 1,3,2
	3,2,1 → 1,2,3
	1,1,5 → 1,5,1

思路：扫描

第一遍从后向前扫描，找到要交换的数字位置（第一个满足nums[i-1]）；
第二遍从后向前扫描，找到被交换的数字位置（第一个满足nums[j]>nums[i-1]）；
交换两个数字nums[i-1], nums[j]；
然后将i到结尾的数字进行升序排列（原序列为降序，只需要两两交换即可）；

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = j = l = len(nums)-1
        while i>0 and nums[i-1]>=nums[i]:
            i -= 1 

        if i>0:
            while j>0 and nums[j]<=nums[i-1]:
                j-=1
            nums[i-1],nums[j] = nums[j],nums[i-1]

        while i<l:
            nums[i],nums[l] = nums[l],nums[i]
            i += 1
            l -= 1

32. 最长有效括号

给定一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:
	输入: "(()"
	输出: 2
	解释: 最长有效括号子串为 "()"
示例 2:
	输入: ")()())"
	输出: 4
	解释: 最长有效括号子串为 "()()"

官方题解：https://leetcode-cn.com/problems/longest-valid-parentheses/solution/zui-chang-you-xiao-gua-hao-by-leetcode/

思路1：动态规划

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if not s:
            return 0
            
        dp = [0]*(len(s))
        for i in range(len(s)):
            if s[i] == ')' and i-1>=0 and s[i-1] == '(':
                if i == 1:
                    dp[i] = 2
                else:
                    dp[i] = dp[i-2]+2
            elif s[i] == ')' and i-1>=0 and  s[i-1] == ')' and i-dp[i-1]-1>=0 and s[i-dp[i-1]-1] == '(':
                dp[i] = dp[i-1] + 2
                if i-dp[i-1]-2>=0:
                    dp[i] += dp[i-dp[i-1]-2]
            else:
                continue
        return max(dp)

思路2：栈

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if not s:
            return 0
        stack = [-1]
        max_ = 0
        for i in range(len(s)):
            if s[i] == '(':
                stack.append(i)
            else:
                stack.pop()
                if not stack:
                    stack.append(i)
                max_ = max(max_, i-stack[-1])
        return max_

思路3：遍历两遍（十分巧妙，速度也最快）

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if not s:
            return 0
        max_ = 0

        left, right =0, 0
        for i in s:
            if i == '(':
                left += 1
            else:
                right += 1
            if left == right:
                max_ = max(max_, 2*left)
            if right>left:
                left, right =0, 0

        left, right =0, 0
        for i in s[::-1]:
            if i == '(':
                left += 1
            else:
                right += 1
            if left == right:
                max_ = max(max_, 2*left)
            if left>right:
                left, right =0, 0
        
        return max_

33. 搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。

示例 1:
	输入: nums = [4,5,6,7,0,1,2], target = 0
	输出: 4
示例 2:
	输入: nums = [4,5,6,7,0,1,2], target = 3
	输出: -1

思路：二分法

思路要清晰：分为左边升序和右边升序两种情况考虑即可！

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if not nums:
            return -1
        p1, p2 = 0, len(nums)-1
        while p1<=p2:
            mid = (p1+p2)//2
            if nums[mid] == target:
                return mid
            elif nums[p1] <= nums[mid]:
                if nums[p1] <= target and nums[mid] > target:
                    p2 = mid - 1
                else:
                    p1 = mid + 1
            else:
                if nums[p2] >= target and nums[mid] < target:
                    p1 = mid +1
                else:
                    p2 = mid -1
        return -1

34. 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值，返回 [-1, -1]。

示例 1:
	输入: nums = [5,7,7,8,8,10], target = 8
	输出: [3,4]
示例 2:
	输入: nums = [5,7,7,8,8,10], target = 6
	输出: [-1,-1]

二分法

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if not nums:
            return [-1,-1]
        l = self.left(nums, target)
        r = self.right(nums, target)
        return [l,r]

    def left(self,nums, target):
        p1, p2 = 0, len(nums)-1
        while p1<=p2:
            mid = (p1+p2)//2
            if nums[mid]>target:
                p2 = mid - 1
            elif nums[mid]<target:
                p1 = mid + 1
            else:
                if mid == 0 or nums[mid-1] != target:
                    return mid
                else:
                    p2 = mid - 1
        return -1
    def right(self,nums, target):
        p1, p2 = 0, len(nums)-1
        while p1<=p2:
            mid = (p1+p2)//2
            if nums[mid]>target:
                p2 = mid - 1
            elif nums[mid]<target:
                p1 = mid + 1
            else:
                if mid == len(nums)-1 or nums[mid+1] != target:
                    return mid
                else:
                    p1 = mid + 1
        return -1

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明：
所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1:
	输入: candidates = [2,3,6,7], target = 7,
	所求解集为:[ [7], [2,2,3] ]
示例 2:
	输入: candidates = [2,3,5], target = 8,
	所求解集为:[ [2,2,2,2], [2,3,3], [3,5] ]

思路：DFS（回溯） + 剪枝

巧妙的剪枝！好好体会一下！
https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        if not candidates:
            return []
        candidates.sort()
        l = len(candidates)
        res = []
        self.dfs(candidates, 0, l, [], res, target)
        return res
    def dfs(self, nums, p, l, path, res, target):
        if target == 0:
            res.append(path[:])
            return
        for i in range(p,l):
            temp = target - nums[i]
            if temp < 0:
                break
            else:
                path.append(nums[i])
                self.dfs(nums, i, l, path, res, temp)
                path.pop()

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

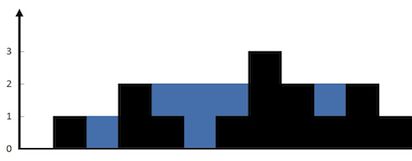
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:
	输入: [0,1,0,2,1,0,1,3,2,1,2,1]
	输出: 6

思路：按行求，按列求，动态规划，双指针

参考详细讲解https://leetcode-cn.com/problems/trapping-rain-water/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-8/

其中动态规划实际上是按列求的优化：

class Solution:
    def trap(self, height: List[int]) -> int:
        if len(height) < 2:
            return 0
        len_ = len(height)
        left = [0]*len_
        right = [0]*len_
        for i in range(1, len_-1):
            left[i] = max(left[i-1], height[i-1])
        for i in range(len_-2, 0, -1):
            right[i] = max(right[i+1], height[i+1])
        
        sum_ = 0
        for i in range(1,len_-1):
            min_ = min(left[i], right[i])
            if min_ > height[i]:
                sum_ += min_-height[i]
        return sum_

46. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:
	输入: [1,2,3]
	输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路：回溯法

两种实现方法：
第一种：比较简单明了

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return []
        if len(nums) == 1:
            return [nums]
        res = []
        for i in range(len(nums)):
            temp = []
            temp = self.permute(nums[:i]+nums[i+1:])
            for j in temp:
                res.append([nums[i]]+j)
        return res

第二种：仔细体会体会

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []
        def backtrack(nums, temp):
            if not nums:
                res.append(temp)
                return
            for i in range(len(nums)):
                backtrack(nums[:i]+nums[i+1:], temp+[nums[i]])
        backtrack(nums,[])
        return res

48. 旋转图像

给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:
	给定 matrix = 
    [ [1,2,3],
	  [4,5,6],
	  [7,8,9] ],
	原地旋转输入矩阵，使其变为:
	[ [7,4,1],
	[8,5,2],
	[9,6,3] ]
示例 2:
	给定 matrix =
	[ [ 5, 1, 9,11],
	  [ 2, 4, 8,10],
	  [13, 3, 6, 7],
	  [15,14,12,16] ], 
	原地旋转输入矩阵，使其变为:
	[ [15,13, 2, 5],
	  [14, 3, 4, 1],
	  [12, 6, 8, 9],
	  [16, 7,10,11] ]

思路1：转置+翻转

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix[0])
        for i in range(n-1):
            for j in range(i+1,n):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        for i in range(n):
            for j in range(n//2):
                matrix[i][j], matrix[i][n-1-j] = matrix[i][n-1-j], matrix[i][j]

思路2：直接旋转

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix[0])
        for i in range(n//2):
            for j in range(n//2 + n%2):
                tmp = matrix[i][j]
                matrix[i][j] = matrix[n-1-j][i]
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j]
                matrix[n-1-i][n-1-j] = matrix[j][n-1-i]
                matrix[j][n-1-i] = tmp

49. 字母异位词分组

给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。

示例:
	输入: ["eat", "tea", "tan", "ate", "nat", "bat"],
	输出: [ ["ate","eat","tea"],
			   ["nat","tan"],
			   ["bat"] ]

说明：
所有输入均为小写字母。
不考虑答案输出的顺序。

哈希表

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        res = {}
        for i in strs:
            k = tuple(sorted(i))
            if k not in res:
                res[k] = [i]
            else:
                res[k].append(i)
        return list(res.values())

53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:
	输入: [-2,1,-3,4,-1,2,1,-5,4],
	输出: 6
	解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶:
如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

55. 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。

示例 1:
	输入: [2,3,1,1,4]
	输出: true
	解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
	输入: [3,2,1,0,4]
	输出: false
	解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

思路1：回溯

即使加了记录当前位置是BAD/GOOD的数组，避免重复的计算，结果依然还是超时。。。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        tmp = [True]*len(nums)
        def jump(nums, p, step):
            if nums[p] >= step:
                return True
            else:
                for i in range(nums[p],0,-1):
                    if not tmp[p+i]:
                        continue
                    res = jump(nums, p+i,step-i)
                    if res:
                        return res
                    tmp[p+i] = False
                return False
        return jump(nums, 0, len(nums)-1)

思路2：贪心

自底向上回溯的改进版本；
从右向左遍历，记录并更新最左边的GOOD位置。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        l = len(nums)
        p = l - 1
        for i in range(l-2,-1,-1):
            if nums[i] >= p-i:
                p = i
        if p == 0:
            return True
        return False

56. 合并区间

给出一个区间的集合，请合并所有重叠的区间。

示例 1:
	输入: [[1,3],[2,6],[8,10],[15,18]]
	输出: [[1,6],[8,10],[15,18]]
	解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
	输入: [[1,4],[4,5]]
	输出: [[1,5]]
	解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

思路：排序合并

这手排序intervals = sorted(intervals, key = lambda x: x[0])很灵性好吧！

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        if not intervals:
            return []
        intervals = sorted(intervals, key = lambda x: x[0])
        res = []
        tmp = intervals[0]
        for i in intervals[1:]:
            if i[0]<=tmp[1]:
                tmp[1] = max(tmp[1],i[1])
            else:
                res.append(tmp)
                tmp = i
        res.append(tmp)
        return res

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

思路：动态规划

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[1]*n]*m
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i-1][j]+dp[i][j-1]
        return dp[-1][-1]

优化：

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [1]*n
        for i in range(1,m):
            for j in range(1,n):
                dp[j] = dp[j-1] + dp[j]
        return dp[-1]

思路1：暴力法

超时！

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        def path(grid, i, j):
            if i == len(grid) or j == len(grid[0]):
                return float('Inf')
            elif i == len(grid)-1 and j == len(grid[0])-1:
                return grid[i][j]
            else:
                return grid[i][j] + min(path(grid, i+1, j),path(grid, i, j+1))
        return path(grid, 0, 0)

思路2：动态规划

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i == 0 and j == 0:
                    continue
                elif i == 0:
                    grid[i][j] += grid[i][j-1]
                elif j == 0:
                    grid[i][j] += grid[i-1][j]
                else:
                    grid[i][j] += min(grid[i-1][j], grid[i][j-1])
        return grid[-1][-1]

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

示例 1：
	输入： 2
	输出： 2
	解释： 有两种方法可以爬到楼顶。
		  1.  1 阶 + 1 阶
		  2.  2 阶

思路：斐波那契数列（easy）

class Solution:
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        p1, p2 = 1, 2
        for i in range(2,n):
            tmp = p2
            p2 += p1
            p1 = tmp
        return p2

72. 编辑距离

https://blog.csdn.net/u010384079/article/details/99603217

二维数组：

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        l1, l2 = len(word1)+1, len(word2)+1
        res = [[0]*(l2) for _ in range(l1)]
        for i in range(l1):
            for j in range(l2):
                if i == 0: res[0][j] = j
                elif j == 0: res[i][0] = i
                else:
                    if word1[i-1] == word2[j-1]:
                        res[i][j] = res[i-1][j-1]
                    else: 
                        res[i][j] = min(res[i-1][j], res[i][j-1], res[i-1][j-1]) + 1
        return res[-1][-1]

75. 颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意: 不能使用代码库中的排序函数来解决这道题。

示例:
	输入: [2,0,2,1,1,0]
	输出: [0,0,1,1,2,2]

进阶：
一个直观的解决方案是使用计数排序的两趟扫描算法。
首先，迭代计算出0、1 和 2 元素的个数，然后按照0、1、2的排序，重写当前数组。
你能想出一个仅使用常数空间的一趟扫描算法吗？

荷兰国旗问题

用三个指针即可，有点东西嗷！

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        p1,p2 = 0,len(nums)-1
        cur = 0
        while cur<=p2:
            if nums[cur] == 0:
                nums[cur], nums[p1] = nums[p1], nums[cur]
                p1 += 1
                cur += 1
            elif nums[cur] == 2:
                nums[cur], nums[p2] = nums[p2], nums[cur]
                p2 -= 1
            else:
                cur += 1

76. 最小覆盖子串

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。

示例：
	输入: S = "ADOBECODEBANC", T = "ABC"
	输出: "BANC"

说明：
如果 S 中不存这样的子串，则返回空字符串 “”。
如果 S 中存在这样的子串，我们保证它是唯一的答案。

思路：滑动窗口算法（emmm）

好好体会！好好学习！
https://leetcode-cn.com/problems/minimum-window-substring/solution/zui-xiao-fu-gai-zi-chuan-by-leetcode-2/

使用相同算法的三道例题：
https://leetcode-cn.com/problems/minimum-window-substring/solution/hua-dong-chuang-kou-suan-fa-tong-yong-si-xiang-by-/

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        if not s or not t:
            return ''
            
        dict_t = {}
        for i in t:
            dict_t[i] = dict_t.get(i,0) + 1
        goal = len(dict_t)

        l, r = 0, 0
        dict_s = {}
        mark = 0
        ans = [float('inf'), 0, 0]
        while r < len(s):
            cha = s[r]
            if cha in dict_t:
                dict_s[cha] = dict_s.get(cha,0) + 1
                if dict_s[cha] == dict_t[cha]:
                    mark += 1
            while l <= r and mark == goal:
                cha = s[l]
                if r-l+1 < ans[0]:
                    ans = [r-l+1, l, r]
                if cha in dict_t:
                    dict_s[cha] -= 1
                    if dict_s[cha] < dict_t[cha]:
                        mark -= 1
                l += 1
            r += 1
        if ans[0] == float('inf'):
            return ''
        return s[ans[1]:ans[2]+1]

78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。

示例:
	输入: nums = [1,2,3]
	输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

思路1：递归

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = [[]]
        for i in nums:
            res += [j + [i] for j in res]
        return res

思路2：回溯（必回！）

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        n = len(nums)
        def backtrack(i, cur):
            res.append(cur)
            for i in range(i,n):
                backtrack(i+1, cur+[nums[i]])
        backtrack(0,[])
        return res

79. 单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:
	board = [ ['A','B','C','E'],
			  ['S','F','C','S'],
		 	  ['A','D','E','E'] ]
	给定 word = "ABCCED", 返回 true.
	给定 word = "SEE", 返回 true.
	给定 word = "ABCB", 返回 false.

思路：DFS（回溯）

实现方法1：

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board)
        n = len(board[0])
        mark = [[False]*n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if self.path(board, m, n, i, j, 0, word, mark):
                    return True
        return False
    def path(self, board, m, n, i, j, index, word, mark):
        if index == len(word):
            return True
        res = False
        if i>=0 and i<m and j>=0 and j<n and board[i][j]==word[index] and not mark[i][j]:
            mark[i][j] = True
            res = self.path(board, m, n, i+1, j, index+1, word, mark) or \
                  self.path(board, m, n, i-1, j, index+1, word, mark) or \
                  self.path(board, m, n, i, j+1, index+1, word, mark) or \
                  self.path(board, m, n, i, j-1, index+1, word, mark)
            if not res:
                mark[i][j] = False
        return res

实现方法2：（使用偏移量数组）

class Solution:
    direction = [(1,0), (-1,0), (0,1), (0,-1)]
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board)
        n = len(board[0])
        mark = [[False]*n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if self.path(board, m, n, i, j, 0, word, mark):
                    return True
        return False
    def path(self, board, m, n, i, j, index, word, mark):
        if index == len(word):
            return True
        if i>=0 and i<m and j>=0 and j<n and board[i][j]==word[index] and not mark[i][j]:
            mark[i][j] = True
            for d in self.direction:
                if self.path(board, m, n, i+d[0], j+d[1], index+1, word, mark):
                    return True
            mark[i][j] = False
        return False

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例:
	输入: [2,1,5,6,2,3]
	输出: 10

思路1：暴力法

搜索每一个可形成的矩形。超时！

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        maxarea = 0
        for i in range(len(heights)):
            minheight = heights[i]
            for j in range(i, len(heights)):
                minheight = min(minheight, heights[j])
                maxarea = max(maxarea, minheight*(j-i+1))
        return maxarea

思路2：分治

神奇的想法，虽然还是会超时。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        def cal(h, start, end):
            if start > end:
                return 0
            minh = start
            for i in range(start,end+1):
                if h[i] < h[minh]:
                    minh = i
            mid = h[minh] * (end-start+1)
            left = cal(h, start, minh-1)
            right = cal(h, minh+1, end)
            return max(mid, left, right)
        return cal(heights, 0, len(heights)-1)

思路3：栈（女少口阿！！）

品！细品！
https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode/
https://blog.csdn.net/Zolewit/article/details/88863970
两个小技巧：
1.初始时把 -1 放入栈顶，方便计算面积值。
2.基于各个高度的最大矩形是在出栈的时候计算的，因此必须要让所有高度都出栈。利用单调栈的性质让其全部出栈，即在原始数组后添一个 0 。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        heights.append(0)
        stack = [-1]
        maxarea = 0
        for i in range(len(heights)):
            while stack[-1]!=-1 and heights[stack[-1]]>heights[i]:
                maxarea = max(maxarea, heights[stack.pop()]*(i-stack[-1]-1)) 
            stack.append(i)
        return maxarea

85. 最大矩形（细品！）

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:
	输入: [ ["1","0","1","0","0"],
		   ["1","0","1","1","1"],
		   ["1","1","1","1","1"],
		   ["1","0","0","1","0"] ]
	输出: 6

显然暴力法尝试每一种可能性会超时！
动态规划柱状图法对暴力法进行优化，优秀；
进一步借助上一题的栈的思想进行柱状图法优化，呕吼；

思想：柱状图 - 栈

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if not matrix:
            return 0
        maxarea = 0
        dp = [0]*len(matrix[0])
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                dp[j] = dp[j]+1 if matrix[i][j]=='1' else 0
            maxarea = max(maxarea, self.cal(dp))
        return maxarea
    def cal(self, lis):
        lis.append(0)
        stack = [-1]
        maxarea = 0
        for i in range(len(lis)):
            while stack[-1]!=-1 and lis[stack[-1]]>=lis[i]:
                maxarea = max(maxarea, lis[stack.pop()]*(i-stack[-1]-1))
            stack.append(i)
        return maxarea

96. 不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:
	输入: 3
	输出: 5
	解释:给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

思路１：动态规划

class Solution:
    def numTrees(self, n: int) -> int:
        res = [1,1]
        for i in range(2,n+1):
            tmp = 0
            for j in range(i):
                tmp += res[j]*res[ｉ-j-1]
            res.append(tmp)
        return res[-1]

思路２：栈（很有用）

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        stack = []
        while stack or root:
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()
            res.append(root.val)
            root = root.right
        return res

98. 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
节点的左子树只包含小于当前节点的数；
节点的右子树只包含大于当前节点的数；
所有左子树和右子树自身必须也是二叉搜索树；

思路：中序遍历（栈）

注意：这种思路有一个问题要考虑，二叉树中是否含有相同值的结点，如果先遍历，然后将其与排序的遍历结果，是无法处理含有相同值的情况的，比如[1, 1]结果应该为False，但先遍历后判断结果却为True。因此考虑用栈的思想，一边遍历一遍判断。

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        pre = -float('inf')
        stack = []
        while stack or root:
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()
            if root.val <= pre:
                return False
            pre = root.val
            root = root.right
        return True

101. 对称二叉树(easy)

102. 二叉树的层次遍历(easy)

104. 二叉树的最大深度(easy)

105. 从前序与中序遍历序列构造二叉树(easy)

114. 二叉树展开为链表

给定一个二叉树，原地将它展开为链表。
例如，给定二叉树

将其展开为：

思路：栈保存右结点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def flatten(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        pre = root
        stack = []
        while stack or pre:
            while pre.left:
                if pre.right:
                    stack.append(pre.right)
                pre.right = pre.left
                pre.left = None
                pre = pre.right
            if pre.right:
                pre = pre.right
            elif stack:
                pre.right = stack.pop()
                pre = pre.right
            else:
                pre = None

121. 买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。

示例 1:
	输入: [7,1,5,3,6,4]
	输出: 5
	解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
	注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

思路：一次遍历

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if not prices:
            return 0
        profit = 0
        min_ = prices[0]
        for i in prices:
            if i > min_:
                profit = max(profit, i-min_)
            else:
                min_ = i
        return profit

124. 二叉树中的最大路径和

给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:
	输入: [1,2,3]
	       1
	      / \
	     2   3
	输出: 6
示例 2:
	输入: [-10,9,20,null,null,15,7]
		   -10
		   / \
		  9  20
		    /  \
		   15   7
	输出: 42

思路：递归（神奇）

https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/solution/er-cha-shu-de-zui-da-lu-jing-he-by-leetcode/

class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        max_ = float('-inf')
        def path(node):
            nonlocal max_
            if not node:
                return 0
            left = max(0, path(node.left))
            right = max(0, path(node.right))
            max_ = max(max_, node.val+left+right)
            return node.val + max(left,right)
        path(root)
        return max_

128. 最长连续序列

给定一个未排序的整数数组，找出最长连续序列的长度。
要求算法的时间复杂度为 O(n)。

示例:
	输入: [100, 4, 200, 1, 3, 2]
	输出: 4
	解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

思路1：排序

这个思路注意一个坑点：重复数字的处理

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        if not nums:
            return 0
        nums.sort()
        max_ = 1
        cur = 1
        for i in range(1,len(nums)):
            if nums[i] != nums[i-1]:
                if nums[i] == nums[i-1] + 1:
                    cur += 1
                else:
                    max_ = max(max_, cur)
                    cur = 1
        return max(max_, cur)

思路2：暴力法的优化（时间复杂度O(n) ）

思路太强了！
https://leetcode-cn.com/problems/longest-consecutive-sequence/solution/dong-tai-gui-hua-python-ti-jie-by-jalan/

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        if not nums:
            return 0
        dic = {}
        max_ = 0
        for i in nums:
            if i not in dic:
                left = dic.get(i-1, 0)
                right = dic.get(i+1, 0)
                cur = 1+left+right
                max_ = max(max_, cur)
                dic[i] = dic[i-left] = dic[i+right] =cur
        return max_

136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
说明：你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:
	输入: [2,2,1]
	输出: 1
示例 2:
	输入: [4,1,2,1,2]
	输出: 4

思路：异或

常规思路需要借助辅助空间，异或可不使用辅助空间

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        for i in nums[1:]:
            nums[0] ^= i
        return nums[0]

139. 单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明：
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例 1：
	输入: s = "leetcode", wordDict = ["leet", "code"]
	输出: true
	解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2：
	输入: s = "applepenapple", wordDict = ["apple", "pen"]
	输出: true
	解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
	注意你可以重复使用字典中的单词。
示例 3：
	输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
	输出: false

思路：动态规划！！！

暴力法和暴力法的记忆优化都会超时；
动态规划的思路好厉害噢：
https://leetcode-cn.com/problems/word-break/solution/dan-ci-chai-fen-by-leetcode/

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        dp = [False]*(len(s)+1)
        dp[0] = True
        for i in range(1,len(s)+1):
            for j in range(0,i):
                if dp[j] and s[j:i] in wordDict:
                    dp[i] = True
                    break
        return dp[-1]

141. 环形链表

是否存在环

思路：双指针

142. 环形链表 II

环的入环结点

思路：双指针

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        p1 = p2 = head
        while True:
            if not p2 or not p2.next:
                return
            p1 = p1.next
            p2 = p2.next.next
            if p1 == p2:
                break
        p2 = head
        while p1 != p2:
            p1 = p1.next
            p2 = p2.next
        return p1

146. LRU缓存机制

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

示例:
	LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
	cache.put(1, 1);
	cache.put(2, 2);
	cache.get(1);       // 返回  1
	cache.put(3, 3);    // 该操作会使得密钥 2 作废
	cache.get(2);       // 返回 -1 (未找到)
	cache.put(4, 4);    // 该操作会使得密钥 1 作废
	cache.get(1);       // 返回 -1 (未找到)
	cache.get(3);       // 返回  3
	cache.get(4);       // 返回  4

思路1：有序字典OrderedDict

思路2：双向链表 + 字典

https://leetcode-cn.com/problems/lru-cache/solution/lru-huan-cun-ji-zhi-by-leetcode/
官方的代码思路更清晰；
另外注意一个坑，如果put相同key的密钥时，需要更新相应的value，所以将不同的功能拆分成不同函数更为清晰。

class Node:
    def __init__(self, key, val):
        self.key = key
        self.val = val
        self.pre = None
        self.nxt = None
class LRUCache:
    def __init__(self, capacity: int):
        self.size = 0
        self.capacity = capacity
        self.dic = {}
        self.start = Node(0, 0)
        self.end = Node(0, 0)
        self.start.nxt = self.end
        self.end.pre = self.start

    def get(self, key: int) -> int:
        if key in self.dic:
            node = self.dic[key]
            node.pre.nxt = node.nxt
            node.nxt.pre = node.pre
            self.start.nxt.pre = node
            node.pre = self.start
            node.nxt = self.start.nxt
            self.start.nxt = node
            return node.val
        else:
            return -1
    def put(self, key: int, value: int) -> None:
        node = self.dic.get(key)
        if node:
            node.val= value
            node.pre.nxt = node.nxt
            node.nxt.pre = node.pre
            self.start.nxt.pre = node
            node.pre = self.start
            node.nxt = self.start.nxt
            self.start.nxt = node
        else:
            node = Node(key, value)
            self.dic[key] = node
            self.start.nxt.pre = node
            node.pre = self.start
            node.nxt = self.start.nxt
            self.start.nxt = node
            self.size += 1
            if self.size > self.capacity:
                node = self.end.pre
                del self.dic[node.key]
                node.pre.nxt = self.end
                self.end.pre = node.pre
                self.size -= 1

148. 排序链表

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例 1:
	输入: 4->2->1->3
	输出: 1->2->3->4
示例 2:
	输入: -1->5->3->4->0
	输出: -1->0->3->4->5

思路：归并排序

class Solution:
    def sortList(self, head: ListNode) -> ListNode:
        if not head or not head.next:
            return head
        p1, p2 = head, head.next
        while p2 and p2.next:
            p1 = p1.next
            p2 = p2.next.next
        mid = p1.next
        p1.next = None
        left = self.sortList(head)
        right = self.sortList(mid)
        return self.mergesort(left,right)
    def mergesort(self, node1, node2):
        root = ListNode(0)
        tmp = root
        while node1 and node2:
            if node1.val < node2.val:
                tmp.next = node1
                node1 = node1.next
            else:
                tmp.next = node2
                node2 = node2.next
            tmp = tmp.next
        tmp.next = node1 if node1 else node2
        return root.next

152. 乘积最大子序列

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

示例 1:
	输入: [2,3,-2,4]
	输出: 6
	解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
	输入: [-2,0,-1]
	输出: 0
	解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

思路：动态规划！

同时维护最大值和最小值，遇到负数先交换再维护！

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        res = float('-inf')
        max_ = min_ = 1
        for i in nums:
            if i < 0:
                max_, min_ = min_, max_
            max_ = max(max_*i, i)
            min_ = min(min_*i, i)
            res = max(max_, res)
        return res

155. 最小栈（easy）

160. 相交链表

编写一个程序，找到两个单链表相交的起始节点。

双指针法（改进版）

原始思路是先统计两个链表长度，让长的链表先前进差值个长度，然后逐步向后直到两指针的节点相等。改进版不用使长链表先前进，直接让两链表首尾相连以及尾首相连。
踩坑了！：判断条件不能使是if pA.next，因为这样对于没有交点的情况会无限循环下去，而判断if pA没有交点的情况会在遍历所有之后None == None就会跳出循环！

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        pA, pB = headA, headB
        while pA != pB:
            pA = pA.next if pA else headB
            pB = pB.next if pB else headA
        return pA