排序八卦炉之归并、计数

1.归并排序

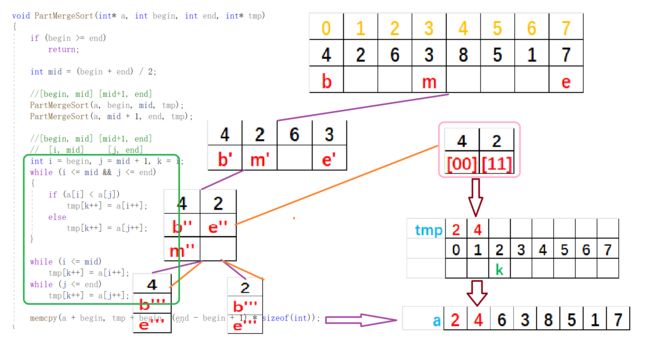
1.1初识代码

//归并排序 时间复杂度：O(N*logN)   空间复杂度：O(N)
void PartMergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
		return;

	int mid = (begin + end) / 2;

	//[begin, mid] [mid+1, end] 
	PartMergeSort(a, begin, mid, tmp);
	PartMergeSort(a, mid + 1, end, tmp);

	//[begin, mid] [mid+1, end]
	//  [i, mid]     [j, end]
	int i = begin, j = mid + 1, k = i;
	while (i <= mid && j <= end)
	{
		if (a[i] < a[j])
			tmp[k++] = a[i++];
		else
			tmp[k++] = a[j++];
	}

	while (i <= mid)
		tmp[k++] = a[i++];
	while (j <= end)
		tmp[k++] = a[j++]; 
	
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	//void PartMergeSort(int* a, int begin, int end, int* tmp);
	PartMergeSort(a, 0, n - 1, tmp);

	free(tmp);
}

1.2代码分析

1.3复杂度

时间复杂度：O(N*logN) 空间复杂度：O(N)
此类情况已讲过多次，此处不再赘述。

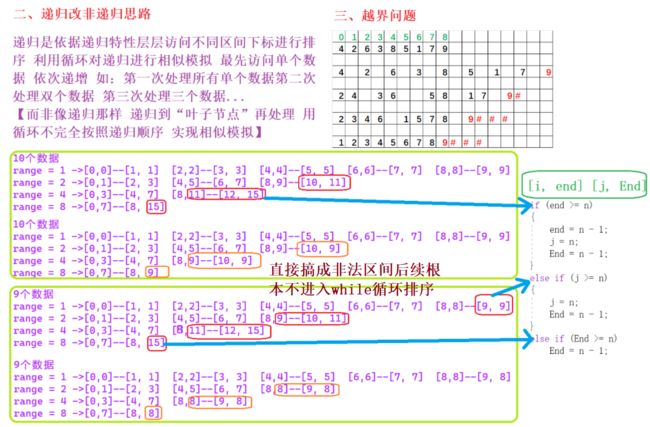
1.4非递归版本1.0

所谓的递归改非递归我们在讲快排时就涉及到过，无非就是通过递归的特性，可以在不断地调用同一函数期间传不同参数，从而达到“分而治之”的效果。上文中快排改非递归用到的栈模拟实现递归，也就是运用了栈“先入后出”的特性【用队列也行 只不过更加麻烦】 而在归并排序想要用非递归实现 是一件更为复杂的事情，需要考虑的更全面。

1.初识代码

void MergeSort_NonRecursion1(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	int range = 1;
	while (range < n)
	{
		printf("range = %d ->", range);
		for (int index = 0; index < n; index += 2 * range)
		{
			int i = index, k = i,  end = index + range - 1;
			int j = index + range, End = index + 2 * range - 1;
			
			//修正边界
			if (end >= n)
			{
				end = n - 1;
				j = n;
				End = n - 1;
			}
			else if (j >= n)
			{
				j = n;
				End = n - 1;
			}
			else if (End >= n)
				End = n - 1;
			printf("[%d,%d]--[%d, %d]  ", i, end, j, End);
			//数据排序
			while (i <= end && j <= End)
			{
				if (a[i] < a[j])
					tmp[k++] = a[i++];
				else
					tmp[k++] = a[j++];
			}
			while (i <= end)
				tmp[k++] = a[i++];
			while (j <= End)
				tmp[k++] = a[j++];
		}
		printf("\n");
		memcpy(a, tmp, sizeof(int) * n);
		range *= 2;
	}

	free(tmp);
}

2.代码分析

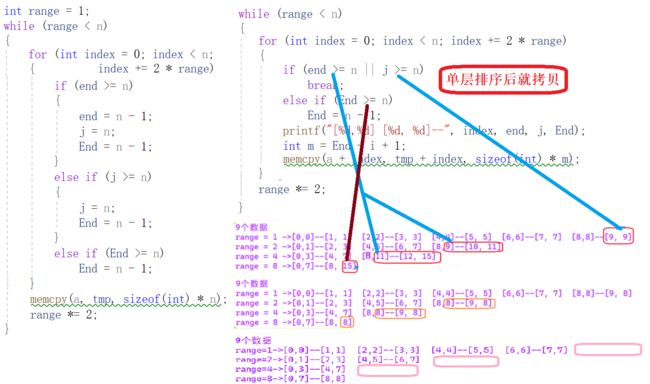
1.5非递归版本2.0

1.初识代码

void MergeSort_NonRecursion2(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	int range = 1;
	while (range < n)
	{
		printf("range=%d->", range);
		for (int index = 0; index < n; index += 2 * range)
		{
			int i = index, k = i, end = index + range - 1;
			int j = index + range, End = index + 2 * range - 1;
            if (end >= n || j >= n)
				break;
			else if (End >= n)
				End = n - 1;
			printf("[%d,%d]--[%d,%d]  ", i, end, j, End);
			int m = End - i + 1;
			while (i <= end && j <= End)
			{
				if (a[i] < a[j])
					tmp[k++] = a[i++];
				else
					tmp[k++] = a[j++];
			}
            while (i <= end)
				tmp[k++] = a[i++];
			while (j <= End)
				tmp[k++] = a[j++];
			memcpy(a + index, tmp + index, sizeof(int) * m);
		}
		printf("\n");
		range *= 2;
	}
	free(tmp);
}

2.代码分析

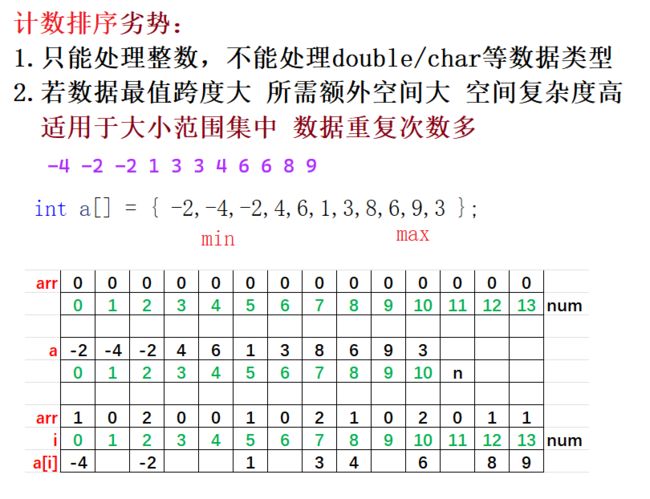
2.计数排序

2.1初始代码

//计数排序  时间复杂度：O(max(num, N)) 空间复杂度：O(num）
void CountSort(int* a, int n)
{
	//确定最值
	int min = a[0], max = a[0];
	for (int i = 1; i < n; ++i)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	int num = max - min + 1;  //最多有N个"连续"的数据
	//开空间
	int* arr = (int*)malloc(sizeof(int) * num);
	if (arr == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	memset(arr, 0, sizeof(int) * num);

	//a的数据映射到arr的下标 arr的值存储对应数据出现次数
	for (int i = 0; i < n; ++i)
		arr[a[i] - min]++;
	for (int i = 0, j = 0; i < num; ++i)
	{
		while (arr[i]--)
			a[j++] = i + min;
	}
}

2.2代码分析