利用ceres库在激光SLAM中添加强度代价函数——来自IntensitySLAM

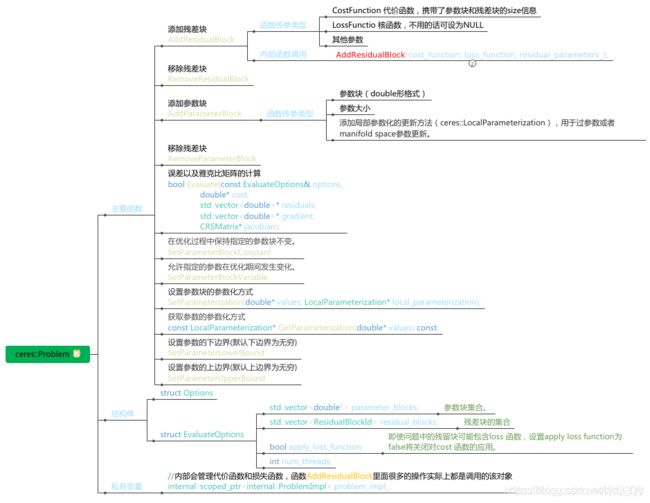
ceres库总览

雷达参数定义

lidar::Lidar::Lidar(){
}
//激光线数
void lidar::Lidar::setLines(double num_lines_in){
    num_lines=num_lines_in;
}
//垂直方向俯仰角度
void lidar::Lidar::setVerticalAngle(double vertical_angle_in){
    vertical_angle = vertical_angle_in;
}
//垂直方向分辨率
void lidar::Lidar::setVerticalResolution(double vertical_angle_resolution_in){
    vertical_angle_resolution = vertical_angle_resolution_in;
}
//扫描周期时间
void lidar::Lidar::setScanPeriod(double scan_period_in){
    scan_period = scan_period_in;
}
//最大距离
void lidar::Lidar::setMaxDistance(double max_distance_in){
  max_distance = max_distance_in;
}
//最小距离
void lidar::Lidar::setMinDistance(double min_distance_in){
  min_distance = min_distance_in;
}

参数初始化

void OdomEstimationClass::init(lidar::Lidar lidar_param){
    //init local map
    //角点
    laserCloudCornerMap = pcl::PointCloud<pcl::PointXYZI>::Ptr(new pcl::PointCloud<pcl::PointXYZI>());
    //平面点
    laserCloudSurfMap = pcl::PointCloud<pcl::PointXYZI>::Ptr(new pcl::PointCloud<pcl::PointXYZI>());
    //所有特征点
    laserCloudDisMap = pcl::PointCloud<pcl::PointXYZI>::Ptr(new pcl::PointCloud<pcl::PointXYZI>());
    //downsampling size 下采样尺寸
    downSizeFilterEdge.setLeafSize(0.4, 0.4, 0.4);
    downSizeFilterSurf.setLeafSize(0.8, 0.8, 0.8);
    downSizeFilterDis.setLeafSize(0.4, 0.4, 0.4);

    //kd-tree
    kdtreeEdgeMap = pcl::KdTreeFLANN<pcl::PointXYZI>::Ptr(new pcl::KdTreeFLANN<pcl::PointXYZI>());
    kdtreeSurfMap = pcl::KdTreeFLANN<pcl::PointXYZI>::Ptr(new pcl::KdTreeFLANN<pcl::PointXYZI>());
    kdtreeDisMap = pcl::KdTreeFLANN<pcl::PointXYZI>::Ptr(new pcl::KdTreeFLANN<pcl::PointXYZI>());
    //里程计初值为单位阵
    odom = Eigen::Isometry3d::Identity();
    last_odom = Eigen::Isometry3d::Identity();
    max_lidar_distance = lidar_param.max_distance * 0.85;
    optimization_count=12;
}

通过ceres库进行优化并将点添加到地图中

void OdomEstimationClass::updatePointsToMap(const pcl::PointCloud<pcl::PointXYZI>::Ptr& edge_in, const pcl::PointCloud<pcl::PointXYZI>::Ptr& surf_in){

    if(optimization_count>4)
        optimization_count--;
    Eigen::Isometry3d odom_prediction = odom * last_odom.inverse() * odom;

    last_odom = odom;
    odom = odom_prediction;
    normalizeIsometry(odom);//把旋转部分取出进行四元数单位化再赋值给矩阵的旋转部分
    normalizeIsometry(last_odom);

    q_w_curr = Eigen::Quaterniond(odom.rotation());
    t_w_curr = odom.translation();

    pcl::PointCloud<pcl::PointXYZI>::Ptr downsampledEdgeCloud(new pcl::PointCloud<pcl::PointXYZI>());
    pcl::PointCloud<pcl::PointXYZI>::Ptr downsampledSurfCloud(new pcl::PointCloud<pcl::PointXYZI>());
    pcl::PointCloud<pcl::PointXYZI>::Ptr downsampledDisCloud(new pcl::PointCloud<pcl::PointXYZI>());
    //下采样到地图中
    downSamplingToMap(edge_in,downsampledEdgeCloud,surf_in,downsampledSurfCloud, downsampledDisCloud);
    pcl::PointCloud<pcl::PointXYZI>::Ptr tmpcloudptr_1(new pcl::PointCloud<pcl::PointXYZI>());
    for(int i=0;i<downsampledDisCloud->points.size();i++)
        tmpcloudptr_1->push_back(downsampledDisCloud->points[i]);
    if(laserCloudCornerMap->points.size()>10 && laserCloudSurfMap->points.size()>50){
        kdtreeEdgeMap->setInputCloud(laserCloudCornerMap);
        kdtreeSurfMap->setInputCloud(laserCloudSurfMap);
        kdtreeDisMap->setInputCloud(laserCloudDisMap);

        for (int iterCount = 0; iterCount < optimization_count; iterCount++){//迭代12次
            ceres::LossFunction *loss_function = new ceres::HuberLoss(0.1);//损失函数 用于去除异常值
            // 残差大于0.1的点 ,则权重降低,具体效果看上面的公式. 小于0.1 则认为正常,不做特殊的处理 s s<0.1 2(sqrt(s+1)-1)
            //problem类就是代表者具有双边约束的最小二乘问题
            //为了创建一个最小二乘问题,需要使用
            //Problem::AddResidalBlock() 添加残差模块
            //Problem::AddParameterBlock() 添加参数模块
            //先声明一个ceres::Problem::Options,然后再用Options初始化problem
            ceres::Problem::Options problem_options;
            ceres::Problem problem(problem_options);
            //Problem::AddParameterBlock() 添加参数模块
            //表示位姿增量double parameters[7] = {0, 0, 0, 1, 0, 0, 0}; 前 4 维是四元数，后 3 维是平移。
            problem.AddParameterBlock(parameters, 7, new PoseSE3Parameterization());//优化初值

            addIntensityCostFactor(downsampledDisCloud,laserCloudDisMap,problem,loss_function);
            addEdgeCostFactor(downsampledEdgeCloud,laserCloudCornerMap,problem,loss_function);
            addSurfCostFactor(downsampledSurfCloud,laserCloudSurfMap,problem,loss_function);
            //配置求解器
            ceres::Solver::Options options; 
            options.linear_solver_type = ceres::DENSE_QR;
            options.max_num_iterations = 4;
            options.minimizer_progress_to_stdout = false;
            options.check_gradients = false;
            options.gradient_check_relative_precision = 1e-4;
            //求解
            ceres::Solver::Summary summary;
            ceres::Solve(options, &problem, &summary);

        }
    }else{
        printf("not enough points in map to associate, map error");
    }
    //getSceneflow(last_downsampledDisCloud,tmpcloudptr_1);
    last_downsampledDisCloud=pcl::PointCloud<pcl::PointXYZI>::Ptr(new pcl::PointCloud<pcl::PointXYZI>());
    for(int i=0;i<tmpcloudptr_1->points.size();i++)
        last_downsampledDisCloud->push_back(tmpcloudptr_1->points[i]);

    q_w_curr.normalize();
    odom.linear() = q_w_curr.toRotationMatrix();
    odom.translation() = t_w_curr;
    addPointsToMap(downsampledEdgeCloud,downsampledSurfCloud);

}

其中ceres库的主干如下

//1.构建优化问题
ceres::LossFunction *loss_function = new ceres::HuberLoss(0.1);//损失函数
//先声明一个ceres::Problem::Options,然后再用Options初始化problem
ceres::Problem::Options problem_options;
ceres::Problem problem(problem_options);
//Problem::AddParameterBlock() 添加参数模块
//表示位姿增量double parameters[7] = {0, 0, 0, 1, 0, 0, 0}; 前 4 维是四元数，后 3 维是平移。
problem.AddParameterBlock(parameters, 7, new PoseSE3Parameterization());//优化初值
//添加代价函数和损失函数
addIntensityCostFactor(downsampledDisCloud,laserCloudDisMap,problem,loss_function);
addEdgeCostFactor(downsampledEdgeCloud,laserCloudCornerMap,problem,loss_function);
addSurfCostFactor(downsampledSurfCloud,laserCloudSurfMap,problem,loss_function);
//2.配置求解器
ceres::Solver::Options options; 
options.linear_solver_type = ceres::DENSE_QR;
options.max_num_iterations = 4;
options.minimizer_progress_to_stdout = false;
options.check_gradients = false;
options.gradient_check_relative_precision = 1e-4;
//3.求解
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);

1.构建优化问题

1.1损失函数

ceres::LossFunction *loss_function = new ceres::HuberLoss(0.1);

残差大于0.1的点 ,则权重降低,具体效果看上面的公式. 小于0.1 则认为正常,不做特殊的处理

1.2创建求解的problem

ceres::Problem::Options problem_options; ceres::Problem problem(problem_options);

1.3添加参数块

表示位姿增量double parameters[7] = {0, 0, 0, 1, 0, 0, 0}; 前 4 维是四元数，后 3 维是平移。

problem.AddParameterBlock(parameters, 7, new PoseSE3Parameterization());//优化初值

优化变量PoseSE3Parameterization定义，是官方定义的LocalParameterization子类。

class PoseSE3Parameterization : public ceres::LocalParameterization {
public:
  
    PoseSE3Parameterization() {}
    virtual ~PoseSE3Parameterization() {}
    virtual bool Plus(const double* x, const double* delta, double* x_plus_delta) const;
    virtual bool ComputeJacobian(const double* x, double* jacobian) const;
    virtual int GlobalSize() const { return 7; }//参数块 x 所在的环境空间的维度。
    virtual int LocalSize() const { return 6; }// Δ 所在的切线空间的维度
};

LocalParameterization

> LocalParameterization类的作用是解决非线性优化中的过参数化问题。所谓过参数化，即待优化参数的实际自由度小于参数本身的自由度。例如在SLAM中，当采用四元数表示位姿时，由于四元数本身的约束（模长为1），实际的自由度为3而非4。此时，若直接传递四元数进行优化，冗余的维数会带来计算资源的浪费，需要使用Ceres预先定义的QuaternionParameterization对优化参数进行重构

其中的自定义的四元数加法和雅可比矩阵的计算方法如下：
- 向量到反对称矩阵转换函数skew

/* skew mat 向量到反对称矩阵的转换
 * 0 1 2    0       -mat_in(2)      mat_in(1)
 * 0 1 2    0           0           -mat_in(0);
 * 0 1 2    -mat_in(1) mat_in(0)        0
 * */
Eigen::Matrix<double,3,3> skew(Eigen::Matrix<double,3,1>& mat_in){
    Eigen::Matrix<double,3,3> skew_mat;
    skew_mat.setZero();
    skew_mat(0,1) = -mat_in(2);
    skew_mat(0,2) =  mat_in(1);
    skew_mat(1,2) = -mat_in(0);
    skew_mat(1,0) =  mat_in(2);
    skew_mat(2,0) = -mat_in(1);
    skew_mat(2,1) =  mat_in(0);
    return skew_mat;
}

• 李代数到四元数的转换

/**
 * @brief 根据李代数SE(3)计算位姿的四元数和平移向量
 *
 * @param se3 6维李代数SE(3)类型，表示位姿的旋转部分和平移部分的组合
 * @param q 四元数对象，计算得到的位姿的旋转部分
 * @param t 平移向量对象，计算得到的位姿的平移部分
 */
void getTransformFromSe3(const Eigen::Matrix<double,6,1>& se3, Eigen::Quaterniond& q, Eigen::Vector3d& t){
    // 将6维李代数SE(3)中的旋转部分和平移部分分别赋值给对应的Eigen库中的向量对象
    Eigen::Vector3d omega(se3.data()); // 旋转
    Eigen::Vector3d upsilon(se3.data()+3); // 平移
    // 计算旋转部分向量的反对称矩阵Omega
    Eigen::Matrix3d Omega = skew(omega);
    // 计算旋转部分向量的2范数
    double theta = omega.norm();
    double half_theta = 0.5*theta;
    double imag_factor;
    double real_factor = cos(half_theta);
    // 计算四元数的虚部系数imag_factor
    if(theta<1e-10)
    {
        double theta_sq = theta*theta;
        double theta_po4 = theta_sq*theta_sq;
        imag_factor = 0.5-0.0208333*theta_sq+0.000260417*theta_po4;
    }
    else
    {
        double sin_half_theta = sin(half_theta);
        imag_factor = sin_half_theta/theta;
    }
    // 根据实部系数real_factor和虚部系数imag_factor，以及旋转部分向量omega计算四元数q
    q = Eigen::Quaterniond(real_factor, imag_factor*omega.x(), imag_factor*omega.y(), imag_factor*omega.z());
    Eigen::Matrix3d J;
    // 计算变换矩阵J和平移向量t
    if (theta<1e-10)
    {
        J = q.matrix();
    }
    else
    {
        Eigen::Matrix3d Omega2 = Omega*Omega;
        J = (Eigen::Matrix3d::Identity() + (1-cos(theta))/(theta*theta)*Omega + (theta-sin(theta))/(pow(theta,3))*Omega2);
    }
    t = J*upsilon; // 平移向量t由变换矩阵J和平移部分向量upsilon相乘得到
}

• 自定义的李代数加法

/**
 * @brief 实现李代数SE(3)的加法运算
 *
 * @param x 李代数SE(3)类型，表示位姿的旋转部分和平移部分的组合
 * @param delta 变化量，可以看作李代数SE(3)中的扰动量
 * @param x_plus_delta 李代数SE(3)类型，表示相加得到的新的位姿
 * @return bool 返回值始终为true
 */
bool PoseSE3Parameterization::Plus(const double *x, const double *delta, double *x_plus_delta) const {
    // 指定一个double数组的连续内存区域，并将其解释为Eigen库中的向量类型
    Eigen::Map<const Eigen::Vector3d> trans(x + 4);
    // 定义四元数对象和平移向量对象
    Eigen::Quaterniond delta_q;
    Eigen::Vector3d delta_t;
    // 将6维李代数变换(delta)分别转换成四元数和平移向量进行描述
    getTransformFromSe3(Eigen::Map<const Eigen::Matrix<double,6,1>>(delta), delta_q, delta_t);
    // 指定一个double数组的连续内存区域，并将其解释为Eigen库中的常量四元数类型
    Eigen::Map<const Eigen::Quaterniond> quater(x);
    // 指定一个double数组的连续内存区域，并将其解释为Eigen库中的四元数类型
    Eigen::Map<Eigen::Quaterniond> quater_plus(x_plus_delta);
    // 指定一个double数组的连续内存区域，并将其解释为Eigen库中的向量类型
    Eigen::Map<Eigen::Vector3d> trans_plus(x_plus_delta + 4);
    // 新位姿的旋转部分由delta_q和原始位姿的旋转部分相乘得到
    quater_plus = delta_q * quater;
    // 新位姿的平移部分由delta_q和原始位姿的平移部分相乘并加上delta_t得到
    trans_plus = delta_q * trans + delta_t;

    return true;
}

• 自定义的雅可比矩阵计算

// PoseSE3Parameterization 类的 ComputeJacobian 函数实现
// 该函数用于计算长度为 7 的一维数组 x 对应的 6*7 Jacobian 矩阵，并将结果存储在 jacobian 指向的内存区域中
// 参数说明：
// x：长度为 7 的一维 double 数组
// jacobian：指向长度为 42（6*7）的 double 数组的指针
bool PoseSE3Parameterization::ComputeJacobian(const double *x, double *jacobian) const {
    // 使用 Eigen 中的 Map 函数将 jacobian 数组映射到 Eigen Matrix 类型的对象 j 上，并指定其行优先存储方式。
    Eigen::Map<Eigen::Matrix<double, 7, 6, Eigen::RowMajor>> j(jacobian);
    // 设置 j 的前六行为单位矩阵，即对于每个旋转和平移参数，其导数为1。
    (j.topRows(6)).setIdentity();
    // 设置 j 的最后一行为零，因为位姿不受时间变量影响。
    (j.bottomRows(1)).setZero();
    // 返回 true 表示计算成功完成。
    return true;
}

1.4 添加代价函数

addIntensityCostFactor添加强度残差计算

addIntensityCostFactor(downsampledDisCloud,laserCloudDisMap,problem,loss_function);

函数内部：

void OdomEstimationClass::addIntensityCostFactor(const pcl::PointCloud<pcl::PointXYZI>::Ptr& pc_in, const pcl::PointCloud<pcl::PointXYZI>::Ptr& map_in, ceres::Problem& problem, ceres::LossFunction *loss_function){
    int dis_num=0;
    for (int i = 0; i < (int)pc_in->points.size(); i++)
    {

        // if(pc_in->points[i].intensity<0.1)
        //     continue;
        pcl::PointXYZI point_temp;
        //将点从当前坐标转化为地图中的坐标
        pointAssociateToMap(&(pc_in->points[i]), &point_temp);
        std::vector<int> pointSearchInd;
        std::vector<float> pointSearchSqDis;
        //kdtreeEdgeMap->nearestKSearch(point_temp, 5, pointSearchInd, pointSearchSqDis); 
        if(kdtreeDisMap->radiusSearch(point_temp, 1.5, pointSearchInd, pointSearchSqDis)<3)//7
            continue;
        else if(pointSearchSqDis[0]<1.0){//最近距离小于1
            
            float intensity_derivative[8]={0,0,0,0,0,0,0,0};
            //根据强度信息计算导数，差分近似，将目标点半径1.5m内的点的平均强度减去当前点的强度作为导数
            calculateDerivative(map_in->points[i],pointSearchInd,map_in,intensity_derivative);
            Eigen::Vector3d curr_point(pc_in->points[i].x, pc_in->points[i].y, pc_in->points[i].z);
            Eigen::Vector3d nearest_point(map_in->points[pointSearchInd[0]].x,map_in->points[pointSearchInd[0]].y,map_in->points[pointSearchInd[0]].z);
            //代价函数创建，构造函数为传入导数值
            ceres::CostFunction *cost_function = new IntensityAnalyticCostFunction(curr_point, nearest_point, pc_in->points[i].intensity - map_in->points[pointSearchInd[0]].intensity, intensity_derivative, 1.0);  
            problem.AddResidualBlock(cost_function, loss_function, parameters);
            dis_num++;
        }
    }
    if(dis_num<10){
        printf("not enough correct points");
    }
}

IntensityAnalyticCostFunction定义

• 定义：

class IntensityAnalyticCostFunction : public ceres::SizedCostFunction<1, 7> {
  public:
IntensityAnalyticCostFunction(Eigen::Vector3d curr_point_, Eigen::Vector3d nearest_point_, float intensity_residual_, float intensity_derivative_[],  float weight);
virtual ~IntensityAnalyticCostFunction() {}
virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;
Eigen::Vector3d curr_point;
Eigen::Vector3d nearest_point;
double intensity_residual;
double intensity_derivative[8];
double weight;
};

• Evaluate函数

  这个函数计算给定参数的强度分析代价函数
  输入参数包括相机当前姿态的四元数和平移向量
  函数将当前点从相机坐标系转换到世界坐标系
  代价函数由当前点的强度与地图上最近点的强度之间的差异构成
  函数同时计算雅可比矩阵，用于在捆绑调整BA过程中优化参数

/**
@brief 对当前点的强度与最近邻点的强度之差进行成本函数的评估
@param parameters 一个二重指针，包含当前帧的四元数和平移向量信息
@param residuals 存储残差的数组，计算成本函数得到的值
@param jacobians 存储雅可比矩阵的二重指针，用于优化求解
@return bool 始终返回true
*/
bool IntensityAnalyticCostFunction::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
// 将四元数和平移向量从输入参数中映射到Eigen向量中
    Eigen::Map<const Eigen::Quaterniond> q_w_curr(parameters[0]);
    Eigen::Map<const Eigen::Vector3d> t_w_curr(parameters[0] + 4);
    // 将当前点从当前坐标系转换到世界坐标系
    Eigen::Vector3d point_w = q_w_curr * curr_point + t_w_curr;
    //f(xi) = I(p)- I(p')
    //I(p) = xyz_radius * delta_intensity
    // 计算当前点与地图上最近点之间的距离
    double delta_x = point_w.x()-nearest_point.x();
    double delta_y = point_w.y()-nearest_point.y();
    double delta_z = point_w.z()-nearest_point.z();
    double xy_radius_square = std::max(delta_x*delta_x+delta_y*delta_y,0.0000004);
    double xy_radius = std::sqrt(xy_radius_square);
    double xyz_radius_square = std::max(xy_radius_square + delta_z*delta_z,0.0000004);
    double xyz_radius = std::sqrt(xyz_radius_square);
    double theta_1 = std::atan2(delta_z,xy_radius);
    double theta_2 = std::atan2(delta_y,delta_x);
    
// 初始化四元数和旋转角度
    double q1 = 0.0;
    double q2 = 0.0;
    double q3 = 0.0;
    double q4 = 0.0;
    double angle_shifts = 0.0;
    /**
    如果 theta_2 的值大于等于 -0.75M_PI 并且小于 -0.25M_PI，则对变量 q1、q2、q3 和 q4 分别进行计算并赋值，最后将 angle_shifts 赋为 0.5*M_PI。

在下一个 else if 语句中，如果 theta_2 的值大于等于 -0.25M_PI 并且小于 0.25M_PI，则对变量 q1、q2、q3 和 q4 分别进行计算并赋值，最后将 angle_shifts 赋为 0.0。

在下一个 else if 语句中，如果 theta_2 的值大于等于 0.25M_PI 并且小于 0.75M_PI，则对变量 q1、q2、q3 和 q4 分别进行计算并赋值，最后将 angle_shifts 赋为 -0.5*M_PI。

在最后的 else 语句中，如果 theta_2 的值不属于上述范围，则对变量 q1、q2、q3 和 q4 分别进行计算并赋值，最后将 angle_shifts 赋为 0.0。
    */
    if(theta_2>=-0.75*M_PI &&theta_2<-0.25*M_PI){
        q1 = (intensity_derivative[2]+intensity_derivative[6])/2;
        q2 = (intensity_derivative[2]-intensity_derivative[6])/2;
        q3 = (intensity_derivative[3]+intensity_derivative[7])/2;
        q4 = (intensity_derivative[3]-intensity_derivative[7])/2;
        angle_shifts = 0.5*M_PI;
    }else if(theta_2>=-0.25*M_PI &&theta_2<0.25*M_PI){
        q1 = (intensity_derivative[0]+intensity_derivative[2])/2;
        q2 = (intensity_derivative[0]-intensity_derivative[2])/2;
        q3 = (intensity_derivative[1]+intensity_derivative[3])/2;
        q4 = (intensity_derivative[1]-intensity_derivative[3])/2;
        angle_shifts = 0.0;
    }else if(theta_2>=0.25*M_PI &&theta_2<0.75*M_PI){
        // p1 = (intensity_derivative[4]+intensity_derivative[0])/2 +  (intensity_derivative[4]-intensity_derivative[0])/2 *(sin(2*(theta_2-0.5*M_PI)));
        // p2 = (intensity_derivative[5]+intensity_derivative[1])/2 +  (intensity_derivative[5]-intensity_derivative[1])/2 *(sin(2*(theta_2-0.5*M_PI)));
        q1 = (intensity_derivative[4]+intensity_derivative[0])/2;
        q2 = (intensity_derivative[4]-intensity_derivative[0])/2;
        q3 = (intensity_derivative[5]+intensity_derivative[1])/2;
        q4 = (intensity_derivative[5]-intensity_derivative[1])/2;
        angle_shifts = -0.5*M_PI;
    }else{
        // p1 = (intensity_derivative[6]+intensity_derivative[4])/2 +  (intensity_derivative[6]-intensity_derivative[4])/2 *(sin(2*(theta_2)));
        // p2 = (intensity_derivative[7]+intensity_derivative[5])/2 +  (intensity_derivative[7]-intensity_derivative[5])/2 *(sin(2*(theta_2)));
        q1 = (intensity_derivative[6]+intensity_derivative[4])/2;
        q2 = (intensity_derivative[6]-intensity_derivative[4])/2;
        q3 = (intensity_derivative[7]+intensity_derivative[5])/2;
        q4 = (intensity_derivative[7]-intensity_derivative[5])/2;
        angle_shifts = 0.0;
    }

    double p1 = q1 + q2 *(sin(2*(theta_2 + angle_shifts)));
    double p2 = q3 + q4 *(sin(2*(theta_2 + angle_shifts)));
    double delta_intensity = (p1+p2)/2 + (p1-p2)/2 * sin(2*theta_1);
    residuals[0] = weight * (delta_intensity - intensity_residual);
    //residuals[0] = xyz_radius;
    //residuals[0] = xyz_radius * delta_intensity;
    Eigen::Matrix<double, 1, 2> dintensity_by_dtheta;
    dintensity_by_dtheta(0,0) = (p1 - p2) * cos(2*theta_1);
    dintensity_by_dtheta(0,1) = (q2 + q4 + (q2 - q4) * sin(2*theta_1)) * cos(2*(theta_2 + angle_shifts));

    Eigen::Matrix<double, 2, 3> dtheta_by_dp;
    dtheta_by_dp(0,0) = -delta_x*delta_z/(xy_radius*xyz_radius_square);
    dtheta_by_dp(0,1) = -delta_y*delta_z/(xy_radius*xyz_radius_square);
    dtheta_by_dp(0,2) = xy_radius/(xyz_radius_square);

    dtheta_by_dp(1,0) = -delta_y/xy_radius_square;
    dtheta_by_dp(1,1) = delta_x/xy_radius_square;
    dtheta_by_dp(1,2) = 0.0;

    Eigen::Matrix<double, 1, 3> dradius_by_dp;
    dradius_by_dp(0,0) = delta_x/xyz_radius;
    dradius_by_dp(0,1) = delta_y/xyz_radius;
    dradius_by_dp(0,2) = delta_z/xyz_radius;

    Eigen::Vector3d test_vector(delta_x/xyz_radius,delta_y/xyz_radius,delta_z/xyz_radius);
    if(jacobians != NULL)
    {
        if(jacobians[0] != NULL)
        {
            Eigen::Matrix3d skew_point_w = skew(point_w);

            Eigen::Matrix<double, 3, 6> dp_by_so3;
            dp_by_so3.block<3,3>(0,0) = -skew_point_w;
            (dp_by_so3.block<3,3>(0, 3)).setIdentity();
            Eigen::Map<Eigen::Matrix<double, 1, 7, Eigen::RowMajor>> J_se3(jacobians[0]);
            J_se3.setZero();
            //[f(x,y,z)g(x,y,z)]' = f'(x,y,z)g(x,y,z)+f(x,y,z)g'(x,y,z)
            // J_se3.block<1,6>(0,0) =  dradius_by_dp * dp_by_so3;
            J_se3.block<1,6>(0,0) =  weight * (/*dradius_by_dp * delta_intensity + */xyz_radius * dintensity_by_dtheta * dtheta_by_dp) * dp_by_so3;  //不加radius 效果好一点？？？？
        }
    }
    return true;
} 

强度导数计算

void OdomEstimationClass::calculateDerivative(pcl::PointXYZI& point_in, std::vector<int>& pointSearchInd, const pcl::PointCloud<pcl::PointXYZI>::Ptr& map_in, float intensity_derivative[]){

    //calculate average 
    //calculate derivative
    ///0 x,y,z>=0
    ///1 x>0,y>0,z<0
    ///2 x>0,y<0,z>0
    ///3 x>0,y<0,z<0
    ///4 x<0,y>0,z>0
    ///5 x<0,y>0.z<0
    ///6 x<0,y<0,z>0
    ///7 x<0,y<0,z<0
    int intensity_count[8]={0,0,0,0,0,0,0,0};
    //根据点的坐标判断方向，类似于八叉树
    for(int i=1;i<(int)pointSearchInd.size();i++){
        int position_id = 0;
        //第i个点离最近点的x方向距离小于0 position_id+4
        if(map_in->points[pointSearchInd[i]].x - map_in->points[pointSearchInd[0]].x >= 0){
            position_id+=0;
        }else{
            position_id+=4;
        }
        //第i个点离最近点的y方向距离小于0 position_id+2
        if(map_in->points[pointSearchInd[i]].y - map_in->points[pointSearchInd[0]].y >= 0){
            position_id+=0;
        }else{
            position_id+=2;
        }
        //第i个点离最近点的z方向距离小于0 position_id+1
        if(map_in->points[pointSearchInd[i]].z - map_in->points[pointSearchInd[0]].z >= 0){
            position_id+=0;
        }else{
            position_id+=1;
        }

        intensity_count[position_id] += 1;
        intensity_derivative[position_id]+= map_in->points[pointSearchInd[i]].intensity;
    }
    //assign to derivative
    for(int i=0;i<8;i++){
        if(intensity_count[i]!=0)
            intensity_derivative[i] = intensity_derivative[i]/intensity_count[i] - map_in->points[pointSearchInd[0]].intensity;
        else
            intensity_derivative[i] = -1;// - map_in->points[pointSearchInd[0]].intensity; 
    }
}

addEdgeCostFactor 为边角点添加残差块
addSurfCostFactor 为表面点添加残差块

addEdgeCostFactor(downsampledEdgeCloud,laserCloudCornerMap,problem,loss_function); addSurfCostFactor(downsampledSurfCloud,laserCloudSurfMap,problem,loss_function);