Leetcode-每日一题【剑指 Offer 07. 重建二叉树】

题目

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

• 0 <= 节点个数 <= 5000

解题思路

1.题目要求我们利用前序遍历和中序遍历构建出二叉树，我们可以画图来理解一下

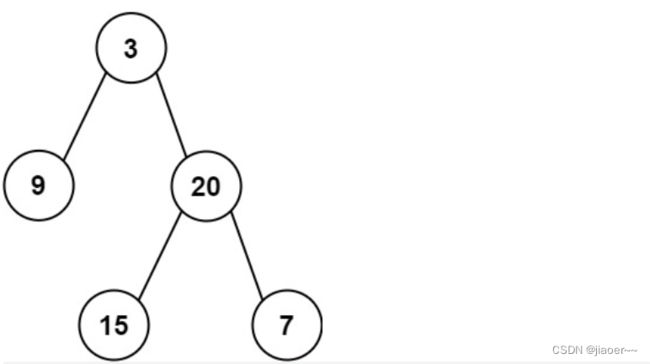
举个例子：

根据我们对数据结构中二叉树部分的学习，我们知道前序遍历是（根左右）所以第一个元素一定是这颗二叉树的根。

 

那么中序遍历是（左右根），所以数字 3 左边的是它的左子树部分，右边的是他的右子树部分。 设 3 在数组 inorder中的下标为 i，

前序遍历：左子树部分 [ l1 + 1, l1 + (i - l2) ]     右子树部分 [l2, i - 1]

中序遍历：左子树部分 [l1 + (i - l2) + 1, r1]    右子树部分[i + 1, r2]

 

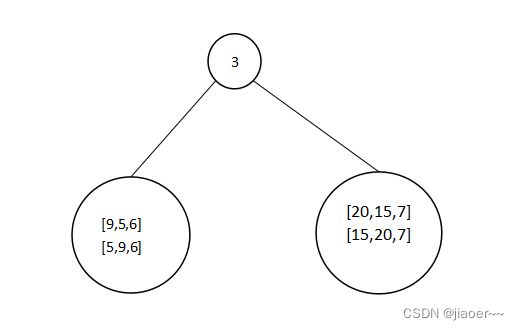
 我们按照这个思想继续处理 3 的左子树和右子树， 也就是进行递归操作，

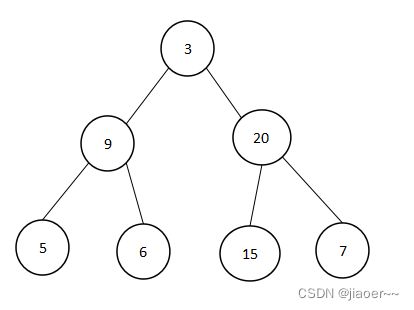
3 的左子树中 9 为根节点，那么 5 和 6 为 9 的左右子树，3 的右子树中 20 为根节点，15 和7 为 3 的左右子树。最终生成的数如下图所示

 2.代码部分首先我们判断所给数组是否为空，若为空直接返回 null；然后我们新建一个map 用于存储inorder数组的下标和对应的值，方便我们后序对 root 所对应的数组下标进行查找。

然后我们让root = f( ) 函数。

3.f( ) 函数的作用是利用传入的前序遍历和中序遍历的数组，找到二叉树的 root 节点，并将数组划分为 root 节点的左右子树。结束条件为 r1 < l1 && r2 < l2。处理完成后返回 root 即可。

代码实现

class Solution {
     Map map = new HashMap();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || preorder.length <= 0){
            return null;
        }
        for(int i = 0; i < inorder.length; i++){
            map.put(inorder[i],i);
    }
    TreeNode root = f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
         return root;
    }
    public TreeNode f(int[] preorder, int l1, int r1, int[] inorder, int l2, int r2){
        if(r1 < l1 && r2 < l2){
            return null;
        }
        TreeNode root = new TreeNode(preorder[l1]);
        int i = map.get(preorder[l1]);
        root.left = f(preorder, l1 + 1, l1 + (i - l2), inorder, l2, i - 1);
        root.right = f(preorder,l1 + (i - l2) + 1, r1, inorder, i + 1, r2);
        return root;

    }
}

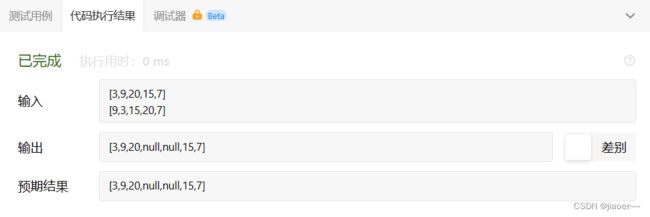
测试结果