(C语言)浅析求最大公约数的四种算法

求最大公约数最常见的算法有枚举法和辗转相除法，在这里梳理一下求最大公约数的四种算法。

求最大公约数的四种算法分别是：

1.辗转求余法

 2.穷举法

 3.更相减损法

 4."Stein"算法

1.辗转求余法

算法描述

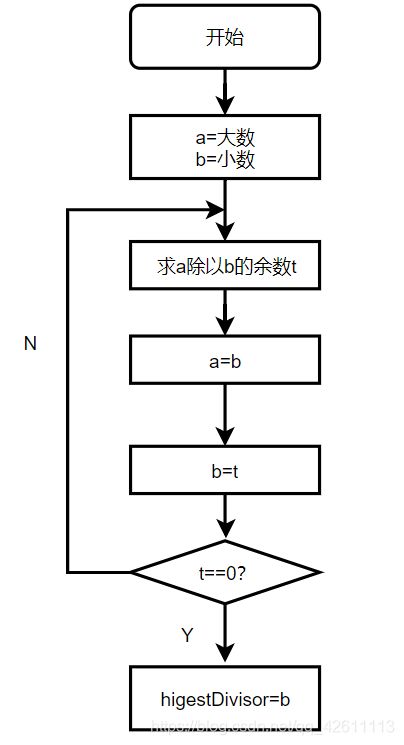
用大数除以小数得到余数，然后用前一步的除数除以前一步的余数，相除得到新余数，如此往复，直到余数为0为止，此时的除数就是最大公约数。

eg：求125和45的最大公约数

125%45=35

45%35=10

35%10=5

10%5=0

最大公约数：5

伪代码描述

①嵌套调用

a=大数;

b=小数;

while(t不为0)

{

   t=a%b;

   a=b;

   b=t;

}

②递归调用

gcd ( a,b)

{  

if( a % b不为0)

        return b;   

else  

        return gcd(b,a%b);

  }

辗转相除法流程图

             

代码实现           

//辗转相除法1-函数嵌套调用
int GCD1(int a,int b)
{
	int t=0;
	if( a < b)//交换a,b,保证大数放在a中，小数放在b中
	{
		t=a;
		a=b;
		b=t;
	}
	while(b)//辗转相除  若b(除数)不为0
	{
		t=a % b;//求a/b的余数
		a=b; 
		b=t;
	}
	return a;//返回求得的最大公约数
}

 

//辗转相除法2-函数递归调用
int GCD2(int a,int b)
{
	return !(a%b)? b : GCD2(b,a%b); 
}

2.穷举法

算法描述

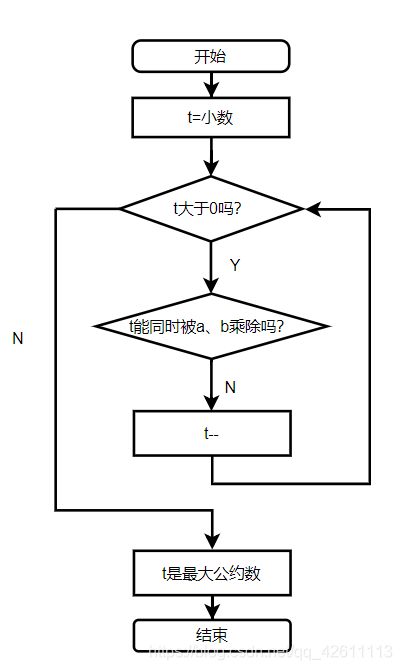
从两数中的较小数开始，由大到小列举，直到找到最大公约数为止，中断列举，得到的公约数便是最大公约数。

eg：求12和的最大公约数

从8开始列举：

8能同时被12,8整除吗？ N

7能同时被12,8整除吗？ N

6能同时被12,8整除吗？ N

5能同时被12,8整除吗？ N

4能同时被12,8整除吗？ Y！

最大公约数：4

伪代码描述

t=小数;

while(t>0)

{

   if(t同时被a和b整除)

       break;

   else

       t--;

}

穷举法流程图

代码实现

//穷举法
int GCD3(int a,int b)
{
	int t=(a>b)? b:a;//把两个数的较小值赋给t
	while(t>0)
	{
		if(a%t==0&&b%t==0)
		{
			break;//只要找到一个数能同时被a，b整除，就终止循环
		}
		t--;
	}
	return t;
}

3.更相减损法

算法描述：

I 任意给定两个正整数，判断它们是否都是偶数。若是，则用2约简；若不是则执行II。

II 用较大数减较小数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。
则I中约掉的若干个2与II中等数的乘积就是所求的最大公约数，得到的“等数”就是最大公约数。

eg:求24和6的最大公约数

24和6能同时被2整除整除吗？ Y   用2约简

12和3能同时被2整除吗？   N  转到第二步

12-3=9

9-3=6

6-3=3           3=3

最大公约数：2*3=6

伪代码描述：

while(a和b能同时被2整除)

{

    用2约简a,b

    t++;

}

 while(a != b)

{

   更相减损;

}

return 2*t*a;

更相减损法流程图：

 

代码实现

//更相减损法
int GCD4(int a,int b)
{
	int  t=0;
	while(a%2==0 && b%2==0)//判断a和b能被多少个2整除 
	{
		a/=2;
		b/=2; 
		t++;
	}

	 while(a != b) //更相减损 
	{
		(a>b)? a-=b : b-=a ;
	}
	return t==0? a : 2*t*a;
} 

4."Stein"算法

算法描述：

计算一个偶数和一个奇数的最大公约数时，可以先将偶数除以2。

设置A1 = A、B1=B和C1 = 1

如果An=Bn，An(Bn)是最大公约数，算法结束

1.如果An和Bn都是偶数，则A(n+1) =An /2，B(n+1) =Bn /2，C(n+1) =Cn *2(乘2把整数左移一位即可，除2把整数右移一位) ,fac++

2.如果An是偶数，Bn是奇数，则A(n+1) =An /2，B(n+1) =Bn ，C(n+1) =Cn

3.如果An是奇数，Bn是偶数，则B(n+1) =Bn /2，An+1 =An ，C(n+1) =Cn

4.如果An和Bn都是奇数，则A(n+1) =|An -Bn|，B(n+1) =min(An,Bn)，C(n+1) =Cn

5.转1

6. a<

eg:求84和7的最大公约数

A1=84  B1=7  C1=1

84是偶数 7是奇数  A2=A1/2=84/2=42       B2=B1=7          C2=C1=1   

42是偶数 7是奇数  A3=A2/2=41/2=21       B3=B2=7          C3=C2=1

21是奇数 7是奇数  A4=|A3-B3|=21-7=14     B4=min(A3,B3)=7  C4=C3=1

14是偶数 7是奇数  A5=A4/2=14/2=7        B5=B4=7          C5=C4=1

A5=B5=7           

最大公约数:7

伪代码描述：

while(a和b不相等）

{

   if(a是偶数)

       b是偶数？  a，b右移一位 ： （a右移一位，fac++）

   if(a是奇数)

       b是奇数？ (a=|a-b|,b=min(a,b);) : b右移一位

}

最大公约数=a<

流程图描述

代码实现

//Stein算法1-非递归 
int GCD5(int a,int b)
{
	int factor = 0,t;
	if(a>1;
				a-=b;
			}
			else//当a是奇数b是偶数时 
			{
				b>>=1;
			}
		}
		else //当a是偶数时 
		{
			if(b%2)//当a是偶数b是奇数时 
			{
				a>>=1;
				 if(a < b)
				 {
				 	t=a;
				 	a=b;
				 	b=t;
				 }
			}
			else//当a和b都是偶数时 
			{
				a>>=1;
				b>>=1;
				++factor;
			}
		
		}
	}
	return a<

//Stein算法1-非递归 
int GCD5(int a,int b)
{
	int factor = 0,t;
	if(a>1;
				a-=b;
			}
			else//当a是奇数b是偶数时 
			{
				b>>=1;
			}
		}
		else //当a是偶数时 
		{
			if(b%2)//当a是偶数b是奇数时 
			{
				a>>=1;
				 if(a < b)
				 {
				 	t=a;
				 	a=b;
				 	b=t;
				 }
			}
			else//当a和b都是偶数时 
			{
				a>>=1;
				b>>=1;
				++factor;
			}
		
		}
	}
	return a<

最后一种算法本人还没有太理解，所以可能代码本身还存在一定的问题，仅供参考......

附：程序源代码

#include
#include
#include
#include
using namespace std;

//辗转相除法1-函数嵌套调用
int GCD1(int a,int b)
{
	int t=0;
	if( a < b)//交换a,b,保证大数放在a中，小数放在b中
	{
		t=a;
		a=b;
		b=t;
	}
	while(b)//辗转相除  若b(除数)不为0
	{
		t=a % b;//求a/b的余数
		a=b; 
		b=t;
	}
	return a;//返回求得的最大公约数
}

//辗转相除法2-函数递归调用
int GCD2(int a,int b)
{
	return !(a%b)? b : GCD2(b,a%b); 
}

//穷举法
int GCD3(int a,int b)
{
	int t=(a>b)? b:a;//把两个数的较小值赋给t
	while(t>0)
	{
		if(a%t==0&&b%t==0)
		{
			break;//只要找到一个数能同时被a，b整除，就终止循环
		}
		t--;
	}
	return t;
}

//更相减损法
int GCD4(int a,int b)
{
	int  t=0;
	while(a%2==0 && b%2==0)//判断a和b能被多少个2整除 
	{
		a/=2;
		b/=2; 
		t++;
	}

	 while(a != b) //更相减损 
	{
		(a>b)? a-=b : b-=a ;
	}
	return t==0? a : 2*t*a;
} 

//Stein算法1-非递归 
int GCD5(int a,int b)
{
	int factor = 0,t;
	if(a>1;
				a-=b;
			}
			else//当a是奇数b是偶数时 
			{
				b>>=1;
			}
		}
		else //当a是偶数时 
		{
			if(b%2)//当a是偶数b是奇数时 
			{
				a>>=1;
				 if(a < b)
				 {
				 	t=a;
				 	a=b;
				 	b=t;
				 }
			}
			else//当a和b都是偶数时 
			{
				a>>=1;
				b>>=1;
				++factor;
			}
		
		}
	}
	return a<