K最近邻算法：简单高效的分类和回归方法

简介

K最近邻（K-nearest neighbors，简称KNN）算法是一种基于实例的机器学习方法，可以用于分类和回归问题。它的思想非常简单，但在实践中却表现出了出色的效果。本文将介绍KNN算法的原理、应用场景和优缺点，并通过示例代码演示其实现过程

---

KNN算法原理

KNN算法基于一个假设：相似的样本具有相似的特征。它的工作流程如下

• 计算待分类样本与训练集中每个样本之间的距离（通常使用欧氏距离或曼哈顿距离）
• 选取距离最近的K个样本作为邻居
• 根据邻居样本的标签进行投票，将待分类样本归类为得票最多的类别（分类问题）或计算邻居样本标签的平均值（回归问题）
  欧拉距离如下
  

---

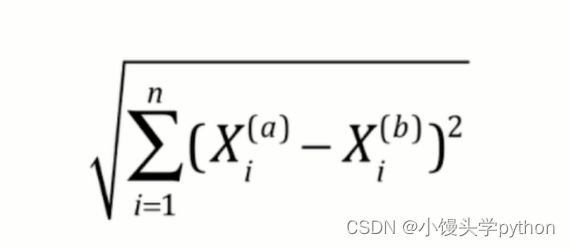
KNN算法应用场景

KNN算法在以下场景中广泛应用

• 分类问题：如垃圾邮件过滤、图像识别等
• 回归问题：如房价预测、股票价格预测等
• 推荐系统：根据用户和物品的相似度进行推荐
• 异常检测：检测异常行为或异常事件

例如在邮件分类上就需要如下步骤

• 数据准备：
  为了使用KNN算法进行邮件分类，我们需要准备一个数据集作为训练样本。这个数据集可以由已标记为垃圾邮件和非垃圾邮件的邮件组成。每封邮件都应该被转化为特征向量表示，通常使用词袋模型来表示每个邮件中的单词频率。

• 特征提取：
  对于每封邮件，我们可以提取出一组特征，例如：

• 单词频率：统计邮件中每个单词的出现频率，构建一个向量表示邮件的特征。
  主题关键词：根据主题模型提取关键词，构建一个向量表示邮件的主题内容。

• 数据预处理：
  在应用KNN算法之前，需要对数据进行预处理。常见的预处理步骤包括去除停用词、词干提取和编码转换等。

• 模型训练：
  将预处理后的数据集划分为训练集和测试集。使用KNN算法对训练集进行训练，调整K值和距离度量方式来优化模型性能。可以通过交叉验证等技术来选择最优的K值。

• 模型评估：
  使用训练好的模型对测试集进行预测，并与真实标签进行比较。常用的评估指标包括准确率、精确率、召回率和F1值等，通过这些指标可以评估模型在垃圾邮件过滤方面的性能。

• 模型使用：
  将训练好的模型应用于新的邮件数据分类。通过计算待分类邮件与训练集样本的距离，并选取最近的K个邻居样本，根据这些邻居样本的标签进行投票，将待分类邮件划分为得票最多的类别，即确定该邮件是否为垃圾邮件。

---

KNN算法优缺点

KNN算法有以下优点

• 简单直观，易于实现和理解
• 适用于多分类问题
• 对于样本分布不规则的情况，表现良好

然而，KNN算法也存在一些缺点

• 需要存储全部训练样本，计算复杂度较高
• 对于高维数据，效果不佳
• 对于样本不平衡的数据集，容易被少数类别影响

KNN算法代码示例

首先需要导入numpy和matplotlib这两个库

import numpy as np
from matplotlib import pyplot as plt

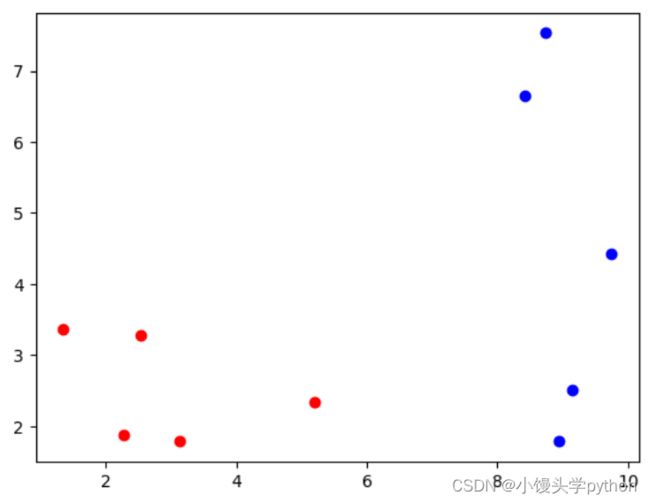
接下来将我们准备好的一组数据描绘成散点图

raw_data_X = [[5.1935, 2.3312],
              [3.1201, 1.7815],
              [1.3438, 3.3684],
              [2.5323, 3.2762],
              [2.2804, 1.8670],
              [8.4234, 6.6565],
              [8.7451, 7.5340],
              [9.1522, 2.5141],
              [9.7428, 4.4241],
              [8.9398, 1.7916]]
raw_data_y =[0, 0, 0, 0, 0, 1, 1, 1, 1, 1]  #  0是良性，1是恶性
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='r')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='b')
plt.show()

运行结果如下

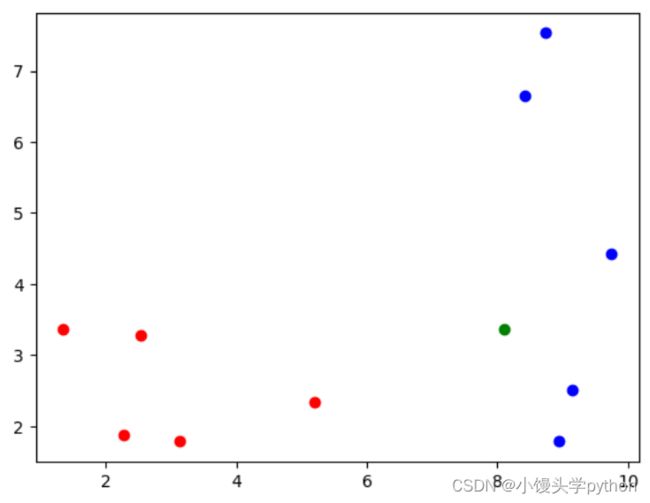
接下来，我们需要给定待预测数据，来预测它的结果，首先我们将两个待遇测数据用绿点在图中展示

x = np.array([8.0936, 3.3657])
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='r')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='b')
plt.scatter(x[0],x[1],color='g')
plt.show()

运行结果如下

根据KNN算法的原理，我们需要计算距离，所以这里我们需要导入math库
同时根据列表生成式计算distance

from math import sqrt
distance = []  # 保存和其他所有点的距离    
distance = [sqrt(np.sum((x_train-x)**2)) for x_train in X_train]

之后需要找出距离待预测点最近的k个点

k = 3
nearest = np.argsort(distance)
nearest[:k]

运行结果如下

之后将下标取出

nearest = [i for i in nearest[:k]]

运行结果如下

找出最近的k个点下标值以后，找出这些样本对应的目标值

top_K = [i for i in y_train[nearest]]

运行结果如下

下面我们需要导入一个库用来进行投票，显然0有0票，1有3票

from collections import Counter
votes = Counter(top_K)

运行结果如下

之后将预测结果输出即可

y_predict = votes.most_common(1)[0][0]

运行结果如下

总结

以上代码仅仅的简单演示一遍KNN算法，但是真正的KNN算法并没有这么简单，下节我会通过上述代码的基础上进行简单的优化，并进行封装

挑战与创造都是很痛苦的，但是很充实。