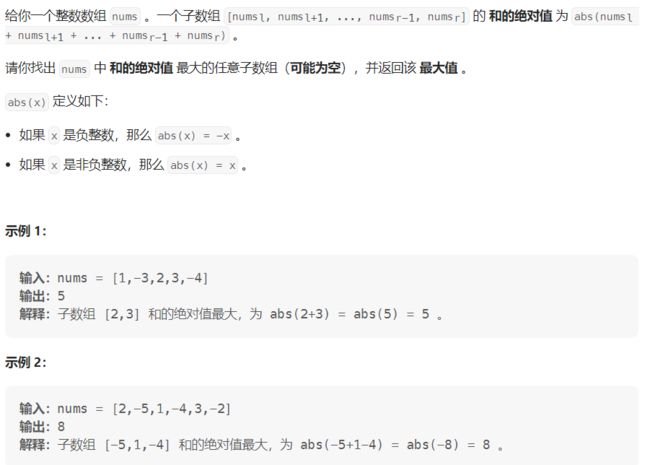
1749. 任意子数组和的绝对值的最大值

诸神缄默不语-个人CSDN博文目录
力扣刷题笔记

1. 暴力搜索

直接用2个指针从索引0开始找到最后一个索引，时间复杂度大概是$O(n^2)$吧，总之这么搞不行，以下是我用Python写的一些典型失败案例

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        max_abs=0
        nums_len=len(nums)
        for pointer1 in range(nums_len):
            for pointer2 in range(pointer1,nums_len):
                sub_nums=nums[pointer1:pointer2+1]
                max_abs=max(max_abs,abs(sum(sub_nums)))
        return max_abs

↑会超时，这个我觉得应该是sum()的问题，所以做了改进：

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        sum_table=[[0 for _ in range(len(nums))] for _ in range(len(nums))]
        for i in range(len(nums)):
            sum_table[i][i]=nums[i]
        for i in range(len(nums)):
            for j in range(i+1,len(nums)):
                sum_table[i][j]=sum_table[i][j-1]+nums[j]
        max_abs=0
        for i in sum_table:
            for j in i:
                max_abs=max(max_abs,abs(j))
        return max_abs

↑这个又会爆内存，我骂骂咧咧。
这个我一开始猜是因为0太多了，所以把所有一直都是0的部分给删除了：

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        sum_table=[[0 for _ in range(len(nums)-i)] for i in range(len(nums))]
        for i in range(len(nums)):
            sum_table[i][0]=nums[i]
        for i in range(len(nums)):
            for j in range(1,len(nums)-i):
                sum_table[i][j]=sum_table[i][j-1]+nums[j+i]
        max_abs=0
        for i in sum_table:
            for j in i:
                max_abs=max(max_abs,abs(j))
        return max_abs

↑还是会爆内存
继续缩：

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        max_abs=0
        for i in range(len(nums)):
            pre_sum=nums[i]
            max_abs=max(max_abs,abs(pre_sum))
            for j in range(i+1,len(nums)):
                pre_sum=pre_sum+nums[j]
                max_abs=max(max_abs,abs(pre_sum))
        return max_abs

这回超时了

2. 动态规划

然后我就去看题解了。

来自官方题解：https://leetcode.cn/problems/maximum-absolute-sum-of-any-subarray/solutions/2372374/ren-yi-zi-shu-zu-he-de-jue-dui-zhi-de-zu-qerr/

在一组数字中绝对值的最大值，可能是最大的值的绝对值，也可能是最小值的绝对值。
所以找子数组和绝对值的最大值，就要找最大的子数组和，和最小的子数组和。
所以解决方案是分别计算这两种情况：在找最大的子数组和时，遍历数组，保留到上一个数字为止的全局子数组最大和global_max+有上一个数字在的子数组的最大和sumable_max或者0（0的意思就是甩掉上一个数字），如果新数字+sumable_max比positiveMax还高，就更新global_max；如果这个数字加进sumable_max大于0了，那对后续数字而言，加sumable_max是可以更大的（我在说什么，反正就是这个意思），否则不如直接重开。
找最小的子数组和时就完全反过来：保留全局最小和global_min+可加最小和sumable_min或0，如果新数字+sumable_min0那就白给，立刻重开。

时间复杂度$O(n)$，空间复杂度$O(1)$

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        global_max=0
        sumable_max=0
        global_min=0
        sumable_min=0
        for i in nums:
            sumable_max+=i
            global_max=max(global_max,sumable_max)
            sumable_max=max(0,sumable_max)
            
            sumable_min+=i
            global_min=min(global_min,sumable_min)
            sumable_min=min(0,sumable_min)
        return max(abs(global_max),abs(global_min))

官方Java代码：

class Solution {
    public int maxAbsoluteSum(int[] nums) {
        int positiveMax = 0, negativeMin = 0;
        int positiveSum = 0, negativeSum = 0;
        for (int num : nums) {
            positiveSum += num;
            positiveMax = Math.max(positiveMax, positiveSum);
            positiveSum = Math.max(0, positiveSum);
            negativeSum += num;
            negativeMin = Math.min(negativeMin, negativeSum);
            negativeSum = Math.min(0, negativeSum);
        }
        return Math.max(positiveMax, -negativeMin);
    }
}

3. 前缀和

前缀和指的是在数组最前面加个0（没这个的话一个子数组没法是最大的前缀和本身了），从第1个数字到当前数字的和，任何子数组和显然都是某2个前缀和的差值，最大的子数组和绝对值显然就是最大前缀和-最小前缀和

Python 3有内置函数：

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        s = list(accumulate(nums, initial=0))  # nums 的前缀和
        return max(s) - min(s)

Java实现的示例：

class Solution {
    public int maxAbsoluteSum(int[] nums) {
        int n=nums.length;
        int pre=0;
        int max=0;
        int min=0;
        for(int i=0;i<n;i++){
            pre+=nums[i];
            max=Math.max(max,pre);
            min=Math.min(min,pre);
        }
        return max-min;
    }
}