牛客周赛 Round 6

A 游游的数字圈

题目大意

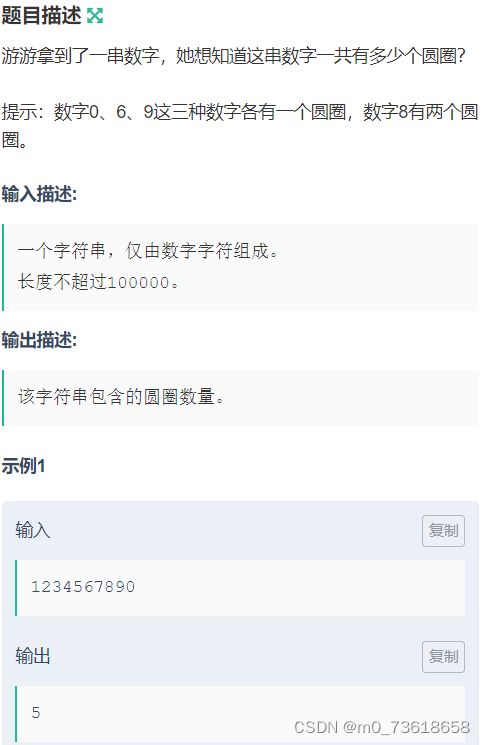
给定一个由数字字符组成的字符串，统计该字符串中出现的圆圈数量。其中数字0、6、9各有一个圆圈，数字8有两个圆圈。

思路分析

遍历字符串中的每个字符，对于每个字符，判断其是0、6、9则加1，是8则加2

时间复杂度

O(n)

AC代码

#include
using namespace std;
int main()
{
    string s;
    cin>>s; 
    int cnt=0; 
    for(char c:s) 
    {
        if(c=='0'||c=='6'||c=='9'){
            cnt++;
        }else if(c=='8'){
            cnt+=2;
        }
    }
    cout<<cnt<<endl; 
    return 0;
}

B 竖式乘法

题目大意

按照游游的竖式乘法计算a乘以b的值，并输出结果。

思路分析

游游给出的竖式乘法是一种按位相乘并相加的方法。对于每个位上的数，将a与b的对应位相乘，并将结果累加得到最终答案。

时间复杂度

O(t*m)

AC代码

#include
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int t;
    cin >> t;
    while(t--) {
        int a;
        string b;
        cin >> a >> b;
        long long res = 0;
        for(char c : b) {
            res += a * (c - '0');
        }
        cout << res << endl;
    }
    return 0;
}

C 游游的数值距离

题目大意

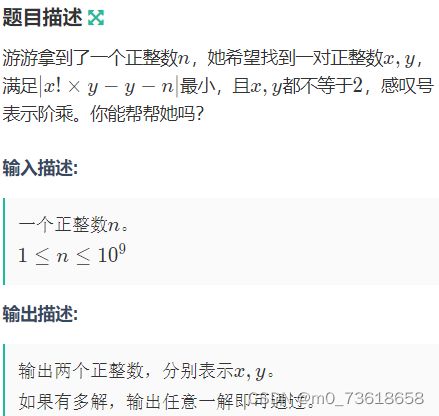
给定一个正整数n，找到一对正整数x和y，使得|x! × y - y - n|最小，并且x和y不能等于2。

思路分析

把式子整理一下可知，题目要求找到一个正整数x和一个正整数y，使得(x!-1)*y与输入的n的差值最小。知n,可以枚举x，因为x!会很大，算到15！左右即可。剩下一个未知数y，对于每个x，我们计算出y的三种可能取值：y=n/(x!-1)，y=n/(x!-1)+1，y=n/(x!-1)-1。
因为题目要求使得(x!-1)*y与输入的n的差值最小。

• 在整数除法中，n/(x!-1) 已经是最小的可能值了。如果我们再减去1，那么 (x!-1)*(y-1) 的值会比 n 小得更多，这会使得 |x!×y-y-n| 的值变大，而不是变小。
  所以只需要考虑 y=n/(x!-1) 和 y=n/(x!-1)+1 因为 y=n/(x!-1) 是 y 的最小可能值，而 y=n/(x!-1)+1 则是使得 (p-1)*y 的值刚好大于 n 的最小 y 值。所以只有这两种情况都可能使得 |x!×y-y-n| 的值最小。

时间复杂度

O(1)

AC代码

#include
using namespace std;
#define int long long
signed main()
{
    int n;
    cin >> n;
    int p = 2, x = 1, y = 1, ans = n;
    for(int i = 3; i <= 15; i++)
    {
        p *= i; 
        int y1 = n / (p - 1); // 计算商y1
        if(abs((p - 1) * y1 - n) < ans && y1 != 2)
            x = i, y = y1, ans = abs((p - 1) * y1 - n);
        if(abs((p - 1) * (y1 + 1) - n) < ans && y1 + 1 != 2)
            x = i, y = y1 + 1, ans = abs((p - 1) * (y1 + 1) - n);
    }
    cout << x << ' ' << y << endl;
    return 0;
}

D 游游的k-好数组

题目大意

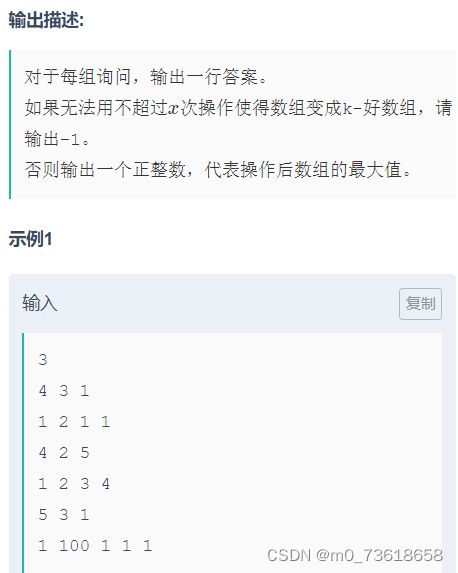
游游想要将一个大小为n的数组变成k-好数组，并且进行不超过x次操作。要求变换后的数组的最大值尽可能大。

思路分析

每个区间，滑动窗口每加一个t[i%k]，就要减一个t[i%k]，所以加和减要相等。记录每组元素中最大的元素为t[i%k]。

• 首先，可以将数组按照k的大小进行分组，每组的元素个数为n/k（如果n不能被k整除，那么前n%k组的元素个数为n/k+1）。
• 然后，计算每组的最大元素，并记录下来。同时，我们也计算出将每个元素变为其所在组的最大元素需要的操作次数，并累加起来。
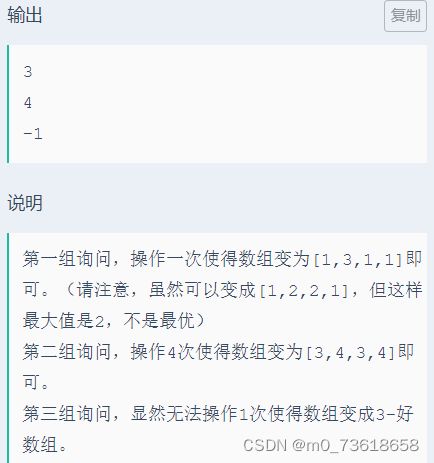
• 如果累加的操作次数大于x，那么说明无法在不超过x次操作的情况下使得数组变为k-好数组，输出-1。
• 如果累加的操作次数小于等于x，那么我们可以继续增大每组的最大元素。将剩余的操作次数平均分配给每组，然后将每组的最大元素增大相应的值。
• 最后，数组的最大值就是所有组的最大元素中的最大值。

时间复杂度

O(n)

AC代码

#include
using namespace std;
const int N=1e5+5;
int a[N],t[N];
void solve()
{
    memset(t,0,sizeof t);
    int n,k,x;
    cin>>n>>k>>x;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        t[i%k]=max(t[i%k],a[i]);
    }
    int cn=0;
    for(int i=0;i<n;i++)
    {
        cn+=t[i%k]-a[i];
    }if(x<cn)
    {
        cout<<-1<<"\n";
        return;;
    }
    x-=cn;
    int ans=0;
    for(int i=0;i<k;i++)
    {
        int rest=n/k+(i<n%k);
        ans=max(ans,t[i]+x/rest);
    }
    cout<<ans<<"\n";
}
signed main()
{
    int t;
    cin>>t;
    while(t--)
    {
        solve();
    }
    return 0;
}

E 小红的循环节长度

题目大意

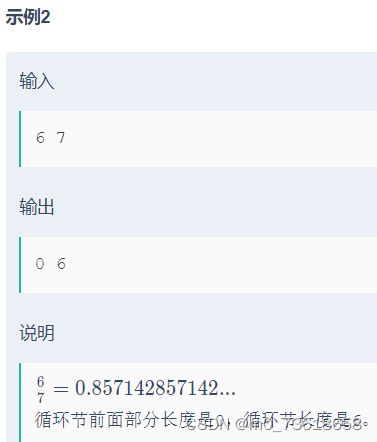
小红想知道一个分数的循环节前面部分的长度以及循环节的长度。给定两个正整数p和q，代表分子和分母。要求输出循环节前面部分的长度和循环节的长度。

思路分析

根据数学原理，一个分数可以表示为有限小数或无限循环小数。对于无限循环小数而言，循环节是必然存在的。通过欧拉函数和模运算，可以计算出循环节的长度。同时，通过化简分母为最简形式以及判断分数是否为有限小数，可以提前排除掉一部分情况，减少计算量。

• 首先判断给定的分数是否为有限小数。如果分母能够被2或5整除，则说明分数是有限小数，直接输出-1。
• 将分母化简为最简形式，并计算分母中包含2和5的个数，用c2和c5表示。
• 计算欧拉函数phi(q)，得到与q互质的小于等于q的正整数个数。
• 遍历phi(q)的所有因子i，判断10ⁱ和10^(phi(q)/i)在模q下是否为1，如果是则更新循环节长度mi为i或phi(q)/i的较小值。
• 输出max(c2, c5)作为循环节前面部分的长度，输出mi作为循环节的长度。

所用到的知识点和算法：

• 欧拉函数：用于计算与给定正整数互质的小于等于它的正整数个数。
• 快速幂算法：用于快速计算一个数的指定次幂，降低时间复杂度。
• 最大公约数：用于化简分数为最简形式。
• 模运算：用于判断10ⁱ和10^(phi(q)/i)在模q下是否等于1。

时间复杂度

O(sqrt(q) * sqrt(phi(q)) * log(q))

AC代码

#include
#define int long long
using namespace std;

// 欧拉函数
int phi(int x) {
    int res = x;
    for (int i = 2; i <= x / i; i++) {
        if (x % i == 0) {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    }
    if (x > 0) res = res / x * (x - 1);
    return res;
}

// 快速幂模运算
int qmi(int a, int k,int p) {
    __int128 res = 1;
    while (k)
    {
        if (k & 1) res =(__int128) res * a%p;
        a = (__int128)a*a%p;
        k >>= 1;
    }
    return res;
}

// 求最大公约数
int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

void solve() {
    int p, q;
    cin >> p >> q;
    
    // 约分并计算分母中包含的因子个数
    q /= gcd(p, q);
    int c2 = 0, c5 = 0;
    while (q % 2 == 0) q /= 2, c2++;
    while (q % 5 == 0) q /= 5, c5++;

    // 判断是否为有限小数
    if (q == 1) {
        cout << -1;
        return;
    }

    // 求解循环节前面部分长度和循环节长度
    int te= phi(q);
    int mi = 1e18;
    for (int i = 1; i <= te/ i; i++) {
        if (te% i == 0) {
            if (qmi(10, i, q) == 1)mi = min(mi, i);
            if (qmi(10, te/ i, q) == 1) mi = min(mi, te/ i);
        }
    }
    
    cout << max(c2, c5) << ' ' << mi;
}

signed main() {
    solve();
    return 0;
}