在正式开始之前，写一写自己的感受吧。
这是我在牛客打的第一场rating场，之前由于时间等原因，一直没有时间打，只能在赛后vp，昨天没有课，就打了一场，然后就过了一题，rating1054，牛客练习赛的难度还是比较高的...快要天梯赛了，要努力加油啊！
A：
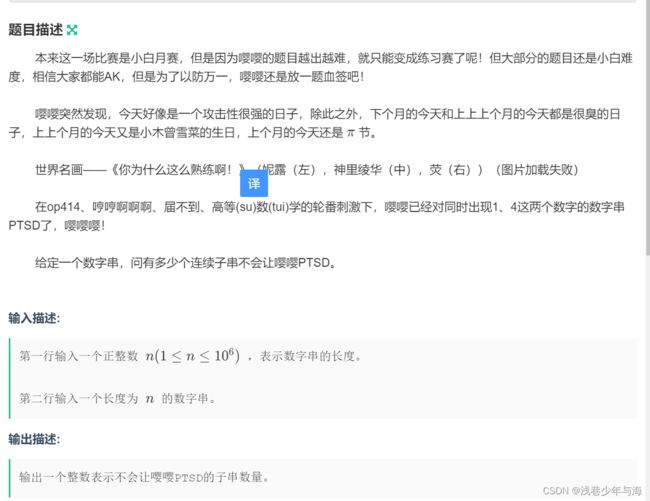
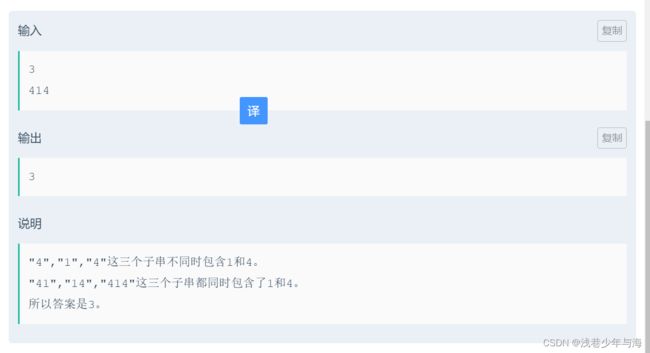题目有点长，但好多都是废话，简洁来说就是给你一个字符串，找到其中没有1和4的字串的个数
这道题我和这道题混淆了登录—专业IT笔试面试备考平台_牛客网，用了双指针，我蓝桥杯有道题也用了双指针，没出来...做了半天发现不对，然后想尝试别的方法，因为字符串的长度10^6,所以只能用单层循环，最后也没想出来优化；
正确思路：遍历字符串的长度，记录1和4最后出现的位置，用当前位置减去1和4最后出现位置的最小值再求和。
比如0010004，假设i现在在7位置，即在4的位置，字串有4，04，004，0004共4种。
代码如下：
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
感想：我是菜狗和懒狗，需要努力了..
B：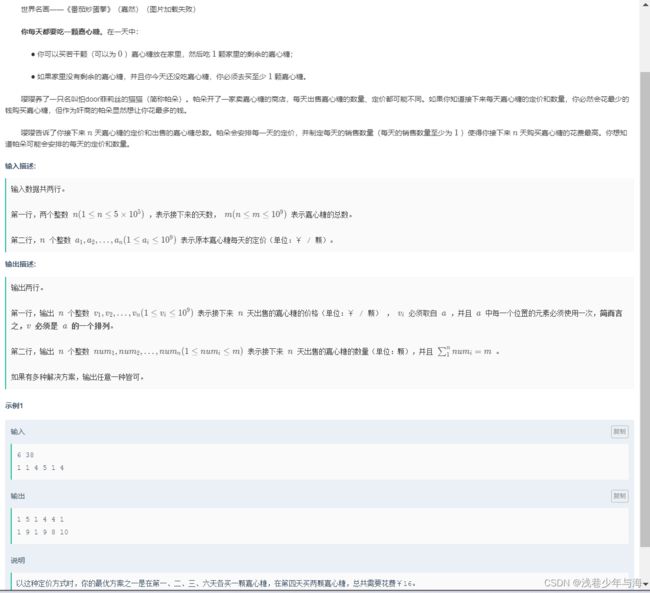
题目是真的长啊，废话连篇..
我感觉这道题才是真正的签到题，A题是啥啊...
理解了题意之后很好做，把夹心糖的价格从大到小排列，然后1-n-1天每天卖一块，第n天卖m-n+1即可
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
C：感觉好难，直接不做，也没补..
D：嘤嘤的可爱（easy）
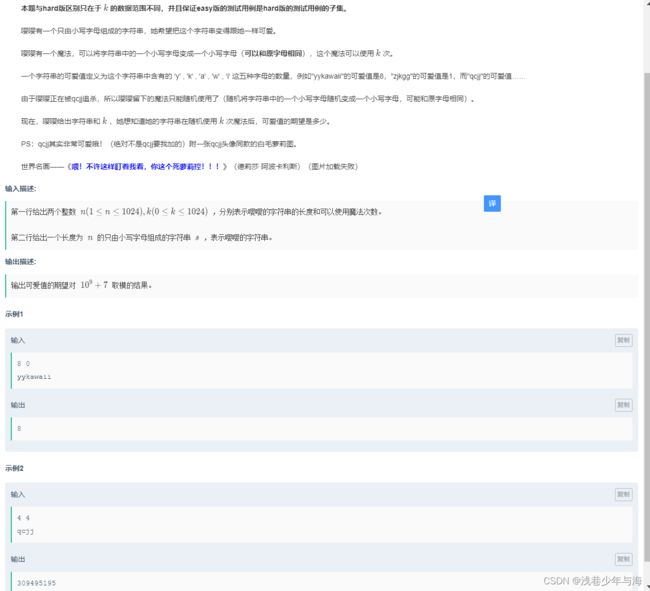题目又是好长，废话连篇，我除了AB之外就做了这题，觉得这题可以做；
我的思路是用全排列 ，先枚举变换的个数x（1<=x<=k），再先产生一个有x个1的01数组a，然后
用next-permutation()函数产生全排列，如果a[i]==1就代表改变，否则就不变，如果有x个数发生改变，就有x种可能，在 'y' , 'k' , 'a' , 'w' , 'i'的字符有0-x个，即Cx0+Cx1*5+Cx2*(5^2)..+.Cxx*(5^x),
好像不对...
正确解法：动态规划
设dp[i]为经过i次魔法的期望值，对于第一次操作，修改有贡献字符的概率为dp[0]/n，修改无贡献的字符的概率为（1-dp[i]）/n,对期望值产生影响的是将有贡献的字符改为无贡献字符，概率为21/26，将无贡献的字符改有贡献的字符，概率为5/26;
故状态表示：
dp[i]=dp[i-1]
dp[i] - =dp[i-1]/n*21/26
dp[i]+=(1-dp[i-1])/n*5/26
但是由于在运算过程中有除法，在运算过程中会有丢失数据，为了解决这一问题，可以用费马小定理，在此之前也不会，补题的过程中学了学...
费马小定理：费马小定理_小学生一发的技术成长之旅的博客-CSDN博客
同时·需要注意的是，由于减号的出现所以%mod的时候需要先加mod再%mod,即a=(a+mod)%mod;
代码如下：
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
E:
E是D的加强版，k到了long long的的范围了，n也到了10^6，用上题的方法，解不了，所以只能用别的方法了，结果就是个数学问题...
对于某个位置的字母，计算出被更改的可能性和不被更改的可能性，以及这两种可能性对可爱值的影响。
某一个位置没有被改变过的概率是 p0=（n-1/n）^k，被改变过的概率是p1=1-p0 。
若一个位置被多次改变，则只有最后一次改变有意义，改变成命运字母的概率是 t= 5/26。
因此，一个位置如果本来有贡献，那么这个位置有 p0 的概率不改变，贡献为 p0 ，若一个位置发生了改变，则有 t 的概率产生贡献，则贡献为 p1*t 。
注意点：减号！！
复杂度为O（n）
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
打完这场，发现自己是真的菜...，继续加油吧！！！
题解：题解 | #嘤嘤的签到#_牛客博客
