【非欧几里得域信号的信号处理】使用经典信号处理和图信号处理在一维和二维欧几里得域信号上应用低通滤波器研究(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
2.1 算例1
2.2 算例2
2.3 算例3
2.4 算例4
2.5 算例5
2.6 算例6
2.7 算例7
2.8 算例8
2.9 算例9
2.10 算例10
2.11 算例11
3 参考文献
4 Matlab代码实现
1 概述
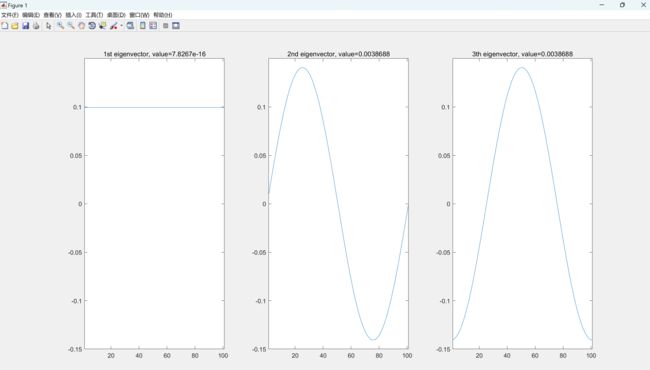
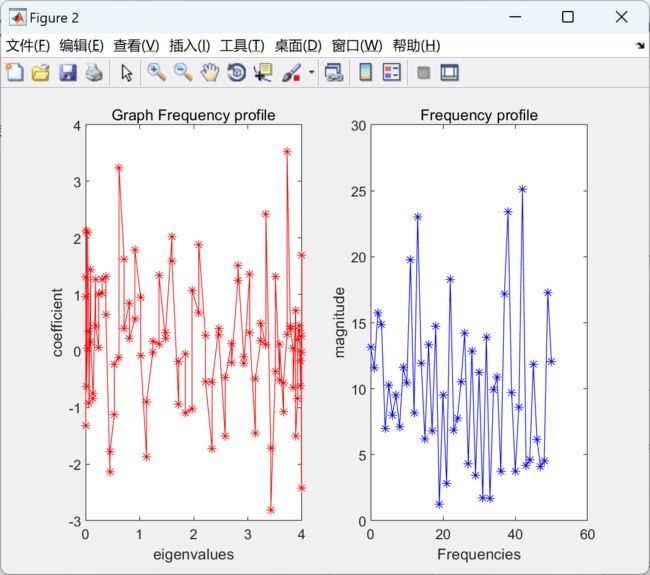
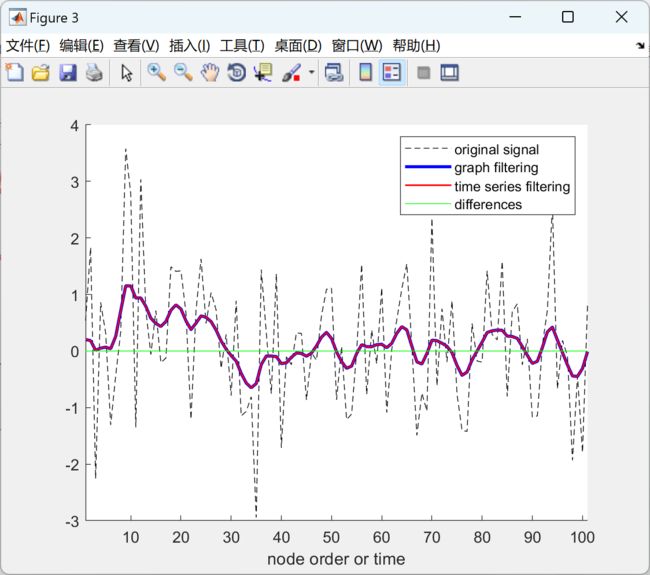
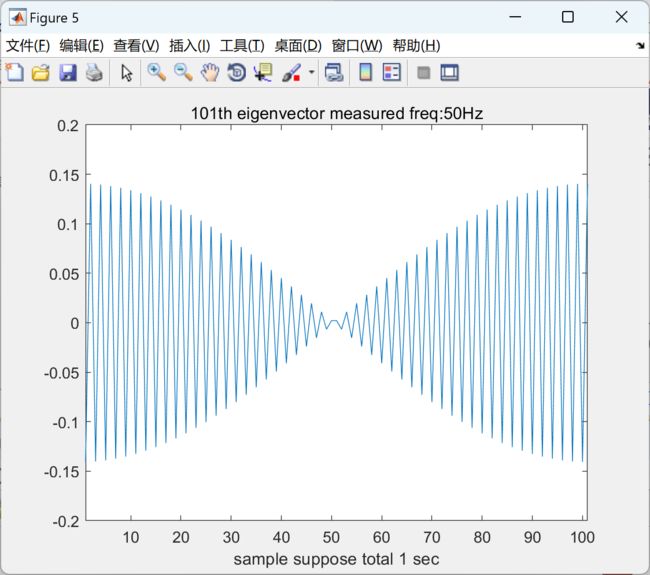
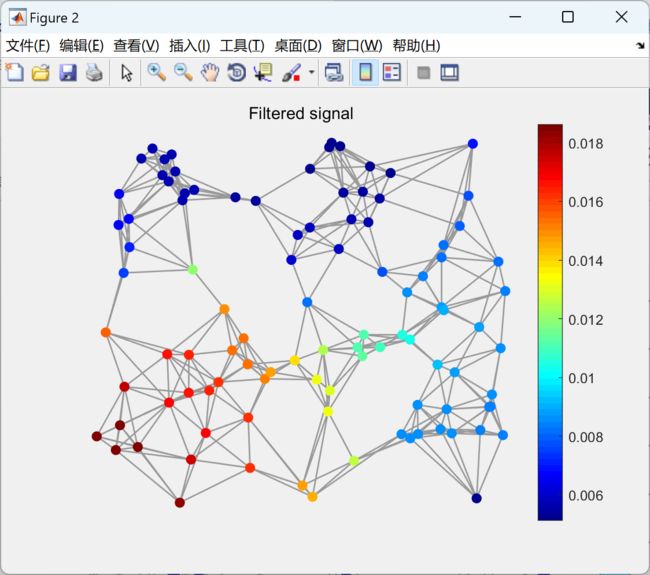
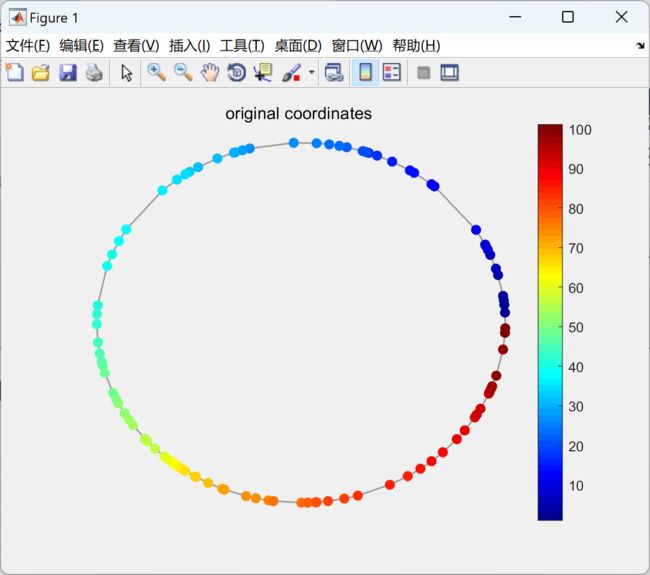
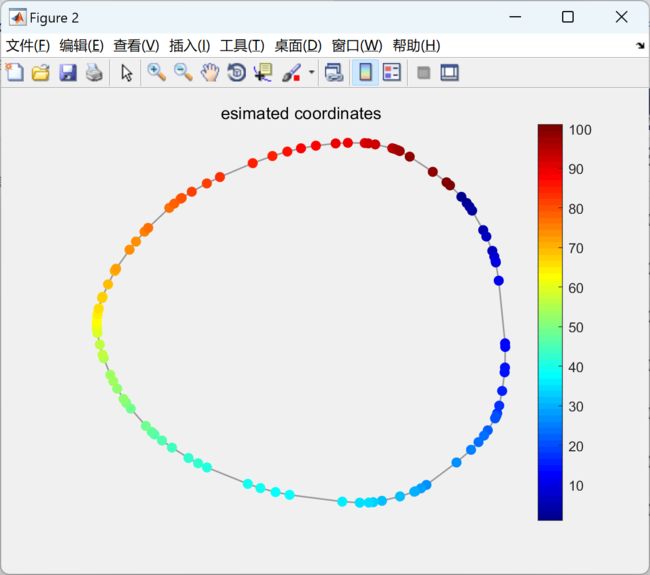
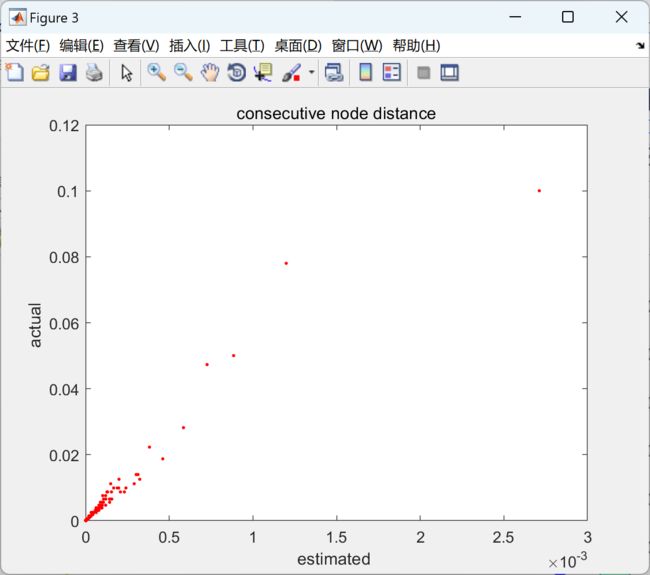
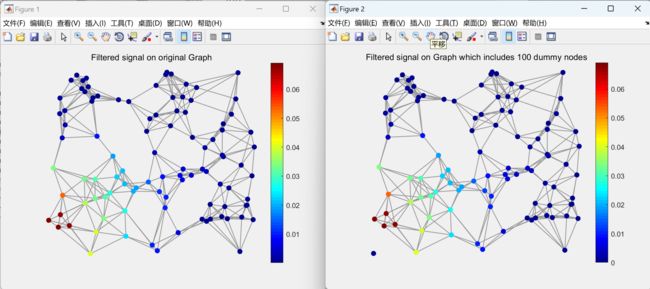
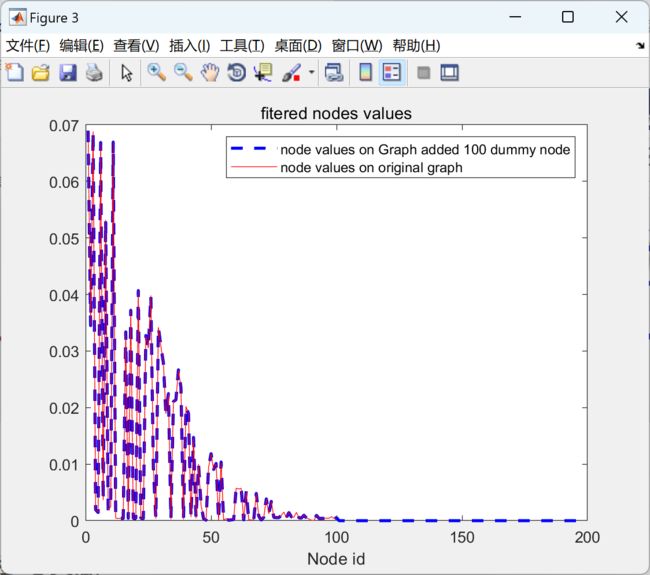
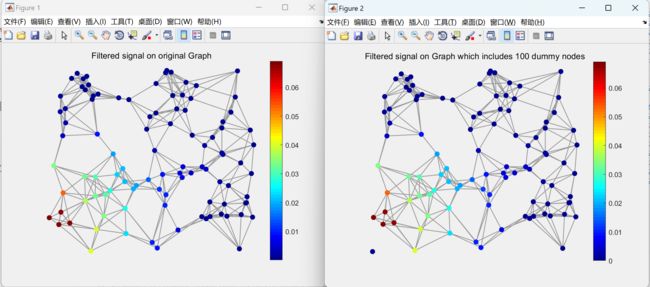
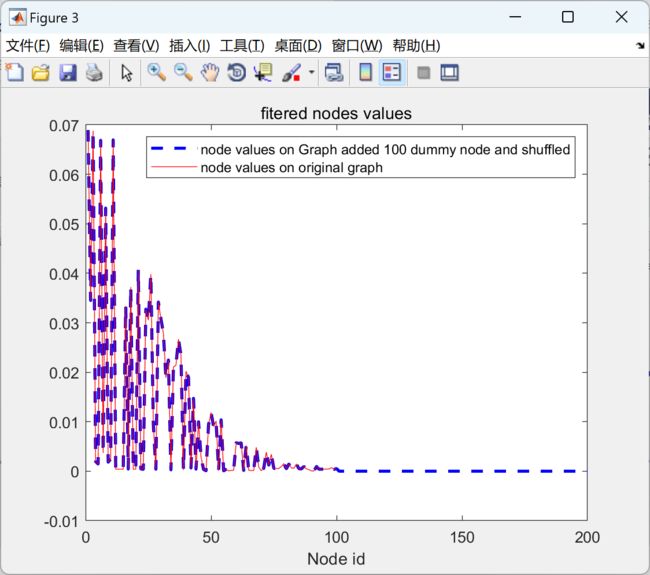
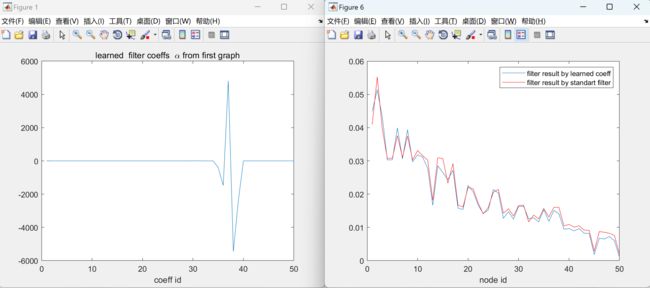
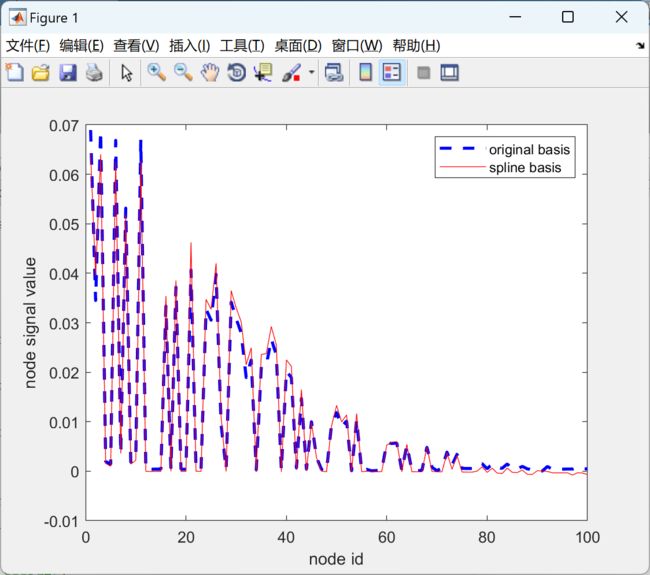
本文包括使用经典信号处理和图信号处理在一维和二维欧几里得域信号上应用低通滤波器,并比较两种结果是否相同。通过这种方式,我们将验证图信号处理的工作机制。此外,还展示了在非欧几里得域上对信号进行滤波的示例。
在信号处理领域,传统的信号处理方法通常假设信号存在于欧几里得空间中。然而,许多实际应用中的信号并不满足这个假设,因为它们存在于非欧几里得域中,如图结构、社交网络、脑连接等。因此,研究人员开始探索如何在非欧几里得域上进行信号处理,以更好地理解和分析这些信号。
本文旨在综合评估使用经典信号处理和图信号处理方法在一维和二维欧几里得域信号上应用低通滤波器的研究进展。低通滤波器是一种常用的信号处理工具,用于去除高频噪声和保留信号的低频成分。
经典信号处理方法在欧几里得域中广泛应用,如傅里叶变换、小波变换等。这些方法在一维和二维欧几里得域信号上应用低通滤波器已经被广泛研究和验证。然而,在非欧几里得域中应用这些方法可能会导致信息丢失或失真,因为这些方法没有考虑到非欧几里得域的特殊结构和连接关系。
为了解决这个问题,图信号处理方法被引入到非欧几里得域信号处理中。图信号处理是一种基于图结构的信号处理方法,它利用图模型来表示信号的连接关系和局部结构。通过在图域上定义低通滤波器,可以更好地保留非欧几里得域信号的结构和特征。
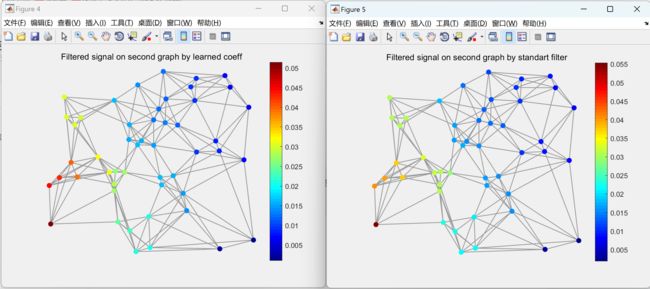
在研究中,我们将比较使用经典信号处理和图信号处理方法在一维和二维欧几里得域信号上应用低通滤波器的结果。我们将验证这两种方法是否能够产生相同的滤波效果,并评估它们对非欧几里得域信号的适应性和性能。
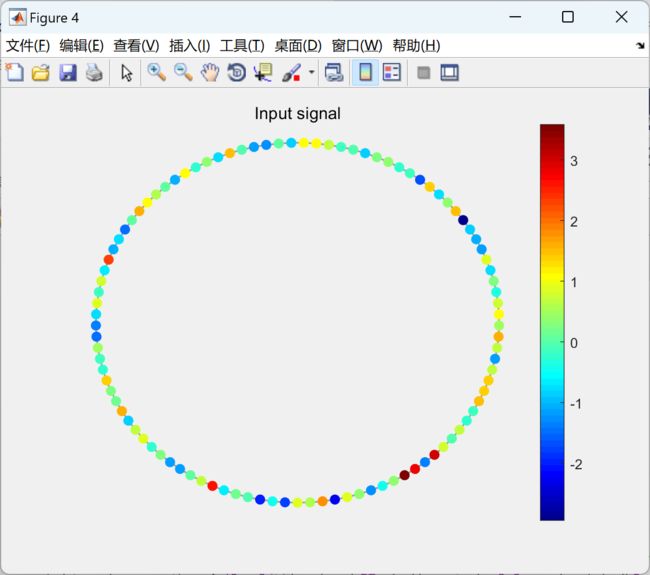
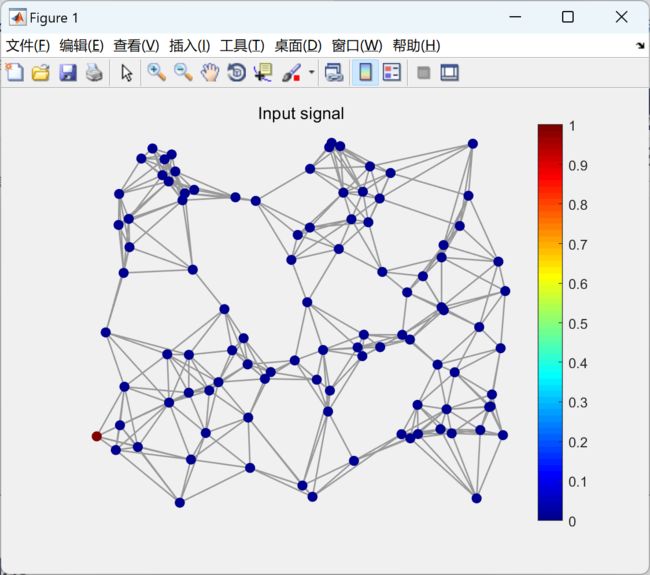
此外,我们还将介绍一个在非欧几里得域上对信号进行滤波的实例。通过这个实例,我们将展示图信号处理方法在处理非欧几里得域信号时的优势和应用潜力。
总之,本综述将为非欧几里得域信号的信号处理研究提供一个综合的概述,比较经典信号处理和图信号处理方法在一维和二维欧几里得域信号上应用低通滤波器的研究进展,并展示图信号处理方法在非欧几里得域信号处理中的应用示例。
2 运行结果
2.1 算例1
2.2 算例2
2.3 算例3
2.4 算例4
2.5 算例5
2.6 算例6
2.7 算例7
2.8 算例8
2.9 算例9
2.10 算例10
2.11 算例11
部分代码:
% load predefined W matrix for 100 nodes
load mydata
% calculate combinatorial Laplacian Matrix
d = sum(W,2);
L = diag(d)-W;
% calculate Laplacian Matrix
% find eigenvector and eigenvalues of combinatorial Laplacian
[u v]=eig(L);
% make eignevalue as vector
v=diag(v);
% get maximum eigenvalue
lmax=max(v);
v(v<0)=0;
% create signal where first node is 1 rest of them zero
s=zeros(size(W,1),1);
s(1)=1;
% determine filter
flt =exp(-20*v);
% apply that filter on to graph signal
sf=u*(flt.*(u'*s));
% determine filter by chebyshev
K=120;
nL=2*L/lmax-eye(size(L));
nu=chebyshev_basis(nL, s, K);
alpha=pinv(nu)*sf;
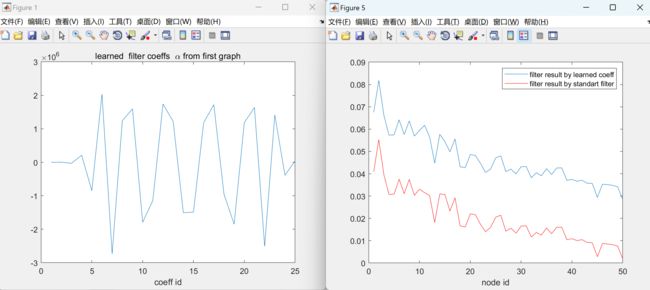
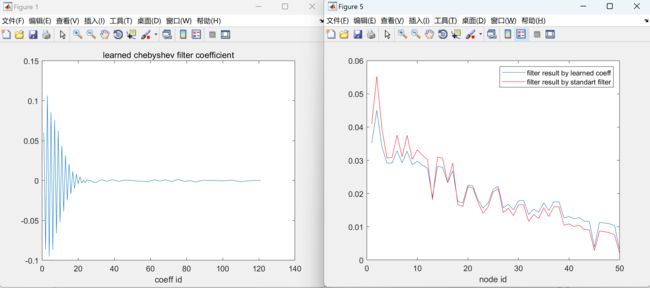
figure;plot(alpha)
xlabel('coeff id');
title('learned chebyshev filter coefficient')
% apply that filter on to graph signal
sf2=nu*alpha;
% visualize input and result
run gspbox/gsp_start
G=gsp_graph(W,coord);
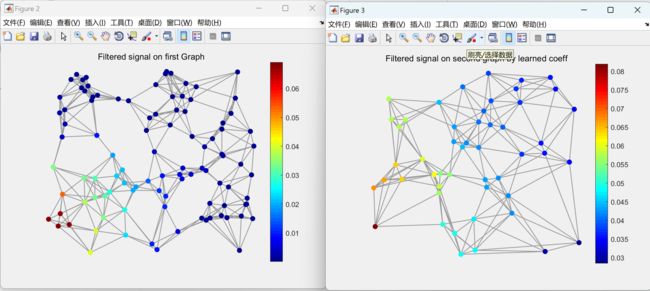
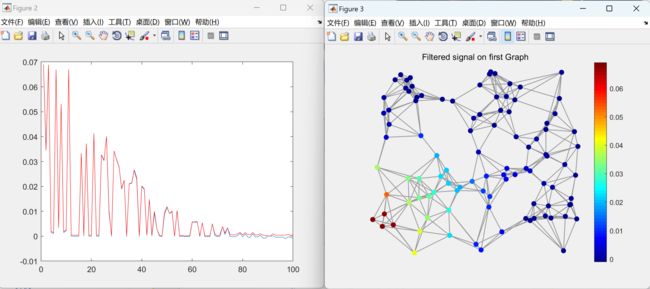
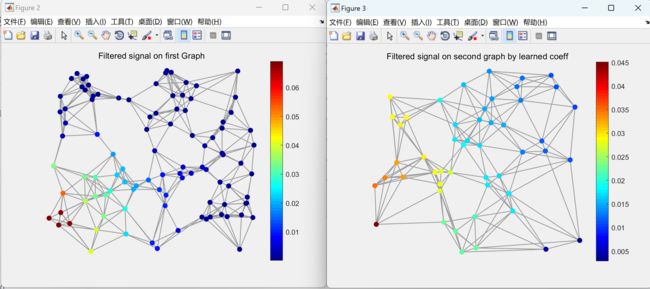
figure;gsp_plot_signal(G,sf2)
title('Filtered signal on first Graph');
load data2
% calculate combinatorial Laplacian Matrix
d = sum(WW,2);
L = diag(d)-WW;
% calculate Laplacian Matrix
% find eigenvector and eigenvalues of combinatorial Laplacian
[u v]=eig(L);
% make eignevalue as vector
v=diag(v);
% get maximum eigenvalue
lmax=max(v);
v(v<0)=0;
% create signal where first node is 1 rest of them zero
s=zeros(size(WW,1),1);
s(1)=1;
% determine filter
nL=2*L/lmax-eye(size(L));
nu=chebyshev_basis(nL, s, K);
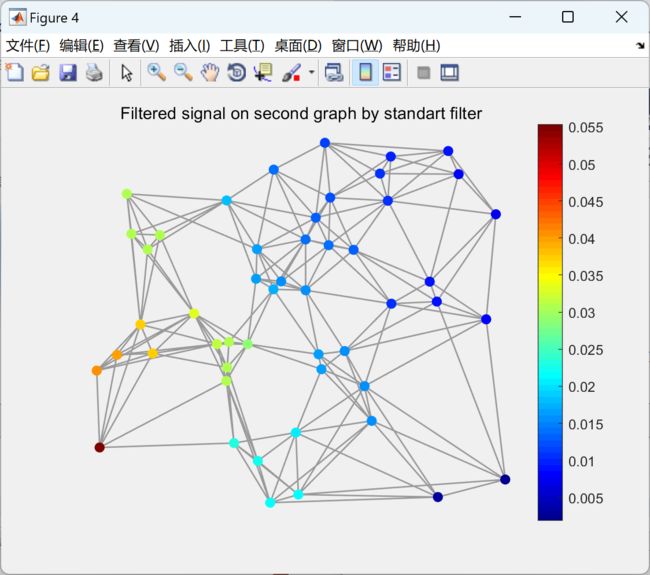
% apply that filter on to graph signal
sf2=nu*alpha;
3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]吴一全,朱兆达.一维与二维信号的快速内插算法[J].南京航空航天大学学报, 1995, 27(2):9.DOI:CNKI:SUN:NJHK.0.1995-02-006.
[2]宣琦,项靖阳,崔慧,等.一种融合一维二维卷积神经网络的深度学习信号分类方法:CN202010736397.6[P].CN112069883A[2023-08-04].
[3]王群,姚为正,王兆安.高通和低通滤波器对谐波检测电路检测效果的影响研究[J].电工技术学报, 1999, 14(5):5.DOI:10.3321/j.issn:1000-6753.1999.05.006.
[4]赵晓群,张洁.巴特沃斯低通滤波器的实现方法研究[J].大连民族学院学报, 2013.DOI:CNKI:SUN:DLMY.0.2013-01-017.