每天一道leetcode：剑指 Offer 04. 二维数组中的查找（中等&二分查找）

今日份题目：

在一个 n * m 的二维数组中，每一行都按照从左到右 非递减 的顺序排序，每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

提示

0 <= n <= 1000
0 <= m <= 1000

题目思路及代码

方法一：暴力搜索

遍历每行每列的所有元素查找有无target。

双重循环，时间复杂度为O(n*m)。

代码

class Solution 
{
public:
    bool findNumberIn2DArray(vector>& matrix, int target) 
    {
        int n=matrix.size();
        if(n==0) return false;
        int m=matrix[0].size();
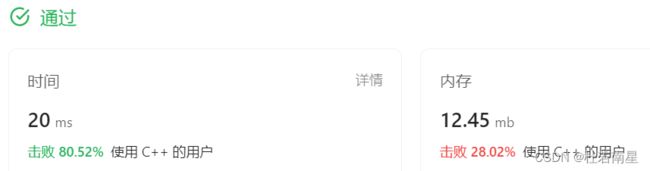
        for(int i=0;i

提交结果

方法二：二分查找

对每行进行二分查找。

行单循环，二分查找时间复杂度为O(logm)；故，总时间复杂度为O(nlogm)。

代码

class Solution 
{
public:
    bool find(vector>& matrix,int target,int row)//二分查找函数
    {
        int n=matrix[0].size();
        int l=0,r=n-1,mid;
        while(l<=r)
        {
            mid=(l+r)/2;
            if(matrix[row][mid]==target) return true;
            else if(matrix[row][mid]>target)
            {
                r=mid-1;
            }
            else l=mid+1;
        }
        return false;
    }

    bool findNumberIn2DArray(vector>& matrix, int target) 
    {
        int n=matrix.size();
        if(n==0) return false;
        bool ans;
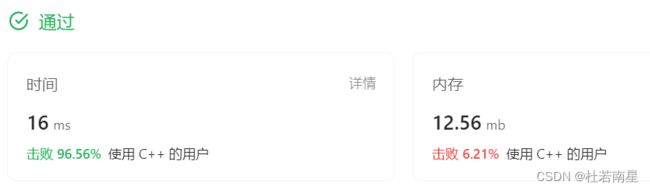
        for(int i=0;i

提交结果

方法三：Z型查找（官方给出的）

根据题目说到的数据特点，Z型查找。即为，如果当前元素比target大，就往左找；如果当前元素比target小，就往下找。

代码

class Solution 
{
public:
    bool findNumberIn2DArray(vector>& matrix, int target) 
    {
        int n=matrix.size();
        if(n==0) return false;
        int m=matrix[0].size();
        int x=0,y=m-1;//从右上角开始查找
        while(x=0) //到左下角
        {
            if(matrix[x][y]==target) return true;
            if(matrix[x][y]>target) y--;//大了，往左找
            else x++; //小了，往下找
        }
        return false;
    }
};

提交结果

提交结果可能随着提交次数的改变而改变，大家不用太焦虑这个结果，重点是掌握方法和知道其对应的时间复杂度。 

欢迎大家在评论区讨论，如有不懂的代码部分，欢迎在评论区留言！