LeetCode高频题56. 合并区间，将重叠的区间合并为一个区间，包含所有区间

LeetCode高频题56. 合并区间，将重叠的区间合并为一个区间，包含所有区间

提示：本题是系列LeetCode的150道高频题，你未来遇到的互联网大厂的笔试和面试考题，基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们，吃完饭就是设计考题，然后去考应聘人员，你要做的就是学基础树结构与算法，然后打通任督二脉，以应对波云诡谲的大厂笔试面试题！
你要是不扎实学习数据结构与算法，好好动手手撕代码，锻炼解题能力，你可能会在笔试面试过程中，连题目都看不懂！比如华为，字节啥的，足够让你读不懂题

基础知识：
【1】线段最大重合问题：最多有多少条线段是重合的

---

题目

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/merge-intervals
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

一、审题

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2：

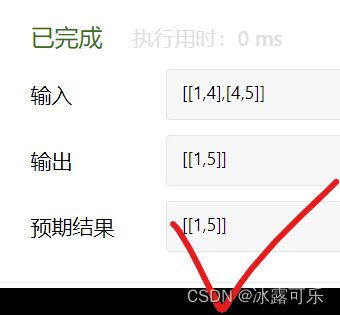
输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104

---

二、解题

之前讲过的最大线段重合问题，很相似的
基础知识：
【1】线段最大重合问题：最多有多少条线段是重合的
当时那个线段就是看看谁影响了我？？？？
我就要把它统计出来，这个题也是一样，相互影响，相互重合，融合即可

线段，按照start排序升序【用一个比较器，很容易干这事】

（0）这样，初始化s=s0,e=e0
下面这几段的话，初始化s=1,e=5
依次遍历后头的那些线段们
（1）来一个新的线段，看看我们俩重合了吗？重合的话，合并end，e等于当前最大的end
（2）如果不重合，则生成一段合并区间，就是刚刚s–e就是一个答案，然后s和e赋值为当前新线段的start和end，为下一次新的结果做准备

这么做其实就是贪心，我要把可能重合的线段们，整一堆，方便合并，
只要第二段的start>end前一段，那就没法合并，不重合呗
如果第二顿的start<=end前一段，那就是重合，需要合并，看看两端end谁大，就是合并之后的end

这是非常非常简单的一个贪心思想，贪心就意味着排序

看上图，1–5这段，初始化s=1,e=5
看上图，1–4这段，1并没有大于e=5，则俩重合，那end取max（4,5）=5
看上图，1–6这段，1并没有大于e=5，则俩重合，那end取max（6,5）=6
看上图，2–4这段，2并没有大于e=6，则俩重合，那end取max（6,4）=6
看上图，3–9这段，3并没有大于e=6，则俩重合，那end取max（6,9）=9
看上图，12–14这段，12大于e=9，则俩不重合，那必须生成一个合并的结果，s=1,9
重新赋值s=12，e=14，继续看后面的线段

情况就是这样了

排序复杂度o(nlog(n))
遍历整理答案，o(n)
故本题复杂度看排序的复杂度

手撕代码试试：

把区间包装为节点node，顺便整一个比较器cptr：按照start升序排列即可

        public static class cptr implements Comparator<Node>{
            @Override
            public int compare(Node o1, Node o2){
                return o1.start - o2.start;
                //start升序——之前还想让end降序，不需要
            }
        }

        public static class Node{
            public int start;
            public int end;

            public Node(int s, int e){
                start = s;
                end = e;
            }
        }

然后手撕本题代码

这儿唯一要主要的几个点：
第一，如果N=1，那很OK，就返回arr即可

第二，当你遍历到N-1那个数组时
我不管你是重合合并了区间，还是不重合收集了前面的答案
N-1这个区间所在的答案时没有被收集的
因此，要单独收集这个区间

第三，咱们也不知道到底有多少个结果，所以呢，需要中途把结果放入动态数组，最后用静态数组转，返回就行

        //这个方法可以做，但是超出时限了，看来还需要优化！！！
        public int[][] merge(int[][] intervals) {
            if (intervals == null || intervals.length == 0) return null;
            int N = intervals.length;
            if (N == 1) return intervals;//一个就算了吧
            //（0）这样，初始化s=s0,e=e0
            //下面这几段的话，初始化s=1,e=5
            //依次遍历后头的那些线段们
            //（1）来一个新的线段，看看我们俩重合了吗？重合的话，合并end，e等于当前最大的end
            //（2）如果不重合，则生成一段合并区间，就是刚刚s--e就是一个答案，然后s和e赋值为当前新线段的start和end，为下一次新的结果做准备
            //先将数组——转化为节点数组，排序
            Node[] arr = new Node[N];
            for (int i = 0; i < N; i++) {
                arr[i] = new Node(intervals[i][0], intervals[i][1]);//造节点，升序排列
            }
            Arrays.sort(arr, new cptr());

            //准备收集答案
            int s = arr[0].start;
            int e = arr[0].end;
            //先搞动态数组，然后将其转化为静态数组返回
            ArrayList<List<Integer>> ans = new ArrayList<>();
            for (int i = 1; i < N; i++) {
                int start = arr[i].start;
                int end = arr[i].end;
                //看看重叠吗？
                if (start <= e) {//重叠
                    e = Math.max(e, end);//看谁大，就是合并的end
                }else {//start > e那收集结果，新开区间
                    List<Integer> tmp = new ArrayList<>();
                    tmp.add(s);
                    tmp.add(e);
                    ans.add(tmp);//算一个结果
                    s = start;
                    e = end;//从新开一个可能的合并区间
                }
                //有个小问题就是最后一个元素处理完，可能还需要检查
                if (i == N - 1){
                    //不管如何呢，这最后的区间肯定是没有被放进去的，还需要手动放最后一个
                    List<Integer> tmp = new ArrayList<>();
                    tmp.add(s);
                    tmp.add(e);
                    ans.add(tmp);//算一个结果
                }
            }
            int M = ans.size();//结果，转静态数组
            int[][] res = new int[M][2];
            for (int i = 0; i < M; i++) {
                res[i][0] = ans.get(i).get(0);
                res[i][1] = ans.get(i).get(1);//s--e
            }

            return res;
        }

看里面的if else条件，你就知道
如果N-1那个区间，需要跟前面合并，，就是合并而已，跳过哦了else就没有加入结果
如果N-1那个区间，不需要合并，跳过了if，去了else，但是即使如此，咱们生成的结果也是前面的，N-1这个区间重新赋值给s和e也没有被加入结果
因此需要判断N-1这个地方，无论咋着咱都要把最后这个s和e生成一个答案放入结果

测试一把：

    public static void test(){
        int[][] arr = {
                {1,3},
                {2,6},
                {8,10},
                {15,18}
        };

        Solution solution = new Solution();
        int[][] ans = solution.merge(arr);
        for (int i = 0; i < ans.length; i++) {
            for (int j = 0; j < ans[0].length; j++) {
                System.out.print(ans[i][j] +" ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        test();
    }

1 6 
8 10 
15 18 

LeetCode测试：

---

总结

提示：重要经验：

1）这个题，涉及区间，线段，重合问题，就是考虑要排序的事情，贪心解决，要么排序start，要么排序end，反正要想办法用贪心搞定
2）中途关键的地方，就是融合区间到N-1那，最后那个区间是没有被加入结果的，所以自己捣鼓清楚
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。