【统计学】Python计算并绘制样本数据的经验分布函数
参考文献:
一篇绘制累积经验分布函数图像的博客
如何得到样本数据的经验分布函数?
from statsmodels.distributions.empirical_distribution import ECDF
ecdf = ECDF([3,3,1,4]) # 返回了一个分布函数,我是说数学书上的函数
type(ecdf)
Out[19]: statsmodels.distributions.empirical_distribution.ECDF
ecdf(3) # 往这个分布函数中输入自变量,会得到其分布函数值
Out[20]: 0.75
ecdf(1)
Out[21]: 0.25
help(ECDF) # 看看介绍,我也没太懂。。。
Help on class ECDF in module statsmodels.distributions.empirical_distribution:
class ECDF(StepFunction)
| ECDF(x, side='right')
|
| Return the Empirical CDF of an array as a step function.
|
| Parameters
| ----------
| x : array_like
| Observations
| side : {'left', 'right'}, optional
| Default is 'right'. Defines the shape of the intervals constituting the
| steps. 'right' correspond to [a, b) intervals and 'left' to (a, b].
|
| Returns
| -------
| Empirical CDF as a step function.
|
| Examples
| --------
| >>> import numpy as np
| >>> from statsmodels.distributions.empirical_distribution import ECDF
| >>>
| >>> ecdf = ECDF([3, 3, 1, 4])
| >>>
| >>> ecdf([3, 55, 0.5, 1.5])
| array([ 0.75, 1. , 0. , 0.25])
|
| Method resolution order:
| ECDF
| StepFunction
| builtins.object
|
| Methods defined here:
|
| __init__(self, x, side='right')
| Initialize self. See help(type(self)) for accurate signature.
|
| ----------------------------------------------------------------------
| Methods inherited from StepFunction:
|
| __call__(self, time)
| Call self as a function.
|
| ----------------------------------------------------------------------
| Data descriptors inherited from StepFunction:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
绘制样本的经验分布函数
方法一:
博客原文
# 这也是借鉴别人博客的代码,我再补充点自己的看法
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
datas = np.array([64.3, 65.0, 65.0, 67.2, 67.3, 67.3, 67.3, 67.3, 68.0, 68.0, 68.8, 68.8, 68.8, 69.7,\
69.7, 69.7, 70.3,70.4, 70.4, 70.4, 70.4, 70.4,70.4, 70.4, 71.2, 71.2, 71.2, 71.2,\
72.0, 72.0, 72.0, 72.0, 72.0, 72.0, 72.0, 72.7, 72.7, 72.7, 72.7, 72.7, 72.7, 72.7,\
73.5, 73.5, 73.5, 73.5, 73.5, 73.5, 73.5, 73.5, 73.5,73.5, 73.5, 74.3, 74.3, 74.3,\
74.3, 74.3, 74.3, 74.3, 74.3, 74.7, 75.0, 75.0, 75.0, 75.0, 75.0, 75.0, 75.0, 75.4,\
75.6, 75.8, 75.8, 75.8, 75.8, 75.8, 76.5, 76.5, 76.5, 76.5, 76.5, 76.5, 76.5, 77.2,\
77.2,77.6, 78.0, 78.8, 78.8, 78.8, 79.5, 79.5, 79.5, 80.3, 80.5, 80.5, 81.2, 81.6,\
81.6, 84.3])
#数据特征计算
s = np.std(datas, ddof=1)#样本标准差
xbar = np.mean(datas)#样本均值
#数据可视化 画数据经验分布曲线图
nt, bins, patches = plt.hist(datas, bins=10, histtype='step', \
cumulative=True, density=True, color='darkcyan')#datas是数据,bins是分组数
plt.title('bins = 10')
plt.savefig('经验函数分布图1.jpg', dpi=200)
plt.show()
#数据可视化 画数据经验分布曲线图
nt, bins, patches = plt.hist(datas, bins=15, histtype='step', \
cumulative=True, density=True, color='darkcyan')#datas是数据,bins是分组数
plt.title('bins = 15')
#正态分布函数曲线拟合
y = (1 / (np.sqrt(2 * np.pi) * s)) * np.exp(-0.5 * ((bins - xbar) ** 2 / s ** 2))
y = y.cumsum()
y = y / y[-1]
plt.plot(bins, y, 'tomato', linewidth = 1.5, label = 'Theoretical')
plt.savefig('经验函数分布图2.jpg', dpi=200)
plt.show()
# 这种方法有点奇怪,指定bins参数之后,就不能说绘制出来的经验分布函数是原样本的经验分布函数了
# 自己试试看,图太多了不方便一一往上贴,看看返回数组
plt.hist([3,3,1,4],histtype='step',cumulative=True,density=True)
Out[25]:
(array([0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.75, 0.75, 0.75, 1. ]),
array([1. , 1.3, 1.6, 1.9, 2.2, 2.5, 2.8, 3.1, 3.4, 3.7, 4. ]),
[<matplotlib.patches.Polygon at 0x14fb356be20>])
plt.hist([3,3,1,4],histtype='step',cumulative=True) # 没有density参数表示计数,而非计算频率
Out[26]:
(array([1., 1., 1., 1., 1., 1., 3., 3., 3., 4.]),
array([1. , 1.3, 1.6, 1.9, 2.2, 2.5, 2.8, 3.1, 3.4, 3.7, 4. ]),
[<matplotlib.patches.Polygon at 0x14fb4c47d90>])
plt.hist([3,3,1,4],histtype='step',cumulative=True,bins=4,density=True)
Out[28]:
(array([0.25, 0.25, 0.75, 1. ]),
array([1. , 1.75, 2.5 , 3.25, 4. ]),
[<matplotlib.patches.Polygon at 0x14fb6e5bb20>])
plt.hist([3,3,1,4],histtype='step',cumulative=True,bins=3,density=True)
Out[29]:
(array([0.25, 0.25, 1. ]),
array([1., 2., 3., 4.]),
[<matplotlib.patches.Polygon at 0x14fb4c31850>])
plt.hist([3,3,1,4],histtype='step',cumulative=True,bins=5,density=True)
Out[30]:
(array([0.25, 0.25, 0.25, 0.75, 1. ]),
array([1. , 1.6, 2.2, 2.8, 3.4, 4. ]),
[<matplotlib.patches.Polygon at 0x14fb4c37820>])
# 也就是说,bins参数是平均分原数据的份数。由原数据的最大值和最小值以及bins参数共同决定各个子区间的范围。
方法二:
from statsmodels.distributions.empirical_distribution import ECDF
x = [3,3,1,4]
ecdf = ECDF([3,3,1,4])
type(ecdf)
Out[37]: statsmodels.distributions.empirical_distribution.ECDF
y = ecdf(x) # 计算分布函数值
x.sort()
x
Out[43]: [1, 3, 3, 4]
y.sort()
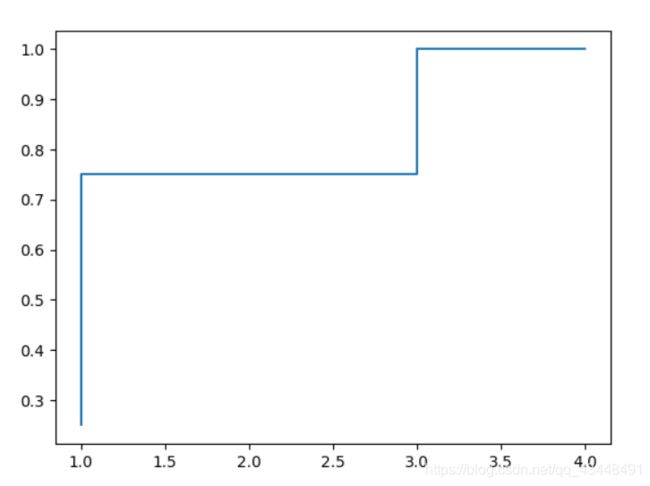
# 画阶梯函数之前一定要记得排序,不然就是乱七八糟的回字形
plt.step(x,y)
Out[45]: [<matplotlib.lines.Line2D at 0x14fc03b6850>]