408数据结构考研笔记——第三章栈、队列和数组
目录
一、栈
1.定义
2.相关概念
3.相关操作
1.顺序栈
2.共享栈
3.链栈
4.课后练习
二、队列
1.定义
2.相关概念
3.相关操作
1.顺序队列
2.链式队列
3.双端队列
三、栈和队列的应用
1.栈——括号匹配
2.栈——表达式求值
计算方法(计算机算法,毕竟咱人不搞这些奇怪运算):
转换关系(理论,不涉及代码):
计算机计算方法:
3.栈——递归
4.队列应用
四、数组和特殊矩阵
1.常用数组
2.特殊矩阵
1.对称矩阵的压缩存储
2.三角矩阵的压缩存储
3.三对角矩阵的压缩存储
4.稀疏矩阵的压缩存储
五、课后习题
一、栈
1.定义
只允许在一端进行插入或删除操作的线性表(本质 LIFO)。
2.相关概念
栈顶(top):线性表允许进行插入删除那一端。
栈底(bottom):固定的,不允许操作那一端。
空栈:不含任何元素。
3.相关操作
InitStack(&S):初始化
StackEmpty(S):判空
Push(&S, x):进栈
Pop(&S, &x):出栈,共![]() 种出栈顺序
种出栈顺序
GetTop(S, &x):读取栈顶元素
DestroyStack(&S):销毁栈
1.顺序栈
初始化
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int top;
}SqStack;
void InitStack(SqList &S)
{
S.top = -1;
}
int main()
{
SqStack S;
InitStack(S);
}判空
bool StackEmpty(SqStack S)
{
return (S.top == -1) ? true : false;
}进栈
bool Push(SqStack &S, ElemType x)
{
if(S.top == MaxSize - 1) return false;
S.data[++top] = x;
return true;
}出栈
bool Pop(SqStack &S, ElemType &x)
{
if(S.top == -1) return false;
x = S.data[top--];
return true;
}读取栈顶元素
bool GetTop(SqStack S, ElemType &x)
{
if(S.top == -1) return false;
x = S.data[S.top];
return true;
}2.共享栈
定义:设置两个栈共享一片空间,两个栈顶初始分别位于空间两端,向内部移动
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int top1;
int top2;
}ShStack;
void InitHStack(ShStack &S)
{
S.top1 = -1;
S.top2 = MaxSize; //栈满:top1+1 = top2
}3.链栈
定义:利用链表头插法进行入栈操作,利用头删法进行出栈。
typedef struct Linknode{
ElemType data;
struct Linknode *next;
}Linknode, *LiStack; //具体实现操作参考链表章节
4.课后练习
啦啦明天再写了,今天太晚了~
二、队列
1.定义
操作受限的线性表,只允许在表的一端进行插入,在另一端进行删除(先进先出 FIFO)
2.相关概念
队头(Front):允许删除的一端
队尾(Rear):允许插入的一端
空队列:元素数为0
3.相关操作
InitQueue(&Q):初始化队列
QueueEmpty(Q):判空
EnQueue(&Q, x):插入(入队)
DeQueue(&Q, &x):删除(出队)
GetHead(Q, &x):获取队首元素
1.顺序队列
利用数组和两个指针进行相关操作,注意操作针对的是“循环队列”,即将队列想象成一个环性箱格结构,根据不同的题目要求和习惯,队首队尾指针有不同的关系和操作方法,主要包括:
(1)队首队尾间隔一个元素距离,即队满时有一个缓冲空间,此时队满(rear+1)%MaxSize = front,队空rear = front,队内元素个数(rear+MaxSize-front)%MaxSize
(2)队首队尾没有元素空隙,即队满时两个指针指向同一元素,此时有两种处理方法:
i 设置辅助变量,如记录上一操作内容是插入还是删除来判断(rear+1)%MaxSize = front是队满还是队空情况,如果上次是插入(如标记位记为0)则是队满,若为删除(如标记位为1)则为队空
ii 设置辅助变量,记录队列中元素个数,队空size==0,队满size==MaxSize, 对内元素个数size
(3)rear初始在data[1]的位置,先插入后移动(前面rear初始在data[0]是先移动后插入),代码相似,只是操作顺序不同,不多赘述
总结:队列要么是牺牲一个元素空间,要么增加一个空间放置辅助变量
代码实现:
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int front;
int rear;
}SqQueue;
//若为情况二
//第一种,状态位控制
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int front;
int rear;
int state; //标志位,0为上一操作是插入,1为上一操作是删除
}SqQueue;
//第二种,记录元素个数
#define MaxSize 10
typedef struct{
ElemType data[MaxSize];
int front;
int rear;
int size;
}SqQueue;
//初始化
void InitQueue(SqQueue &Q)
{
Q.front = Q.rear = 0;
//size = 0; //针对情况二第二种情况
}
判空:
//情况一,有一个缓冲空间
bool QueueEmpty(SqQueue Q)
{
return (Q.rear == Q.front) ? true : false;
}
//情况二,没有缓冲空间
//第一种,有状态位
bool QueueEmpty(SqQueue Q)
{
return (Q.rear = Q.front && Q.state = 1) ? true : false;
}
//第二种,记录长度
bool QueueEmpty(SqQueue Q)
{
return (Q.size = 0) ? true : false;
}入队:
//情况一有缓冲空间
bool EnQueue(SqQueue &Q, ElemType x)
{
if((Q.rear+1)%MaxSize == Q,front) return false; //区别仅在判断队满条件不同
Q.data[Q.rear] = x;
Q.rear = (Q.rear+1) % MaxSize;
return true;
}
//情况二无缓冲空间
//第一种有状态位
bool EnQueue(SqQueue &Q, ElemType x)
{
if(Q.rear == Q,front && Q.state = 0) return false;
Q.data[Q.rear] = x;
Q.rear = (Q.rear+1) % MaxSize;
Q.state = 0;
return true;
}
//第二种记录长度
bool EnQueue(SqQueue &Q, ElemType x)
{
if(Q.size == MaxSize) return false;
Q.data[Q.rear] = x;
Q.rear = (Q.rear+1) % MaxSize;
Q.size++;
return true;
}
出队:
bool DeQueue(SqQueue &Q, ElemType &x)
{
if(QueueEmpty(Q)) return false; //这里直接使用了判空函数,就不多写不同情况的判空了
x = Q.data[Q.front];
Q.front = (Q.front+1)%MaxSize; //注意,队列中无论队首还是队尾指针都是正向挪动(顺时针)
//Q.state = 1; //针对记录状态位的情况
//Q.size--; //针对记录长度的情况
return true;
}获取队首元素:
bool GetHead(SqQueue Q, ElemType &x)
{
if(QueueEmpty(Q)) return false;
x = Q.data[Q.front];
return true;
}2.链式队列
主要分为带头结点和不带头结点的,主要区别在于初始化、入队、出队和获取首部元素中,除非内存不足,一般不会出现队满情况。
初始化:
typedef struct LinkNode{ //节点的结构体
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{ //队列结构体
LinkNode *front, *rear;
}LinkQueue;
//初始化————带头结点
void InitQueue(LinkQueue &Q)
{
Q.front = Q.rear = (LinkNode *)malloc(sizeof(LinkNode));
Q.front->next = NULL;
}
//初始化————不带头结点
void InitQueue(LinkQueue &Q)
{
Q.front = NULL;
Q.rear = NULL;
}
//判空————带头结点
bool QueueEmpty(LinkQueue Q)
{
return (Q.front == Q.rear) ? true : false;
}
//判空————不带头结点
bool QueueEmpty(LinkQueue Q)
{
return (Q.front == NULL) ? true : false;
}入队:
//带头结点
void EnQueue(LinkQueue &Q, ElemType x)
{
LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
Q.rear->next = s;
Q.rear = s;
}
//不带头结点————需要对节点进行判断
void EnQueue(LinkQueue &Q, ElemType x)
{
LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
if(Q.front == NULL)
{
Q.front = s;
Q.rear = s;
}
else
{
Q.rear->next = s;
Q.rear = s;
}
}出队:
//带头结点
bool DeQueue(LinkQueue &Q, ElemType &x)
{
if(Q.front == Q.rear) return false;
LinkNode *p = Q.front->next;
x = p->data;
Q.front->next = p->next;
if(Q.rear == p)
Q.rear = Q.front;
free(p);
return true;
}
//不带头结点
bool DeQueue(LinkQueue &Q, ElemType &x)
{
if(Q.front == NULL) return false;
LinkNode *p = Q.front;
x = p->data;
Q.front = p->next;
if(Q.rear == p)
{
Q.front = NULL;
Q.rear = NULL;
}
free(p);
return true;
}3.双端队列
对队列操作有新的约束,允许从两端插入、两端删除,根据题意有不同情况,如允许一端输入两端删除(输入受限的双端队列)、允许两端输入一端删除(输出受限的双端队列)、允许两端输入两端删除等(双端队列)。
考点:判断输出序列合法性。
三、栈和队列的应用
1.栈——括号匹配
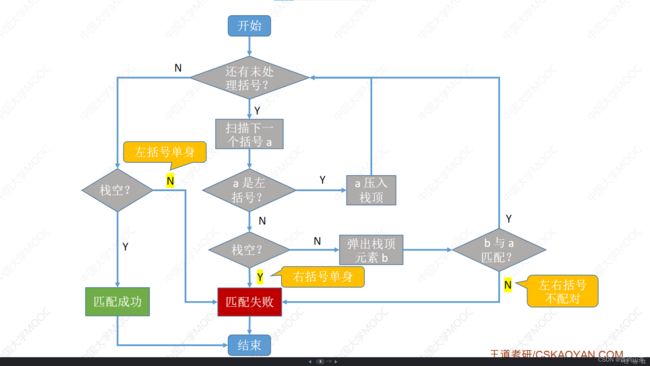
根据数学我们可以发现在一个表达式中最后出现的左括号会最先被匹配,符合栈的LIFO特点,因此遇到左括号就进行入栈操作,遇到右括号就进行出栈操作,使所有括号两两配对。
这是王道总结的整个程序流程图,我觉得很对(配合点头)。
代码实现:
bool bracketCheck(char str[], int length)
{
SqStack S;
InitStack(S);
for(int i=0; i
2.栈——表达式求值
该内容重点在于前缀表达式(波兰表达式)、中缀表达式和后缀表达式(逆波兰表达式)的转换和求值。
根据数学运算式可知,一个算式包括操作数、运算符和界限符(反应计算先后顺序)如((15/(7-(1+1)))*3)-(2+(1+1)),而对于这种算式可以有不同的表达方式,分别为将运算符放在两个操作数之间(中缀)、将运算符放在两个操作数前面(前缀)、将运算符放在两个操作数后面(后缀)。
例:中缀表达式(日常生活用法)a+b-c*d
=> 前缀表达式:-+ab*cd
=> 后缀表达式:ab+cd*-
计算方法(计算机算法,毕竟咱人不搞这些奇怪运算):
1.后缀计算方法:i 从左向右扫描元素,直到处理完全部元素; ii 扫到操作数则入栈,返回 i 继续扫描(注意先出栈的是右操作数); iii 扫到运算符,弹出栈顶两个元素做对应运算,结果压入栈顶,回到 i 继续扫描到全部结束,将结果弹栈赋给记录的变量。
2.前缀计算方法:i 从左向右扫描元素,直到处理完全部元素; ii 扫到操作数则入栈,返回 i 继续扫描(注意先出栈的是左操作数); iii 扫到运算符,弹出栈顶两个元素做对应运算,结果压入栈顶,回到 i 继续扫描到全部结束,将结果弹栈赋给记录的变量。
转换关系(理论,不涉及代码):
1.中缀转后缀:i 确定算式中每个运算符运算顺序; ii 选择下一个运算符,按照 [左操作数 右操作数 运算符] 的形式进行改写(一般遵循左优先原则,即先转换最左侧可转换的算式,保证运算顺序唯一性,计算机看了都说好); iii 重复直到全部转换完毕。
2.中缀转前缀:i 确定算式中每个运算符运算顺序; ii 选择下一个运算符,按照[运算符 左操作数 右操作数] 的形式进行改写(一般遵循右优先原则,即先转换最右侧可转换的算式); iii 重复直到全部转换完毕。
计算机计算方法:
1.中缀转后缀:初始化一个栈(运算符栈),用于保存暂时还不能确定运算顺序的运算符,从左到右依次处理各个数据元素,直到末尾:
i 遇到操作符,直接加入后缀表达式;
ii 遇到界限符(括号)左括号入栈,右括号依次弹栈加入表达式,直到弹出匹配的左括号;
iii 遇到运算符,依次弹出栈内优先级高于或等于当前运算符的所有运算符,并加入表达式,若遇到‘(’或栈空停止,压入当前运算符。
重复直到处理完全部内容,将栈中剩余运算符依次弹出,加入表达式。
2.中缀表达式计算:初始化两个栈——操作数栈和运算符栈,扫描到操作数压入操作数栈,扫描到运算符或界限符,按照”中缀转后缀“相同逻辑压入运算符(期间涉及弹出运算符时,遵循每弹出一个运算符对应弹出两个操作数的原则,并将运算结果压回操作数栈)== 中缀转后缀+后缀表达式计算。
3.后缀表达式计算:i 从左向右依次扫描,直到处理完全部元素; ii 扫描到操作数则入栈(操作数栈),并返回 i ; iii 若扫描的到运算符则弹出两个栈顶元素(先出栈是右操作数),执行相应运算,并将运算结果压栈。
以下是本内容的知识整理,王道就是牛哇!!
3.栈——递归
函数调用时需要一个栈存储:i 调用返回地址; ii 实参; iii 局部变量(即记录函数调用顺序和函数相关数据)
递归算法可将原始问题转变为属性相同但规模较小的问题,但太多层的递归会造成栈溢出,效率也相对较低。
4.队列应用
包括树的层次遍历、图的广度优先遍历(BFS),操作系统线程处理(FCFS)
四、数组和特殊矩阵
1.常用数组
计算机内部主要包括一维数组和二维数组(本质是一维数组组成的数组),一维数组 a[i] 存放的地址 = LOC + i * sizeof(ElemType) 这是下标从0开始的情况,注意审题;二维数组 b[i][j] 存放的地址 = LOC + (i * N + j) * sizeof(ElemType) N为初始行长度(行优先存储法,列优先同理让 j*M+i,M为初始列长)
2.特殊矩阵
1.对称矩阵的压缩存储
只存储主对角线+下三角区(或上三角区),按行优先原则将元素放入一维数组中,实现空间从n*n到(1+n)*n/2的转变,地址从矩阵下标映射为一维数组下标,其中aij ->B[k] 时,aij是B数组中下标 k = i(i - 1) / 2 + j - 1 (注意矩阵从a11存储,B[k]从B[0]开始,因此会有-1操作)
2.三角矩阵的压缩存储
下(上)三角矩阵:除了对角线和下(上)三角区,其他元素都相同(与线性代数中三角矩阵不同,其他地方是有元素的,只不过是相同的元素),按行优先将不同元素存入一维数组,在最后一个位置存放相关元素c。
3.三对角矩阵的压缩存储
又称带状矩阵,当| i - j |>1时aij = 0,压缩存储时按行优先原则只存储带状部分,aij是B数组中下标k = 2i + j -3个元素(下标从0开始)
已知下标k求aij方法:
4.稀疏矩阵的压缩存储
i 三元组顺序存储<行,列,值>
ii 十字链表法(有点意思)
以下是该部分的总结,感谢王道霸霸~
五、课后习题
每天两道有益身心健康,一会下课回来写呜呜