图论-最短路-单源最短路-Dijkstra(堆优化版)

众所周知, 最短路是图论中非常常见的算法,而Dijkstra又作为常用的算法深受青睐
笔者希望通过该文让刚入门图论的新人能够对于迪杰斯特拉算法能有一个较为完整的认识

Let’s Start!

什么叫做最短路?

这是求出一个点到另一个点之间的最短距离,有些时候可以用DFS(搜索)来解决,但是针对一些特殊情况,比如没有方向或者有负权边的时候,用搜索就会很容易超时或者根本无法解决问题,因为搜索必须有明确的方向.

借用一段正规的定义

在一个无权的图中，若从一个顶点到另一个顶点存在着一条路径，则称该路径长度为该路径上所经过的边的数目，它等于该路径上的顶点数减1。由于从一个顶点到另一个顶点可能存在着多条路径，每条路径上所经过的边数可能不同，即路径长度不同，把路径长度最短（即经过的边数最少）的那条路径叫作最短路径或者最短距离。
对于带权的图，考虑路径上各边的权值，则通常把一条路径上所经边的权值之和定义为该路径的路径长度或带权路径长度。从源点到终点可能不止一条路径，把带权路径长度最短的那条路径称为最短路径，其路径长度（权值之和）称为最短路径长度或最短距离。

在正式开始题目之前,请保证已经能够理解邻接表的使用
如果没有,可以先学习或者
看这篇博文
好,那就让我们进入第一道题
Dijkstra求最短路 Ⅰ–AcWing

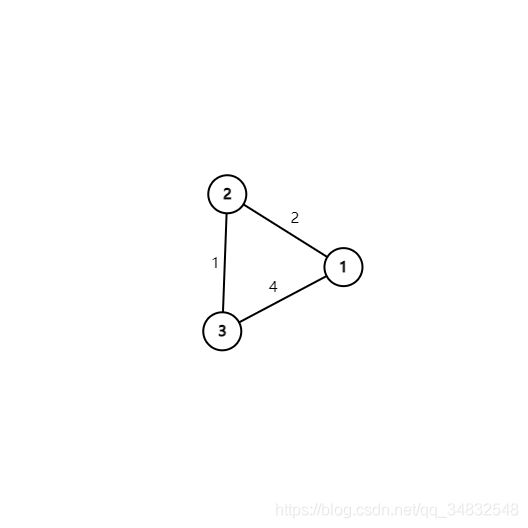
给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入样例

3 3
1 2 2
2 3 1
1 3 4

输出样例

3

看到这个样例,也许你会觉得就这?
有手的都知道肯定是三啊

但如果我给你的是这个图,你又能否在第一时间看出正确答案呢?
是不是没有那么轻松呢

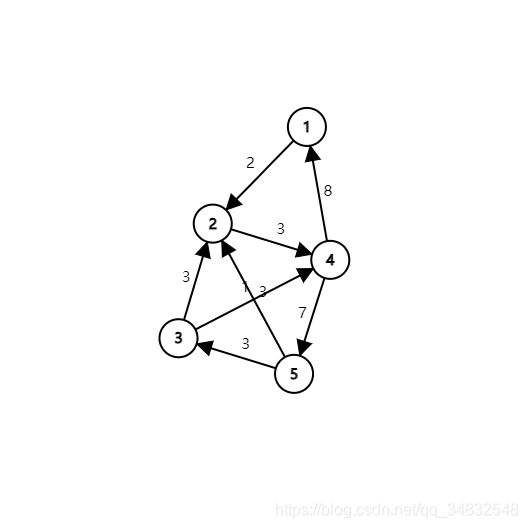
既然如此,那就进入我们的正题,即迪杰斯特拉算法到底是依靠什么来实现的
首先,我们需要一个数组dis,并用memset把它定义为0x3f(非常大)

int dis[100010];
memset(dis,0x3f,sizeof dis);

这个数组有什么用呢?
他是为了确定点1到点n(本文中所有的n均为点的个数)
之间是否存在一条通路,如果不存在那么

dis[n]=0x3f3f3f3f;

同理如果存在,那么所得到的是就是最短路径,其实不光光是n点,1-n之间任意一个点的最短路径都被储存在了数组里,神奇吧 =W=
这其实是一种最短路径树,那到底是如何实现的呢,让我们继续分析
为了方便后面的学习,我们直接使用堆优化过的迪杰斯特拉算法,采用这种优化的好处是
能够大大减小复杂度,能在很大程度上避免被TLE,当然如果出题人故意恶心你卡你那就没只能采取别的办法,当然会在后续专题中继续解决
如上所述,我们先建立一个递增堆并借用pair函数的帮助,你可能会问,为什么要用到pair,其实是因为我们希望输入进堆的包括当前节点pos以及前面已知的最短距离diss

#include 
using namespace std;
typedef pair<int,int>PII;
priority_queue<PII,vector<PII>,greater<PII> >heap;
int diss1=heap.top().diss;
int pos1=heap.top().pos;

也许你也想用结构体表示
满足你!但是请先跟着学完再看

#include 
struct node {
	int diss,pos;
};
bool operator<(node x1,node x2) {
	return x1.diss>x2.diss;
}
priority<node> heap;
	int diss1=heap.top().diss;
	int pos1=heap.top().pos;

接着,我们就从堆的最小值开始取,细心的你一定发现,我们是以到第一个点的距离为关系来排序的
先输入起点,即距离为0,当前点为一进行操作,直到堆中再也没有一个元素,就表明我们已经进行了所有判定,跳出结束

	heap.push({0,1});
		while(heap.size()) {
		PII t=heap.top();
		int diss=t.first;
		int pos=t.second;
		heap.pop();//记住一定要跳出!
	}

同理给出结构体版本

	node temp;
	temp.diss=0;
	temp.pos=1;
	heap.push(temp);
	while(heap.size()) {
		int diss1=heap.top().diss;
		int pos1=heap.top().pos;
		heap.pop();	//记住一定要跳出!
	}

好了,头开起来了,但是我们还是不知道如何判定,不急,听我慢慢分析
首先,我们一直是按着最短路径求的,那么有可能有有一个点重复判定,意思就是说可能在我们判定到这个点pos的是否,会有不同diss,那么我们该如何取舍呢?
没错,最短路,那我们就只要最短的那个,另外一个我们不能要,这时我们就需要一个vis数组来纪录在整个算法运行的时是否出现判定过该点,如果判定过按照大根堆的排序那么这个点的diss,也就是到第一个点的距离必然大于上一个出现该点pos的距离,那我们就大气地不要

int vis[10010]//定义为全局变量后vis数组内每个数都是0
while(......)
{
....
if(vis[pos])
continue;
vis[pos]=1;
}

好了,那么假如这个点是第一次出现,那么下一步该怎么做?
既然你已经知道了邻接表的用法,那么首先这个你一定不陌生

void add(int u,int v,int t) {
	to[cnt]=v;
	val[cnt]=t;
	nex[cnt]=head[u];
	head[u]=cnt++;
}

找到该结点的下一个数to[cnt]=v;
收集该点的值val[cnt]=t;

假设我们已经得到了该点pos和diss
那么从该点一直到这条路上的最后一个点我们进行遍历

  for(int i=head[pos];i!=-1;i=nex[i])

并且定义j表示为该点的下一个节点
如果到已经记录的下一个节点j的距离大于当前到j的距离

 if(dis[j]>val[i]+diss)

那么我们就把他修改成该最短距离,并且把这个点输入进堆继续判定
表明我们已经确定了前j个数的最短路径,并进行第j个数的判断
此时如果j点还未有判定过,那么就判断j点,否则便会跳过

dis[j]=val[i]+diss;
heap.push({dis[j],j});

好啦,是不是晕头转向的,别急,先把最后的收尾工作做了

	memset(dis,0x3f,sizeof dis);
	memset(head,-1,sizeof head);
	cin>>n>>m;
	while(m--) {
		cin>>x>>y>>z;
		add(x,y,z);
	}
	Dijkstra();
	if(dis[n]==0x3f3f3f3f) {
		cout<<"-1";
		return 0;
	}
	cout<<dis[n];

这是我们主函数 要记得先把dis定义为0x3f,以及把head函数定为-1
这样在后面邻接表的判定中如果是-1这表明这条路不存在
或者你也可以省去这一步,不过在add函数中就要多加一条
戳我

void add(int u,int v,int t) {
	cnt++;
	to[cnt]=v;
	val[cnt]=t;
	nex[cnt]=head[u];
	head[u]=cnt;
}

for(int i=head[pos];i;i=nex[i])

AC代码

#include 
#include 
#include 
#include 
using namespace std;
typedef pair<int,int> PII;
int n,m,x,y,z;
const int N=100010;
int to[N],val[N],head[N],cnt,dis[N],idx,nex[N],vis[N];
void add(int u,int v,int t) {
	to[cnt]=v;
	val[cnt]=t;
	nex[cnt]=head[u];
	head[u]=cnt++;
}
void Dijkstra() {
   priority_queue<PII,vector<PII>,greater<PII> >heap;
	dis[1]=0;
	heap.push({0,1});
	while(heap.size()) {
		PII t=heap.top();
		int diss=t.first;
		int pos=t.second;
		heap.pop();
		if(vis[pos])
			continue;
		vis[pos]=1;
        for(int i=head[pos];i!=-1;i=nex[i])
        {
            int j=to[i];
            if(dis[j]>val[i]+diss)
            {dis[j]=val[i]+diss;
            heap.push({dis[j],j});
            }
        }
	}
}
int main() {
	memset(dis,0x3f,sizeof dis);
	memset(head,-1,sizeof head);
	cin>>n>>m;
	while(m--) {
		cin>>x>>y>>z;
		add(x,y,z);
	}
	Dijkstra();
	if(dis[n]==0x3f3f3f3f) {
		cout<<"-1";
		return 0;
	}
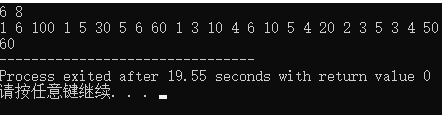
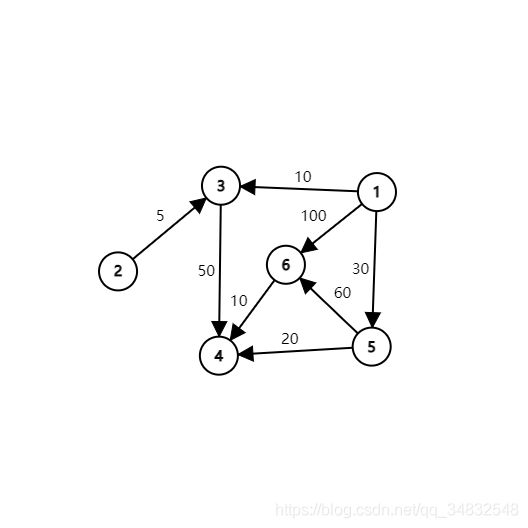
	cout<<dis[n];
}

诶诶诶,没完呢,让我们再来推导一下这个数据
6 8
1 5 30
1 6 100
5 6 60
5 4 20
4 6 10
2 3 5
3 4 50
1 3 10
和开始的一样,我们先将
0,1输入
从3开始

dis[3]>val[8]+0;

然后到5,6同理
之后结束第一次循环,来到第二次
此时到了第三个点,那么距离diss也就是10此时对第四个点进行尝试,得到数据后跳出循环
之后来到了第六个点,因为自己就是最后的点所以啥也没有跳出啦~
所以接着来到五号点,五号点想找四号点和6号点得到数据跳出循环
接着就来到4号点,4号对6号有边所以进行判定
最后得出答案60,是经过1-5-4-6得到的答案!!