AI Deep Reinforcement Learning Autonomous Driving（深度强化学习自动驾驶）

背景介绍

自动驾驶技术的兴起：自动驾驶技术旨在将车辆的驾驶功能部分或完全交给计算机系统，以提高道路安全性、减少交通拥堵，并提供更多的便利性。这需要车辆能够根据环境和情境做出智能的决策，遵循交通规则并与其他车辆和行人进行协同。

深度学习的崛起：深度学习是一种机器学习技术，它使用神经网络模型来学习数据的抽象特征表示。这些模型具有多层神经元，可以自动从大量数据中提取特征，因此被广泛用于图像、语音、自然语言处理等领域。

强化学习的应用：强化学习是一种让智能体通过与环境交互来学习最优策略的方法。在自动驾驶中，车辆可以被视为智能体，道路和交通环境则为其环境。强化学习能够使车辆从试错中学习，逐步优化驾驶策略。

深度强化学习的结合：深度强化学习将深度学习和强化学习相结合，使用深度神经网络来近似智能体的策略或值函数。这使得自动驾驶车辆能够从大量的传感器数据中提取信息，并根据车辆的状态和环境来做出决策，比如加速、减速、转向等。

挑战与机遇：尽管深度强化学习在自动驾驶领域取得了显著进展，但仍然面临着许多挑战。其中包括安全性、决策的解释性、数据效率等问题。然而，借助深度强化学习，自动驾驶系统能够逐渐提升其决策能力和安全性，为未来的智能交通做出贡献。

鉴于自动驾驶可能从根本上改变机动性和交通运输方式，因此自动驾驶技术已经引起了研究界和企业的高度重视。目前，大部分方法都集中在使用带注释的3D几何地图来定义驾驶行为的形式逻辑上。然而，这种方法的扩展性可能存在问题，因为它严重依赖于外部映射基础设施，而不是主要基于对本地场景的理解。为了实现真正无处不在的自动驾驶技术，业界正在提倡驱动机器人系统的处理能力和导航，这种导航方式不依赖于地图和明确的规则，就像人类在全面理解当前环境后，能够简单地进行更高层次的方向控制（例如，遵循道路路径指令）。最近在这个领域的研究表明，在模拟真实道路情境中，利用GPS进行粗定位和激光雷达对本地场景的理解是可行的。近年来，强化学习（Reinforcement Learning，简称RL）作为机器学习领域的重要分支，专注于解决马尔科夫决策问题（Markov Decision Process，简称MDP）。这种方法使代理能够在与环境互动的过程中选择行动，以最大化某种奖励函数。在模拟环境中，例如电脑游戏，以及机器人操作中的简单任务，强化学习显示出巨大的潜力，有望取得类似超人级别的成就，类似于游戏或国际象棋等情境中。

我们觉得强化学习的通用性使其成为自动驾驶的一个有价值的框架。最为重要的是，它提供了一种纠正机制，以改进自动驾驶在学习后的行为表现。然而，强化学习作为一种专注于解决复杂问题的通用智能方法，在处理时序问题方面具有优势。而自动驾驶作为典型的"工业人工智能"领域，涉及感知、决策和控制这三大环节，必须考虑各种极端工况和场景。在其中，感知过程中环境要素异常复杂，而驾驶任务则多变且灵活，很多情况并非时序问题。因此，仅依靠强化学习来解决这些问题可能相当具有挑战性。在这方面，深度学习（Deep Learning，简称DL）扮演了重要角色，例如常见的YOLO及其衍生版本等。强调的是，对于自动驾驶来说，仅有在决策层面，模型驱动的强化学习（Model Based RL）与基于值的强化学习（Value Based RL）相互协同，基于规则的构建被用来处理大多数常见驾驶场景，但需要不断地进行设计与更新；强化学习则用来解决那些规则库无法涵盖的极端场景和问题。对于一些专注于解决方案的科技公司而言，更倾向于选择深度强化学习（Deep Reinforcement Learning，简称DRL）方法。这种方法将深度学习的感知能力与强化学习的决策能力相结合，使其能够直接根据输入信息进行控制。这种方法更贴近人类的思维方式，也是更具成熟解决方案潜力的体现。

研究背景

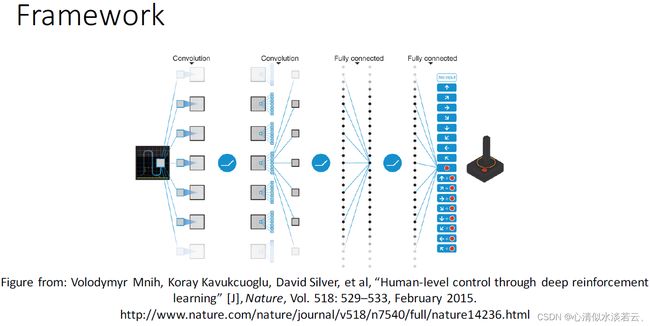
在2015年，DeepMind团队提出了深度Q网络（Deep Q-network，简称DQN）。DQN以一种全新的方式进行学习，它仅使用原始游戏图像作为输入，摒弃了对人工特征的依赖，实现了端到端的学习方法。DQN在创新性地将深度卷积神经网络与Q-learning相融合的基础上，在Atari视频游戏中取得了与人类玩家相媲美的控制效果。通过应用经验回放技术以及引入固定目标Q网络，DQN成功地解决了使用神经网络进行非线性动作值函数逼近时可能出现的不稳定和发散问题，极大地增强了强化学习的适用性。

经验回放技术不仅提高了历史数据的有效利用率，同时通过随机采样打破了数据之间的相关性。固定目标Q网络的引入进一步稳定了动作值函数的训练过程。此外，通过截断奖赏信号并对网络参数进行正则化，DQN限制了梯度的范围，从而实现了更为鲁棒的训练过程。下方展示了DQN网络的结构图：

在2016年的Ben Lua项目中，演示了如何运用深度确定性政策梯度算法（DDPG，Deep Deterministic Policy Gradient）——这是由DeepMind的Lillicrap等人在2016年提出的方法。该方法核心思想在于将卷积神经网络作为策略函数μ和Q函数的近似模型，即策略网络和Q网络。通过深度学习技术对这些神经网络进行训练。

他们将这一方法与Keras框架结合，应用于TORCS（The Open Racing Car Simulator，开放赛车模拟器），这是一个富有趣味性的AI赛车游戏和研究平台。当时，TORCS被视为出色的驾驶仿真平台，因为借助这个仿真环境，我们可以观察神经网络随着时间推移如何进行学习，并检验其学习过程。通过在这一仿真环境中进行实验，我们可以更轻松地理解自动驾驶中的机器学习技术。

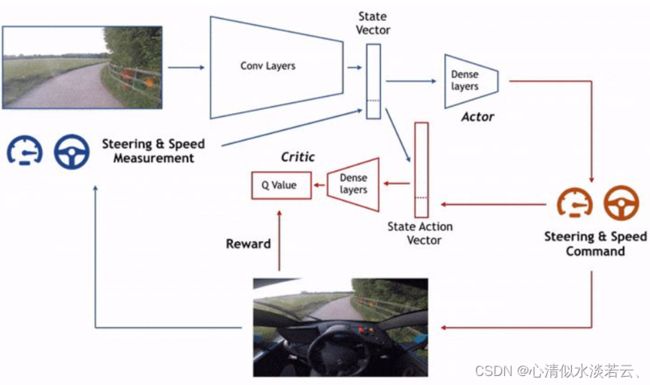
英国自动驾驶初创公司Wayve在2018年公布了其使用Actor-Critic强化学习框架快速训练驾驶策略的论文 。从随机初始化的参数中，他们的模型能够在少量使用单目图像作为输入的训练片段中学习车道跟踪策略，采用的自动驾驶框架，摆脱了对定义的逻辑规则、映射和直接监督的依赖。

研究目的及意义

真正的自动驾驶汽车（即能够在任何要求的环境中安全驾驶）的关键是更加重视关于其软件的自学能力。换句话说，自动驾驶汽车首先是人工智能问题，需要一个非常具体的机器学习开发技能。而强化学习是机器学习的一个重要分支，是多学科多领域交叉的一个产物，它的本质是解决决策（decision making）问题，即自动进行决策，并且可以做连续决策。通过搭建仿真环境，设计强化学习框架，并且无需 3D 地图，也无需规则编程，让汽车从零开始在短时间内学会在模拟真实驾驶环境中自动驾驶。

•  仿真驾驶环境的个性化搭建/复杂环境对代理算法的挑战研究：讨论如何设置系统，以便在现实世界的车辆上高效、安全地学习驾驶；
•  新环境中，为了快速探索全图的策略讨论研究，如数据增强方面：通过连续深度强化学习算法，仅使用车载计算，在几个短视频中学习驾驶一辆模拟真实世界的自动驾驶汽车；
•  强化学习算法框架研究，根据不同环境观测维度精确设计底层框架和损失函数以及奖励机制：算法基于model- based VS model-
  free的有效性对比。

项目设计内容

算法介绍

马尔可夫链及马尔可夫决策过程

马尔可夫链（Markov Chain）：

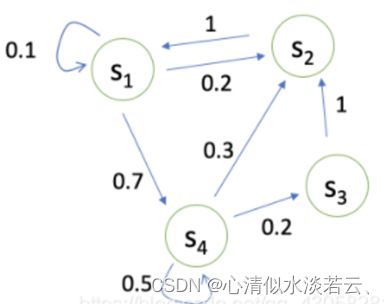
描述状态转移可以用状态转移矩阵：

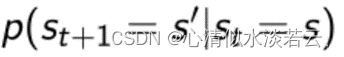
表示agent在st这个状态下的时候到下一个状态的概率：

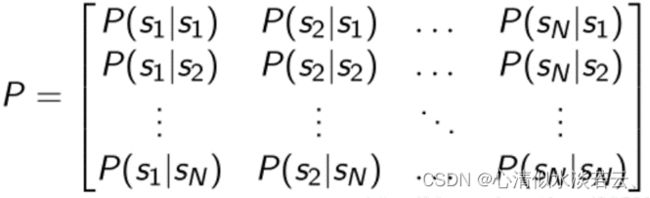
马尔可夫奖励决策过程（Markov Decision Reward Process, MDRP）：MDRP = Markov Chain + reward

与马尔科夫链相比，多了一个奖励函数：

到达某个状态后，可以获得的奖励，其奖励的折扣因子, 折扣因子越大，Agent越关注未来的奖励，而不仅仅只关注当前的利益：

最终的奖励为：

强化学习

强化学习的目标是学习到策略，使得累计回报的期望值最大，即：

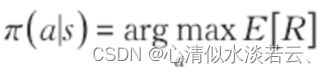
为了便于求解最优策略，引入值函数和动作状态值函数来评价某个状态和动作的优劣。值函数的定义如下：

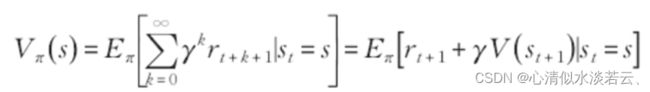
动作状态值函数定义为：

解决值函数和动作状态值函数的方法可以分为基于表的方法和基于值函数逼近的方法。在基于表的方法中，传统的动态规划、蒙特卡洛和时间差分（Temporal Difference，简称TD）算法都属于这一类，其本质是构建一个Q(s,a)表格，其中行表示状态，列表示动作，通过迭代计算不断更新表中的值。如下图所示，上方的三个环境维度展示了在状态较少时，使用Q表能够容纳这些维度，并且在实际决策时遍历较小的表并不会引起明显的时间延迟。

然而，当环境状态数量庞大时，例如围棋盘面状态或机器人运动状态等，状态的数量变得无法计数，这时基于表的方法就无法应用。因此，基于值函数逼近的方法更适用于这些复杂环境。

在强化学习的众多子算法中，分为两大流派：model-based/off-policy 和 value-based/on-policy , 在我们这次的自动驾驶项目中，我们需要关注的是我们的动作是连续的还是离散问题。

当需要解决的问题是连续动作（如gym的carmountin-v0），则采取基于policy gradient的算法：DDPG,PPO,A3C等。

当需要解决的问题是离散动作（CarMountinCounts-v0）时，则可采取基于value的算法，如 Q-learning, DQN, A3C, PPO等。

Deep Q-Network的一大局限性是输出/动作是离散的，而赛车中的转向等动作是连续的。将DQN应用于连续域的一个明显方法是对动作空间进行简单的离散化。且容易遇到了维数的诅咒问题。例如，如果你将方向盘离散化，从-90度到+90度，每5度，加速度从0km到300km，每5km，你的输出组合将是36个转向状态乘以60个速度状态，等于2160种可能的组合。如果你想让机器人执行一些非常专业的操作，比如需要对动作进行精细控制的脑外科手术，而天真的离散化将无法达到操作所需的精度，那么情况就会变得更糟。

所以，连续问题算法DDPG是不错的选择，具体哪个更适合自己搭建的仿真环境，需要经过实验对比得出有效结论。

神经网络

人工神经网络的架构大致可分为两大类。一类是前馈和递归神经网络（RNN），前馈网络采用单个输入（例如游戏状态的表示），并输出每个可能动作的概率值。另一类是卷积神经网络（CNN），它由可训练的滤波器组成，适用于处理图像数据，例如来自视频游戏屏幕的像素。

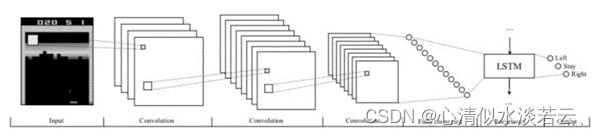
RNN 通常应用于时间序列数据，其中网络的输出取决于先前时间步骤的激活。除了网络的先前隐藏状态与下一个输入一起反馈给网络外，RNN 的训练过程类似于前馈网络。这就允许网络通过记忆先前的激活而变得具有上下文感知，这在那种单个观察不代表完整状态的游戏中是非常有用的。对于视频游戏，通常使用一堆卷积层，然后是循环层和完全连接的前馈层。

仿真平台

OpenAI gym

gym是一个开发和比较强化学习算法的工具包。它对代理的结构没有任何假设，并且与任何数值计算库兼容，比如TensorFlow或Theano。gym的库是一个测试问题的集合环境，你可以用它来解决你的强化学习算法。这些环境有一个共享的接口，允许编写通用算法。
当python>=3.5时，可直接pip install gym
其驾驶环境有：MountainCarContinuous-v0(附上环境配置教程 )，MountainCar-v0 （附python code）

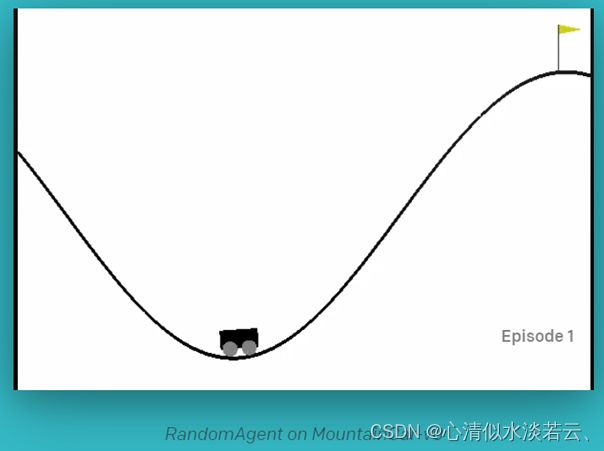
Torcs配置

可以在TORCS中开发自己的智能车，TORCS提供了几种可用的模式，但客户端-服务器模式仅支持两种模型：Practice和Quick Race。其中Practice支持一辆车参加比赛，Quick Race支持多辆车参加比赛。TORCS是一个具有高度可移植性的赛车模拟器。它可作为普通的赛车游戏，同样能做为赛车游戏和人工智能的研究平台。它可运行在Linux(x86，AMD64，PPC)，FreeBSD，Mac OS X和Windows之上。仿真功能包含简单的损伤模型，碰撞，轮胎和车轮属性（弹簧，减震器，刚度等),空气动力学（地面效应，破坏等）及更多。

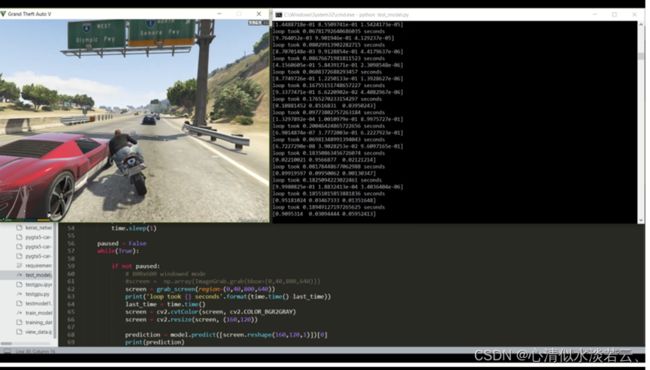
GTA5

Grand Theft Auto是由Rockstar Games开发的以犯罪为主题的世界著名游戏，其中驾驶模拟器被很多强化学习爱好者所使用。

参数选择

行动空间

有人或许会认为驾驶本身囊括了一系列天然的动作，如加速、刹车、信号等。然而，强化学习算法应该在什么领域输出呢？以节流阀为例，它可以被描述为离散的状态，要么是开要么是关，或者在某个范围内如[0,1]的连续度量。另一种选择是重新参数化节流阀的速度设定点，使其与经典控制器中设定点的输出相匹配。总体而言，在一个简单的模拟器环境中，连续动作尽管可能更具挑战性，却提供了更加平滑的控制方式。这种情况下，可以采用二维行动空间，其中包括范围在[-1, 1]内的转向角度以及以km/h为单位的速度设定值。

如图为观测空间，从应用问题来看，越复杂的问题，其观测空间维度越高。

奖励函数

奖励函数的设计可以接近监督学习给定的车道分类系统，奖励学习车道跟踪可以建立在最小化预测距离车道中心，先前的研究 采用的方法。这种方法在规模上是有限的:系统只能与手工制作的奖励背后的人类直觉一样好。我们不采用这种方法。相反，我们将奖励定义为前进速度并在违反交通规则时终止一段情节，因此给定状态V(st)的值对应于在违反交通规则前行驶的平均距离。一个可以识别的错误是代理可能会选择避免更困难的操作，例如在英国向右转(在美国向左)。命令条件奖励可以在未来的工作中使用，以避免这种情况。

环境及软件包

Python软件及依赖包
Python=3.6-3.8
Opencv
Tensorflow-gpu
Keras
Numpy
OpenAI gym

步骤

1.  根据系统配置python软件和环境：推荐miniconda3 + pycharm
2.  配置openAI gym 和深度学习（tensorflow+keras or torch）虚拟环境
3.  驾驶平台搭建和环境设置
4.  强化学习框架设计,奖励函数设计
5.  驾驶渲染记录数据供强化学习训练
6.  训练及验证结论
7.  论文写作

可参考项目

OpenAI gym: https://github.com/andywu0913/OpenAI-GYM-CarRacing-DQN
Torcs平台：https://github.com/yanpanlau/DDPG-Keras-Torcs
GTA平台：https://github.com/Sentdex/pygta5

参考

https://deepmind.com/research/publications/human-level-control-through-deep-reinforcement-learning
https://yanpanlau.github.io/2016/10/11/Torcs-Keras.html Kendall, A. , et al. “Learning to Drive in a Day.” (2018)
https://gym.openai.com/envs/MountainCar-v0
https://www.jianshu.com/p/915671bf670b?utm_campaign=shakespeare
https://gym.openai.com/envs/MountainCar-v0/
https://zhuanlan.zhihu.com/p/57648478
https://github.com/Sentdex/pygta5

基于openAI gym 的mountincar-v0的强化学习code入门

#!/usr/bin/python
# -*- encoding:utf-8 -*-
# @author: cy
# @time: 2021/7/8 下午3:03
# @project_name: PyCharm
# @file: car.py
'''
import gym
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

# configuration parameters for whole step
seed=42
gamma=0.99 #discount
max_steps_per_episode=10000

# env
env=gym.make('MountainCar-v0')
# env=gym.make('CartPole-v0')
# env.seed(seed)
env.reset()
action = env.action_space.sample()
# print('action',action)
# action = env.action_space
# state = tf.convert_to_tensor(state)
# state = tf.expand_dims(state, 0)
for i in range (1000):
    # action = np.random.choice(2, p=np.squeeze(1))
    env.render()
    # action = np.random.uniform(action)
    abs,r,done,info=env.step(action)
    # print(abs)
    # print(done)
    # print(info)

env.close()
'''

import numpy as np
import gym
from gym import wrappers

off_policy = True  # if True use off-policy q-learning update, if False, use on-policy SARSA update

n_states = 40  # Discrete value
iter_max = 100
initial_lr = 1.0  # Learning rate
min_lr = 0.003
gamma = 0.99
t_max = 10000
eps = 0.1

'''
observation state :(2,)
'''
def obs_to_state(env, obs):
    """ Maps an observation to state """
    # we quantify the continous state space into discrete space
    env_low = env.observation_space.low  # !
    env_high = env.observation_space.high  # !
    env_dx = (env_high - env_low) / n_states  # state discretization
    a = int((obs[0] - env_low[0]) / env_dx[0])  # '/'
    b = int((obs[1] - env_low[1]) / env_dx[1])
    # print('env_low:{}    env_high:{}   env_dx:{}  obs[0]:{}  obs[1]:{}  a:{}  b:{}'.format(env_low,env_high,env_dx,obs[0],obs[1],a,b))
    '''
    env_low:[-1.2  -0.07]    env_high:[0.6  0.07]   env_dx:[0.045  0.0035]  obs[0]:-0.8533420682038003  obs[1]:-0.03403819682165786  a:7  b:10
    '''
    return a, b


def run_episode(env, policy=None, render=False):
    obs = env.reset()  # reset env
    total_reward = 0
    step_idx = 0
    for _ in range(t_max):  # we know it can end the game in 10000 step
        if render:
            env.render()  # fresh env

        if policy is None:
            action = env.action_space.sample()  # initialize action
        else:  # policy chose , the action is fixed
            a, b = obs_to_state(env, obs)  # it comes from the number34 code
            action = policy[a][b]

        obs, reward, done, _ = env.step(action)
        total_reward += gamma ** step_idx * reward
        step_idx += 1
        if done:
            break
    return total_reward


if __name__ == '__main__':
    env_name = 'MountainCar-v0'  # the name of id can search
    env = gym.make(env_name)  # make a env
    env.seed(0)  # let the resule can be same
    np.random.seed(0)  # let the resule can be same
    if off_policy == True:  # confirm the policy
        print('----- using Q Learning -----')
    else:
        print('------ using SARSA Learning ---')

    q_table = np.zeros((n_states, n_states, 3))  # 3 action，and the dimensional of state is 3

    for i in range(iter_max):  # the ep is 5000
        obs = env.reset()  # reset the env
        total_reward = 0  # 0 reward

        ## eta: learning rate is decreased at each step
        eta = max(min_lr, initial_lr * (0.85 ** (i // 100)))
        for j in range(t_max):  # the ep is 10000,after we need reset env
            a, b = obs_to_state(env, obs)  # State value after discretization
            if np.random.uniform(0, 1) < eps:
                action = np.random.choice(env.action_space.n)  # such as 0,1,2
            else:
                action = np.argmax(q_table[a][b])

            obs, reward, done, _ = env.step(action)
            total_reward += reward

            # update q table
            a_, b_ = obs_to_state(env, obs)
            if off_policy == True:
                # use q-learning update (off-policy learning)
                q_table[a][b][action] = q_table[a][b][action] + eta * (
                            reward + gamma * np.max(q_table[a_][b_]) - q_table[a][b][action])
            else:
                # use SARSA update (on-policy learning)
                # epsilon-greedy policy on Q again
                if np.random.uniform(0, 1) < eps:
                    action_ = np.random.choice(env.action_space.n)
                else:
                    action_ = np.argmax(q_table[a_][b_])
                q_table[a][b][action] = q_table[a][b][action] + eta * (
                            reward + gamma * q_table[a_][b_][action_] - q_table[a][b][action])
            if done:
                break

        if i % 200 == 0:  # print learning info per 200 steps
            print('Iteration #%d -- Total reward = %d.' % (i + 1, total_reward))
    solution_policy = np.argmax(q_table, axis=2)
    solution_policy_scores = [run_episode(env, solution_policy, False) for _ in range(100)]
    print("Average score of solution = ", np.mean(solution_policy_scores))
    # Animate it
    for _ in range(2):
        run_episode(env, solution_policy, True)
    env.close()