2021牛客暑期多校训练营1（部分补题）

2021牛客暑期多校训练营1

A题

博弈，找规律，在A不能取完的基础上，即a[i][j]为0的情况，在两堆分别加一个k和s*k，打个表，注意用bool数组，不然会超时。

#include
#include
#include
#include
using namespace std;

const int N = 5e3 + 10;
bool a[N][N];

int main() {
	//打表
	for (int i = 0; i <= 5000; i++) {
		for (int j = 0; j <= 5000; j++) {
			if (!a[i][j]) {
				for (int k = 1; k + i <= 5000; k++) {
					for (int s = 0; s * k + j <= 5000; s++) {
						a[k + i][s * k + j] = 1;
					}
				}
				for (int k = 1; k + j <= 5000; k++) {
					for (int s = 0; s * k + i <= 5000; s++) {
						a[s * k + i][k + j] = 1;
					}
				}
			}
		}
	}
	int t;
	cin >> t;
	int n, m;
	while (t--) {
		cin >> n >> m;
		if (a[n][m])cout << "Alice" << endl;
		else cout << "Bob" << endl;
	}
	return 0;
}

B题


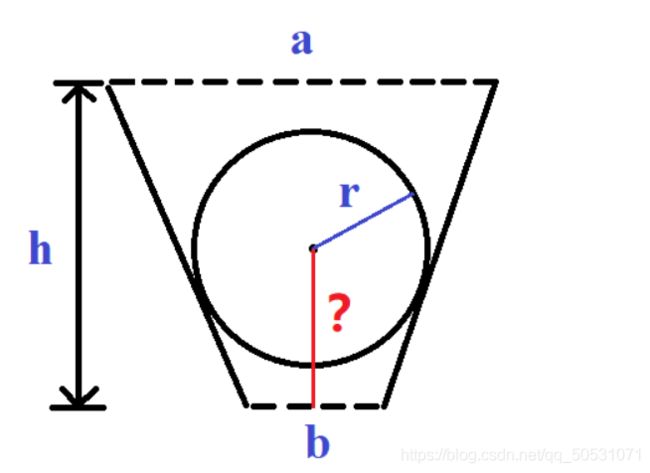
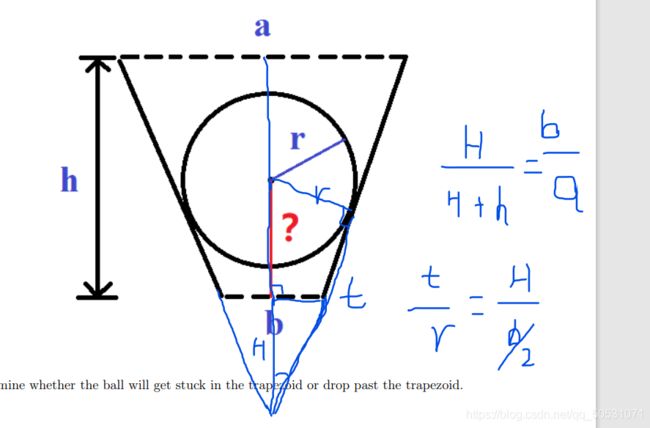
如图二所示，利用三角形相似求出t和H，需要求的值即为t²+r²的根号值减去H。

#include
#include
#include
#include
using namespace std;

const int N = 2e3 + 10;

int main() {
	double r, a, b, h;
	cin >> r >> a >> b >> h;
	
	if (r < b / 2)cout << "Drop" << endl;
	else {
		cout << "Stuck" << endl;
		double H = b * h / (a - b);
		double t = 2 * H * r / b;
		double cnt = pow(pow(t,2) + pow(r,2), 1.0/2.0) - H;
		printf("%.10lf", cnt);
	}
	return 0;
}

D题
因为老师的图片只能横向插入，就看每一行有多少连续的零就行。

#include
#include
#include
using namespace std;

const int N = 5e6 + 10;
char a[N], b[N];

int main() {
	int n, m;
	cin >> n >> m;
	int cnt = 0;
	int ck = 0;
	for (int i = 1; i <= n * n; i++) {
		cin >> a[i];
		if (a[i] == '0')ck++;
		else if (a[i] == '1')ck = 0;
		if (ck >= m)cnt++;
		if (i % n == 0)ck = 0;
	}
	cin >> b;
	cout << cnt << endl;
	return 0;
}

F题
求一个数有任意子串对3取模为0，三位数往上，任意数都有子串对3取模为零，枚举了100以内不符合题意的数，暴力打表，然后判断l,r的大小，记录数据即可。

#include
#include
#include
#include
using namespace std;

const int N = 2e3 + 10;
int a[101];

int main() {
	for (int i = 1; i <= 100; i++) {
		if (i == 1 || i == 2 || i == 4 || i == 5 || i == 7 || i == 8 || i == 11  || i == 14 || i == 17 || i == 22 || i == 25 || i == 28 || i == 41 || i == 44 || i == 47 || i == 52 || i == 55 || i == 58 || i == 71 || i == 74 || i == 77 || i == 82 || i == 85 || i == 88) {
			a[i] = 1;
		}
		//cout << a[i] << endl;
	}
	int t;
	cin >> t;
	while (t--) {
		long long l, r;
		cin >> l >> r;
		long long cnt = 0;
		if (l < 100 && r < 100) {
			for (int i = l; i <= r; i++) {
				if (a[i] == 0)cnt++;
			}

		}
		else if (l < 100 && r >= 100) {
			for (int i = l; i <= 100; i++) {
				if (a[i] == 0)cnt++;
			}
			cnt += r - 100;
		}
		else {
			cnt = r - l + 1;
		}
		cout << cnt << endl;
	}
	return 0;
}

G题
题意，求对ai进行k次交换之后ai与bi之间最大的绝对值差，因为是对绝对值求和，所以也可以对bi进行交换，结果是一样的
要如何交换才能将绝对值变大呢，可以假设我们有四个数字a1,a2,b1,b2，并且a1>b1,a2>b2,
一种情况，当b1>a2时,|a1-b1|+|a2-b2|=a1+a2-b1-b2
进行交换后：|a1-b2|+|a2-b1|=a1-b2+b1-a2=a1+b1-a2-b2
交换后增加的数值：2 * b1 - 2 * a2
另一种情况，b1 对于|a1-b1|+|a2-b2|=a1+a2-b1-b2
交换后：|a1-b2|+|a2-b1|=a1-b2+a2-b1=a1+a2-b1-b2
交换后数值没有增加。
所以对于ai数组和bi数组最多有m次有效交换，只需要判断k，k<=m,进行k次有效交换，k>m,进行m次有效交换，然后跳出循环。
需要对n=2进行特判。

#include
#include
#include