【算法题】螺旋矩阵 I II III IV
目录
1. 螺旋矩阵
2. 螺旋矩阵 II
3. 螺旋矩阵 III
4. 螺旋矩阵 IV
1. 螺旋矩阵
题目描述:
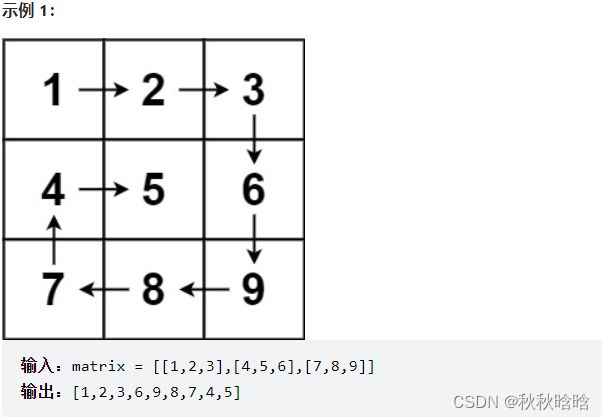
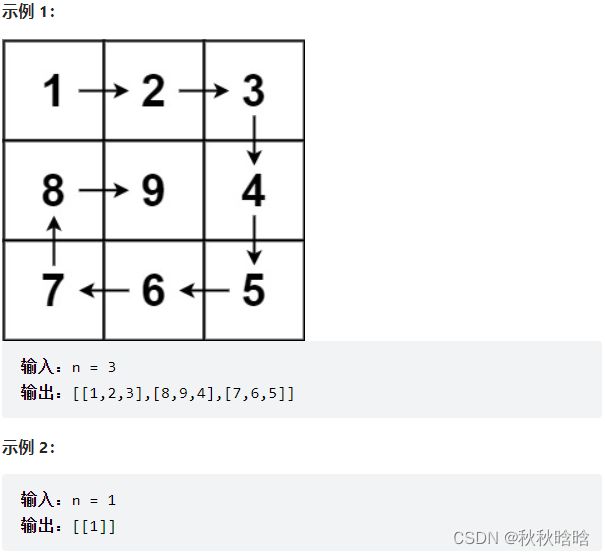
给你一个m行n列的矩阵matrix,请按照顺时针螺旋顺序 ,返回矩阵中的所有元素。
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 10
- -100 <= matrix[i][j] <= 100
题解:
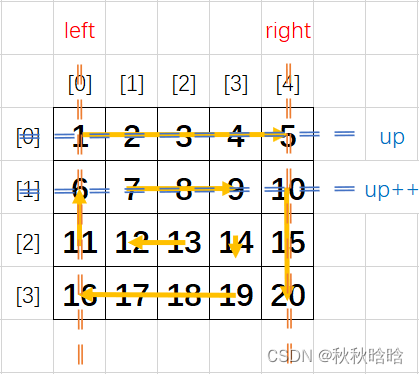
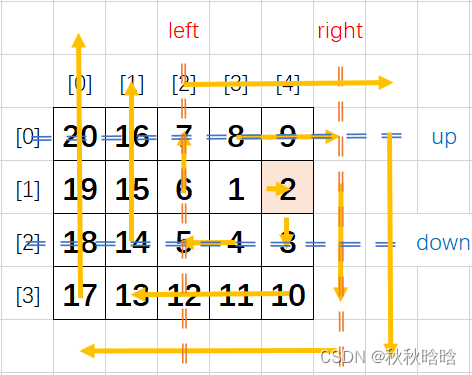
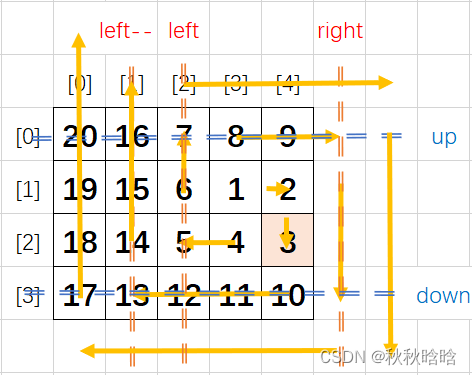
4×5的矩阵按顺时针螺旋顺序打印如图所示。
- 每次从左往右走,都是从left走向right,结束后up++
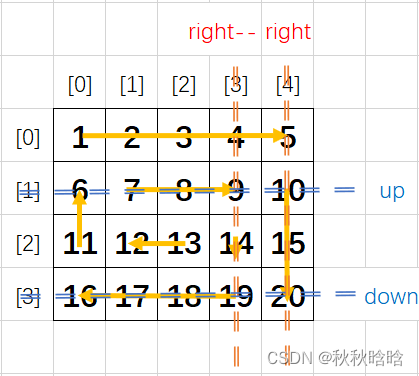
- 每次从上往下走,都是从up走向down,结束后right--
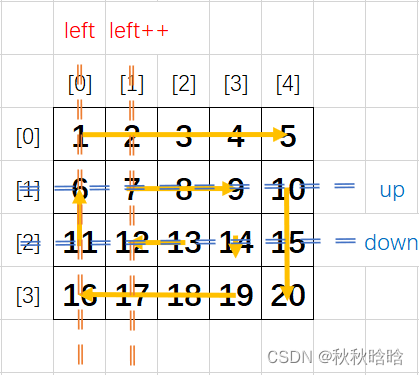
- 每次从右往左走,都是从right走向left,结束后down--
- 每次从下往上走,都是从down走向up,结束后left++
所以,螺旋矩阵每次循环分为4步;左→右、上→下、右→左、下→上,直到up>down或left>right跳出循环。
class Solution {
public:
vector spiralOrder(vector>& matrix) {
vector ans;
int m = matrix.size(); //行
int n = matrix[0].size();//列
int up = 0; //上边界
int down = m - 1; //下边界
int left = 0; //左边界
int right = n - 1;//右边界
while (1)
{
//左→右
for (int j = left; j <= right; j++)
{
ans.push_back(matrix[up][j]);
}
if (++up > down)
{
break;
}
//上→下
for (int i = up; i <= down; i++)
{
ans.push_back(matrix[i][right]);
}
if (--right < left)
{
break;
}
//右→左
for (int j = right; j >= left; j--)
{
ans.push_back(matrix[down][j]);
}
if (--down < up)
{
break;
}
//下→上
for (int i = down; i >= up; i--)
{
ans.push_back(matrix[i][left]);
}
if (++left > right)
{
break;
}
}
return ans;
}
}; 测试:
int main()
{
vector> matrix = { {1,2,3,4,5},{6,7,8,9,10},{11,12,13,14,15},{16,17,18,19,20} };
Solution s;
vector v = s.spiralOrder(matrix);
for (auto e : v)
{
cout << e << " ";
}
cout << endl;
return 0;
} 2. 螺旋矩阵 II
题目描述:
给你一个正整数n,生成一个包含1到n^2所有元素,且元素按顺时针顺序螺旋排列的n x n正方形矩阵matrix。
提示:
- 1 <= n <= 20
题解:
class Solution {
public:
vector> generateMatrix(int n) {
vector> ans(n, vector(n));//n*n的二维数组
int up = 0; //上边界
int down = n - 1; //下边界
int left = 0; //左边界
int right = n - 1;//右边界
int num = 1; //顺时针递增的矩阵元素
while (1)
{
//左→右
for (int j = left; j <= right; j++)
{
ans[up][j] = num++;
}
if (++up > down)
{
break;
}
//上→下
for (int i = up; i <= down; i++)
{
ans[i][right] = num++;
}
if (--right < left)
{
break;
}
//右→左
for (int j = right; j >= left; j--)
{
ans[down][j] = num++;
}
if (--down < up)
{
break;
}
//下→上
for (int i = down; i >= up; i--)
{
ans[i][left] = num++;
}
if (++left > right)
{
break;
}
}
return ans;
}
}; 测试:
int main()
{
Solution s;
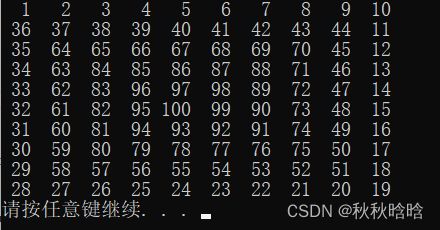
vector> v = s.generateMatrix(10);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("%3d ", v[i][j]);
}
printf("\n");
}
return 0;
} 3. 螺旋矩阵 III
题目描述:
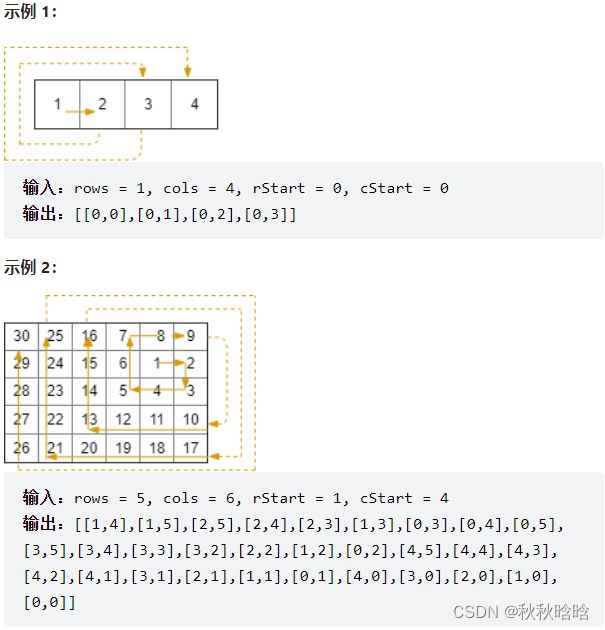
在rows x cols的网格上,你从单元格 (rStart, cStart) 面朝东面开始。网格的西北角位于第一行第一列,网格的东南角位于最后一行最后一列。
你需要以顺时针按螺旋状行走,访问此网格中的每个位置。每当移动到网格的边界之外时,需要继续在网格之外行走(但稍后可能会返回到网格边界)。
最终,我们到过网格的所有rows x cols个空间。
按照访问顺序返回表示网格位置的坐标列表。
提示:
- 1 <= rows, cols <= 100
- 0 <= rStart < rows
- 0 <= cStart < cols
题解:
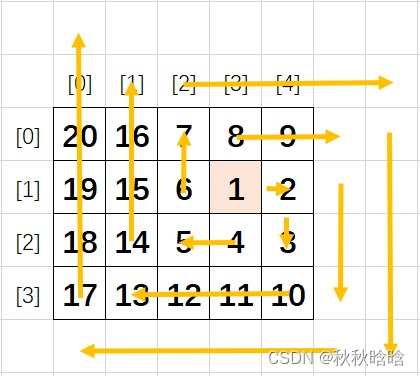
以下图矩阵为例:
假设初始坐标为(rStart, cStart),上边界为rStart-1,下边界为rStart+1,左边界为cStart-1,右边界为Start+1。
假设当前坐标为(x, y)。
- 每次从左往右走,都是从(x, y+1)走向(x, right),结束后right++
- 每次从上往下走,都是从(x+1, y)走向(down, y),结束后down++
- 每次从右往左走,都是从(x, y-1)走向(x, left),结束后left--
- 每次从下往上走,都是从(x-1, y)走向(up, y),结束后up--
重复循环左→右、上→下、右→左、下→上,当答案数组的元素个数==网格面积时,表示已遍历完网格的全部元素。
class Solution {
public:
vector> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {
vector> ans{ { rStart,cStart } };//先把起点存入答案数组
int count = 1;//表示答案数组的元素个数
int up = rStart - 1; //上边界
int down = rStart + 1; //下边界
int left = cStart - 1; //左边界
int right = cStart + 1;//右边界
int x = rStart;//当前位置横坐标
int y = cStart;//当前位置纵坐标
int area = rows * cols;//网格面积,即所有元素的个数
if (area == 1)
{
return ans;
}
while (1)
{
//左→右
for (int j = y + 1; j <= right; j++)
{
//检查坐标是否在网格中
if (x >= 0 && x < rows && j >= 0 && j < cols)
{
ans.push_back({ x,j });
if (++count == area)
{
return ans;
}
}
}
y = right;//更新当前位置纵坐标
right++;
//上→下
for (int i = x + 1; i <= down; i++)
{
//检查坐标是否在网格中
if (i >= 0 && i < rows && y >= 0 && y < cols)
{
ans.push_back({ i,y });
if (++count == area)
{
return ans;
}
}
}
x = down;//更新当前位置横坐标
down++;
//右→左
for (int j = y - 1; j >= left; j--)
{
//检查坐标是否在网格中
if (x >= 0 && x < rows && j >= 0 && j < cols)
{
ans.push_back({ x,j });
if (++count == area)
{
return ans;
}
}
}
y = left;//更新当前位置纵坐标
left--;
//下→上
for (int i = x - 1; i >= up; i--)
{
//检查坐标是否在网格中
if (i >= 0 && i < rows && y >= 0 && y < cols)
{
ans.push_back({ i,y });
if (++count == area)
{
return ans;
}
}
}
x = up;//更新当前位置横坐标
up--;
}
}
}; 测试:
int main()
{
Solution s;
vector> v = s.spiralMatrixIII(4, 5, 1, 3);
for (int i = 0; i < v.size(); i++)
{
for (int j = 0; j < v[0].size(); j++)
{
cout << v[i][j] << " ";
}
cout << endl;
}
return 0;
} 4. 螺旋矩阵 IV
题目描述:
给你两个整数:m和n,表示矩阵的维数。
另给你一个整数链表的头节点head。
请你生成一个大小为m x n的螺旋矩阵,矩阵包含链表中的所有整数。链表中的整数从矩阵左上角开始、顺时针按螺旋顺序填充。如果还存在剩余的空格,则用-1填充。
返回生成的矩阵。
提示:
- 1 <= m, n <= 105
- 1 <= m * n <= 105
- 链表中节点数目在范围[1, m * n] 内
- 0 <= Node.val <= 1000
题解:
class Solution {
public:
vector> spiralMatrix(int m, int n, ListNode* head) {
vector> ans(m, vector(n, -1));//m*n的二维数组,全部初始化为-1
int up = 0; //上边界
int down = m - 1; //下边界
int left = 0; //左边界
int right = n - 1;//右边界
ListNode* cur = head;
while (1)
{
//左→右
for (int j = left; j <= right; j++)
{
if (cur == nullptr)
{
return ans;
}
ans[up][j] = cur->val;
cur = cur->next;
}
if (++up > down)
{
break;
}
//上→下
for (int i = up; i <= down; i++)
{
if (cur == nullptr)
{
return ans;
}
ans[i][right] = cur->val;
cur = cur->next;
}
if (--right < left)
{
break;
}
//右→左
for (int j = right; j >= left; j--)
{
if (cur == nullptr)
{
return ans;
}
ans[down][j] = cur->val;
cur = cur->next;
}
if (--down < up)
{
break;
}
//下→上
for (int i = down; i >= up; i--)
{
if (cur == nullptr)
{
return ans;
}
ans[i][left] = cur->val;
cur = cur->next;
}
if (++left > right)
{
break;
}
}
return ans;
}
}; 测试:
int main()
{
ListNode* preHead = new ListNode;
ListNode* tail = preHead;
for (int i = 3; i <= 15; i++)
{
ListNode* newNode = new ListNode(i);
tail->next = newNode;
tail = tail->next;
}
Solution s;
vector> v = s.spiralMatrix(3, 5, preHead->next);
for (int i = 0; i < v.size(); i++)
{
for (int j = 0; j < v[0].size(); j++)
{
printf("%2d ", v[i][j]);
}
printf("\n");
}
return 0;
}