空间数据库理论基础

空间数据库理论基础

1.空间数据库概述

空间数据分为矢量数据和栅格数据

[1]空间实体

不可再分的最小单元现象称为空间实体

• 对存在于这个自然世界中地理实体的抽象
• 包括点、线、多边形等基本类型

空间实体举例

一根电线杆–>点
所处的位置信息，电线杆高度及其他相关信息
一条道路–>线
道路长度、宽度、起点、终点及道路等级等相关信息
一个湖泊–>多边形
湖泊的周长、面积和水质等信息

[2]空间数据的特征

空间特征

• 每个空间对象都具有空间坐标，即空间对象隐含了空间分布特征
• 空间数据组织需要考虑它的空间分布特征
• 除了属性索引外，还需要建立空间索引

非结构化特征

• 关系数据库中数据记录是结构化的
• 结构化数据
  • 满足关系模式的范式基本要求，可以用二维表结构来逻辑表达的数据
• 非结构化的数据
  • 不方便用数据库二维逻辑表来表现的数据，包括文本、图片、XML、HTML、音频、视频等
• 空间数据是一种非结构化数据
• 空间实体是不定长的，例如一条弧段可能包含两对坐标点，也有可能10万对坐标点
• 通用的关系数据库管理系统难以直接管理空间数据

空间关系特征

• 空间数据包括空间坐标和拓扑关系
  • 方便空间数据的查询和空间分析(几何对象模型和空间网络模型)

时态特征

• 反映地理实体的状态和演变过程的重要组成部分

多尺度特征

PostGIS 是一个空间数据库。Oracle Spatial 和 SQL Server（2008 或更高版本）也是空间数据库

[3]空间数据库的三大要素

• 空间数据（Spatial Data Type）
• 空间分析（Spatial Analysis）
• 空间索引（Spatial Indexing）

[4]空间数据库vs一般数据库

• 数据量大
  • 一个城市达几十个G，影像达几百个G
  • 在二维空间上划分为块或分幅，在垂直方向上划分为层来进行组织
• 空间数据与属性数据结合
• 应用广泛

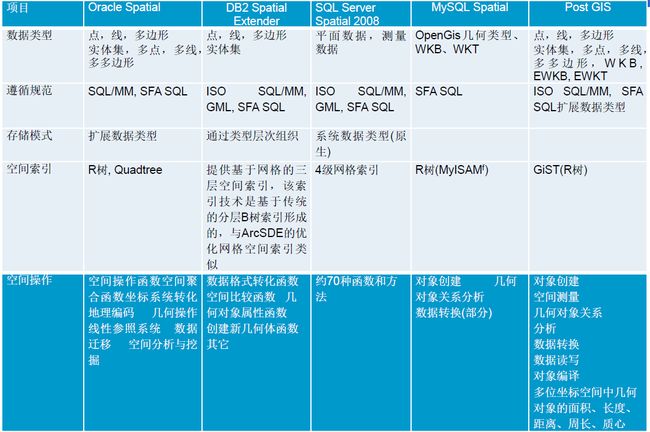
[5]常见的空间数据库管理系统

Spatial Database Management System，SDBMS

[6]空间数据类型

一个普通的数据库有字符串、数字和日期。而空间数据库添加了额外的数据类型来表示地理特征。这些数据类型抽象和封装了边界和维度等空间结构。在许多方面，空间数据类型可以简单地理解为形状geometry。

空间数据类型以分层类型组织。每个子类型都继承其父类型的结构（属性）和行为（方法或函数）。

[7]空间函数

空间数据库提供一组功能来分析几何组件、确定空间关系和操纵几何。这些空间功能作为构建任何空间项目的“工具”。

大多数空间函数可以分为以下五类之一：

1. 转换：在geometry（PostGIS中存储空间信息的格式）和外部数据格式之间转换的函数。
2. 管理：管理有关空间表和 PostGIS 管理的信息的功能。
3. 检索：检索几何的属性和测量值的函数。
4. 比较：比较两个几何的空间关系的函数。
5. 生成：从其他函数生成新几何图形的函数。

[8]postgis简介

PostGIS通过向PostgreSQL添加对空间数据类型、空间索引和空间函数的支持，将PostgreSQL数据库管理系统转换为空间数据库。

[9]空间数据库标准规范

现有空间数据库标准主要有：

• Simple Feature Access SQL, SFA SQL（地理信息简单要素的SQL实现规范）
• SQL Multimedia Part3: Spatial, SQL/MM

SFA SQL

SFA SQL是OGC制定的标准

Simple Feature Access规范的两部分分别为：

• Simple Feature Access - Part 1: Common Architecture（https://www.ogc.org/standards/sfa） —— 定义几何对象的通用架构，描述了通用的简单要素地理集合对象模型，及集合对象的不同表达方式和空间参考系统的表达方式，具有平台独立性。
• Simple Feature Access - Part 2: SQL Option（https://www.ogc.org/standards/sfs） —— 定义了第一部分定义的简单要素模型在数据库中的实现，给出了内模式下几何类型(geometry type)的定义及相关实现。

SFA由OGC于1999年提出，说明了简单地理要素（点，线，多边形等）的对象模型及其发布、存储、读取操作的接口标准。

2005年进一步细化了相关内容，添加了注记文字 (Annotation Text)，将其修订为简单要素访问规范 (Simple Feature Access, SFA)1.1.0版。

2006年10月，推出了SFA 1.2.0版，目前该实现规范已被ISO TC211吸纳为ISO19125系列标准。

目前最新的SFA版本为1.2.1，于2011年推出。

SQL/MM

• PostGIS更符合SFA SQL标准（常用）
• Oracle Spatial更兼容SQL/MM标准

SQL/MM是ISO（International Standard Organization，国际标准化组织）提出的标准，SQL/MM第三部分空间定义了矢量数据存储与检索的相关标准，解释了基于这些数据类型如何使用存储、获取和处理空间数据。

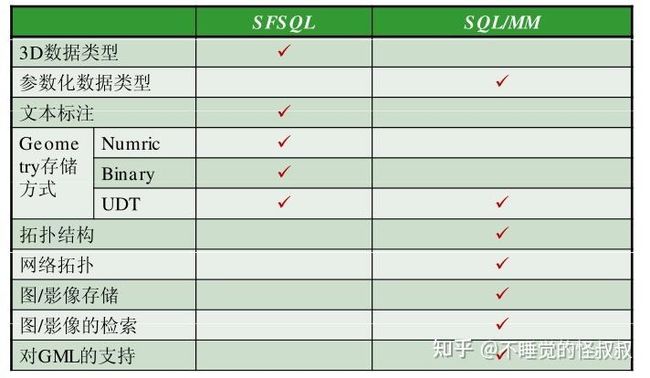
两个标准的对比分析（重点）

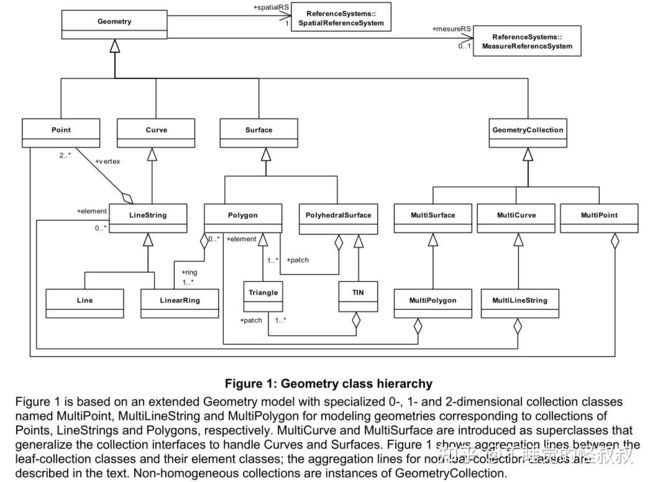
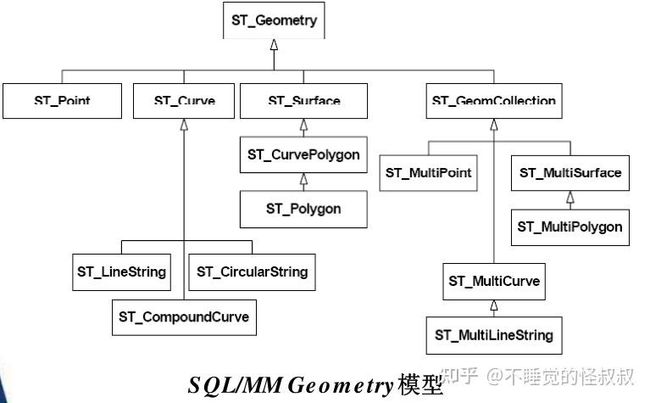
SFA SQL和SQL/MM的Geometry类型总体框架比较近似

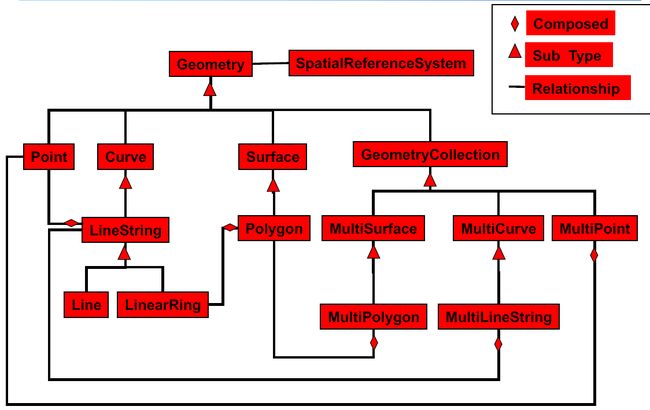
SFA SQL的Geometry类型结构图：（有空间参考系）

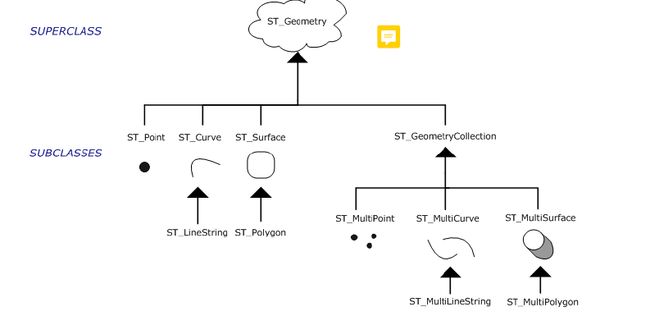
SQL/MM的Geometry类型结构图：

2.几何对象模型

[1]空间数据模型

什么是数据模型？

空间数据模型表达的是空间信息的一种数据组织方式，通常有对象模型、场模型、网络模型等。现有空间数据库系统均是基于某种空间数据模型的。空间数据模型是数据库系统的核心和基础。

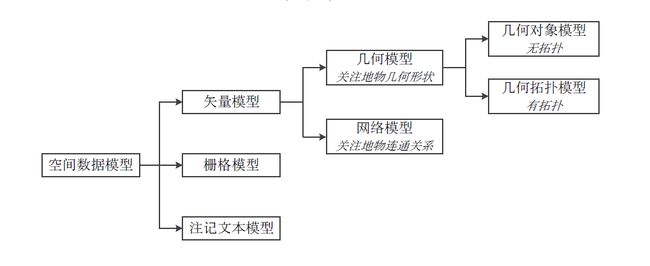
空间数据模型的分类

现有的空间数据库都是基于某种空间数据模型

GIS中常见的两大数据模型：矢量模型和栅格模型

矢量模型

• 利用点、线、多边形的形式来表达现实世界
• 具有定位明显，属性隐含的特点
• 不可再分的最小单元现象称为空间实体
• 空间地物精确形状的几何(geometry)模型
  • 不含拓扑关系的对象(object)模型
  • 包含拓扑关系的拓扑(topo)模型
• 地物连通关系的网络(network)模型

栅格模型

• 以二维矩阵的形式来表示空间地物或现象分布的数据组织方式
• 每个矩阵单位称为一个栅格单元，单元值表示地物或现象的属性数据

注记文字模型

• 注记标签annotation label
• 注记文本annotation text
• 注记尺寸annotation size

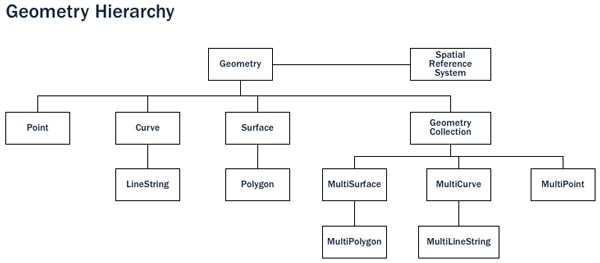
[2]几何对象模型

几何对象模型是空间数据库中最常见、最基础的一个模型

概念模型

可以理解为空间数据类型（同关系型数据库中的实体，属性之类的概念）

• 一个依赖于空间参考系(Spatial Reference System)
• 测量参考系(Measure Reference System)
• 几何(Geometry)类
• 点(Point)：零维几何对象类，代表空间中的一个点，如城市
• 线(Curve)：由点序列描述一维的几何对象类，如街道、管线。相邻两点间的插值方法：线性插值和非线性插值
• 面(Surface)
• 多点(MultiPoint)
• 多线(MultiCurve)
• 多面(MultiPolygon)
• 多曲线(MultiCurve)
• 多折线(MultiLineString)
• 多多边形(MultiPolygon)
• 折线(LineString)：曲线的子类，采用线性插值
• 线段(Line)：折线的特例，只有两个点的线串
• 环线(LineRing)：由折线派生而来，闭合的、不自相交或相切的折线
• 多边形(Polygon)
• 体表面(PolyhedraSurface)
• 三角形(Triangle)
• 不规则三角网(Triangulated irregular network, TIN)
• 几何集合(GeometryCollection)

坐标维数与几何维数的区别：坐标维数为常见（x,y,z)坐标，而几何维数为：几何维度是在一定前提下描述一个几何对象所需的参数个数。例如：“点是零维的、线是一维的、平面是二维的、体是三维的

地理要素(feature)

• 对现实世界空间现象的抽象
• 由几何(geometry)、属性(attribute)、行为(behavior)等三类信息构成
• 地理要素的属性和行为等信息的建模是由应用系统的设计者，根据实际应用需求进行建模
• 几何的建模是数据库管理系统关心的基础问题

理解该模型的几个要点

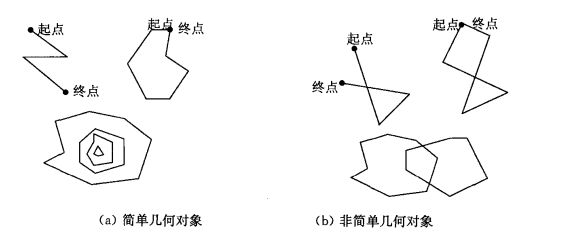
1. OGC仅能表达和处理简单(Simple)的几何对象：简单几何对象是指不自相交的几何对象

2. 任何几何模型都有其边界(boundary)、内部(interior)和外部(exterior)

   • 边界：一个几何实体界限的集合，几何维数是其本身几何形状的维数减一
     • 点：空
     • 线：端点
     • 曲线及其子类：起始点和终止点
     • 多曲线及其子类：各曲线的起始点和终止点
     • 面：构成它的线串
   • 内部：是几何对象除边界外的所有直接位置 (direct position) 的集合
   • 外部：是空间全域与几何闭包之差
     • 任意几何对象外部的维数总是2
     • 所有的几何形状都有外部，即其几何形状的补集

3. 几何对象模型的坐标维数为3，但目前仅能描述二维几何对象

   • z值仅用于记录点在坐标空间中第3个坐标轴的测量值
     • 点用来表示山峰的位置，z值表示该山峰的高度
   • 模型中的体表面(PolyhedralSuface)类和不规则三角网(TIN)类也仅用于表达三维坐标空间中的某个曲面，并不能表达一个真正的三维的体模型
   • 随着空间应用的不断深入，三维几何对象、四维时空对象将是该模型今后需要不断发展和完善的地方

4. M值

   • 点类除了x, y, z坐标外，还有一个M坐标
   • M值是线性参考系统的一个重要的度量值
   • 例如，高速公路上的里程碑点可用其M值表示从高速公路
     起点到当前位置的距离

5. 由于体表面违反了“多边形元素只能相交在有限数量的点上”的规则，所以体表面不是多多边形

6. 不规则三角网格主要用来表达高程或其他状况(如浓度)的表面

   • 用来高程、坡度、坡向的计算，等高线的提取，体积的计算，垂直剖面分析，通视分析等

   • 在OGC的数据模型中，TIN被认为是矢量数据的一种表达方式，而ESRI的GeoDatabase则将其视为一种不同于矢

   • 量表达的另一种空间数据表达方式

几何对象的方法（函数）

分类

• 常规方法

12种方法，概念和方法不难理解

• 常规GIS分析方法

7种方法，基于GIS基础也不难理解

• 空间查询方法

前9种与空间拓扑关系查询有关
后2种是基于线性参考的空间查询方法

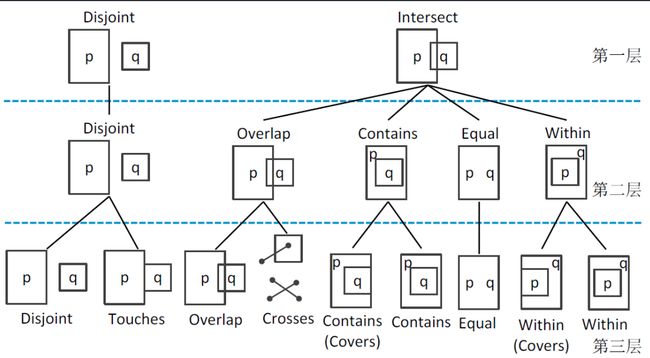
空间拓扑关系

8种空间关系

• 相离(disjoint)

  若 ∩ = ∅，则a和b相离

• 相交(intersects)

  若 ∩ ≠ ∅，则a和b相交

  a.Intersects(b) ↔ !a.Disjoint(b)

• 相等(equals)

  若 ，且 ，则a和b相等

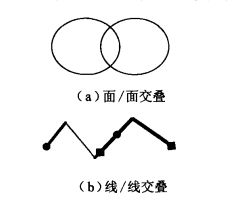
• 交叠(overlaps)

  如Dim(I(a)) = Dim(I(b)) = Dim(I() ∩ ())，且 ∩ ≠ ，同时 ∩ ≠ ，则a和b交叠

  点/点、线/线、面/面交叠关系，没有线/面等交叠关系

  

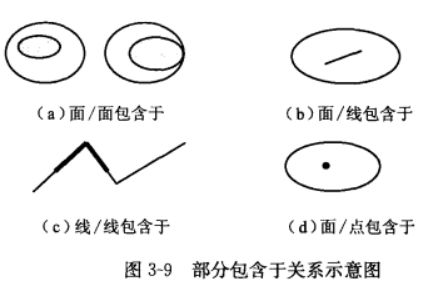
• 包含于(within)
  若 ∩ = ，且I ∩ = ∅，则a包含于b内

  

• 包含(contains)
  若b包含于a，则a包含b
  a.Contains(b) ↔ b.Within(a)

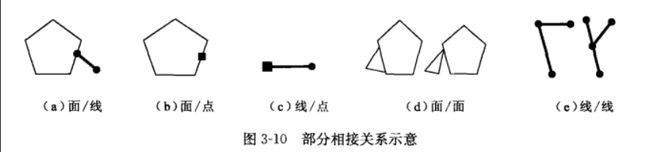
• 相接(touches)
  若I ∩ = ∅，且 ∩ ≠ ∅，则a和b相接
  面/面、线/线、线/面、点/面、点/线相接关系
  但没有点/点相接关系(为什么?)

​

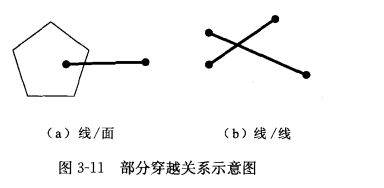
• 穿越(crosses)
  n 若[Dim(I ∩ ) < max(Dim(I(a)), Dim(I(b)))，且Dim(I(b)) !=0， ∩ ≠ ， ∩ ≠ ，则a穿越b
  n OGC定义：I ∩ ≠ ∅ ， ∩ ≠ ， ∩ ≠
  n 点/线、点/面、线/线、线/面穿越关系

​

空间对象的拓扑关系不是非此即彼的，也有一定的分辨精度层次关系

逻辑模型

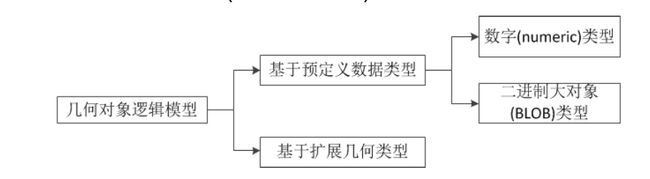
基于概念模型，OGC提出了基于预定义数据类型和基于扩展几何类型的两种实现方法

基于预定义数据类型的实现

• 利用关系数据库中已有的数字(numeric)类型、二进制大对象(BLOB)类型实现空间数据的存储和管理，这些数据类型的解释和维护由DBMS负责、
• 相关空间数据访问方法作为扩展函数嵌入到DBMS中
• 与空间数据引擎(如ArcSDE)的区别

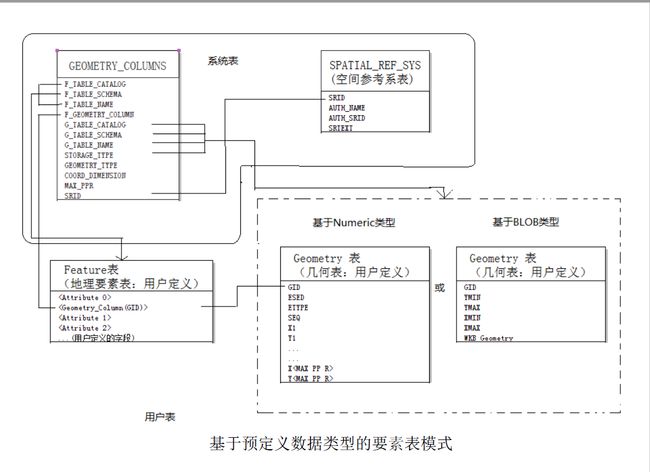
基于numeric和BLOB的实现，要素表(Feature)、几何列表(GEOMETRY_COLUMNS)和空间参考系(SPATIAL_REF_SYS)表的结构都一样，不同之处在于几何(Geometry)表的结构

要素表和几何表是用户表，用于存储空间数据，几何列表(geometry_columns)和空间参考系表是系统表，用于存储用户表的元数据(meta-data)信息

下面为每个表的各字段解析

Feature表:

• 记录一组具有相同属性和行为的地理要素的集合，要素表的列代表要素的属性，而不同的行代表不同的要素
• Geometry_Column列是几何对象的逻辑几何数据类型，其存储的是几何对象的唯一标识(geometry ID, GID)，而几何数据实际存储在Geometry表中，因此，可以将GID作为指针到Geometry表找到其空间数据

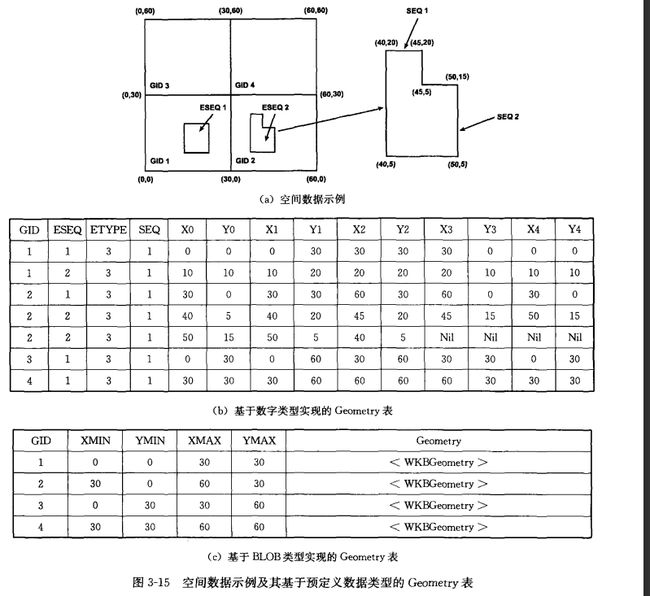
(基于Numeric类型的)Geometry表:

• 将几何类型的空间坐标作为数值对存储在表中，每行最多可存储MAX_PPR个空间坐标
• 若Geometry的空间坐标超过MAX_PPR则折行存储
• 其中的GID是Geometry对象的唯一标识
• 在由多个元素组成的GeometryCollection中ESEQ用于表示不同的元素
• SEQ则用于标识统一Geometry折行存储后的行序列号
• ETYPE用于标识Geometry表中指定的几何对象的类型(如，点、线、面、多点等)

(基于BLOB类型的)Geometry表:

• 将空间数据以WKB(Well-Known Binary Representation)形式存储在名为WKB_Geometry的BLOB类型的字段中，
• 不会出现折行存储Geometry的情况
• 一行存储一个Geometry对象
• 每行GID是该Geometry对象的唯一标识
• YMIN, YMAX, XMIN, XMAX用于存储该对象的四至
• 该表的主码是GID

GEOMETRY_COLUMNS表:

• 记录数据库中所有要素表及其几何列的属性
• 该表的前三列可以唯一标识Feature表
• F_TABLE_CATALOG, F_TABLE_SCHMEA, F_TABLE_NAME分别表示某Feature表所在的目录名、模式名和表名
• F_GEOMETRY_COLUM用于记录前3列值确定的Feature表中
• Geometry列的名字
• G_… 分别表示Geometry表所在的目录名、模式名和表名
• STORAGE_TYPE表示Geometry表的存储类型
• GEOMETRY_TYPE表示Geometry表中几何对象的类型
• COORD_DIMENSION表示几何对象的坐标维数
• MAX_PPR表示每行存储的空间坐标点个数
• SRID描述了Feature表的空间参考系

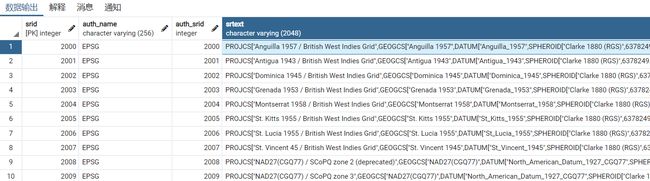
SPATIAL_REF_SYS表

• 记录了该空间数据库所支持的所有空间参考系
• SRID为主码
• AUTH_NAME是空间参考系的名字
• RTEXT是空间参考系的文字描述
  • 4326 – WGS 84 Long Lat
  • 4269 – NAD 83 Long Lat
  • 3395 – WGS 84 World Mercator
  • 2163 – US National Atlas Equal Area

示例

基于数字类型的Geometry表：其中，1 或多个坐标值(X 坐标值）将被表达为 Geometry 表中数值类型的对，每 个几何对象用键(GID) 标识，对象中不同元素元由 ESEQ 标识，每个元素的类型用 ETYPE 标识，每个元素分布在要素表的1或多行中，它们特有的顺序用 SEQ 值标识。对于无用的坐标对应将其全集(X Y) 置为 Nil 。

基于 BOLB 类型的 Geometry 表：它仍用 GID 作为键、用 Geometry 著名二进制表示存储几何对象， Geometry 表包括几何对象的最小边界矩形。这样如有需要，允许构建无真实几何对象结构 访问的空间索引。

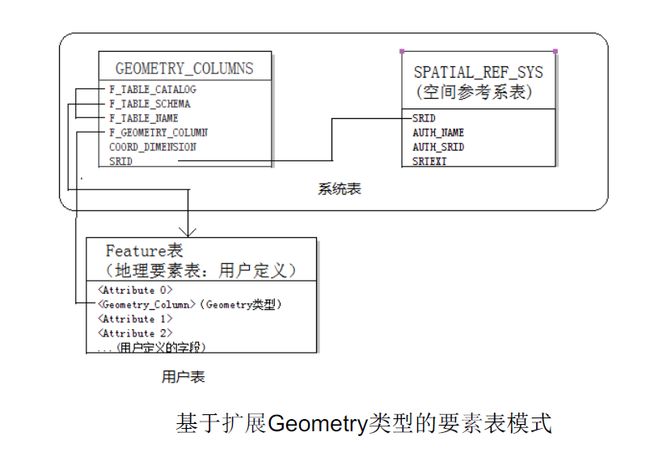
基于扩展几何类型的实现

所谓基于扩展 Geometry 类型的实现就是利用对象关系型数据库中对抽象数据类型的支 持，定义 Geometry 类型及其相关的方法与函数，并用该扩展的 Geometry 类型实现空间数 据的存储与管理。

各表字段解释：

GEOMETRY_COLUMNS和SPATIAL_REF_SYS是系统表，用于存储元数据信息

• 属性解释与上面基于预定义数据类型相同

Feature表是用户表，用于存储空间数据

• 属性数据存在用户定义的Attributes列中

• 空间数据存放在扩展几何类型的Geometry_Column中

创建扩展几何体类型数据示例：

Create Type Geometry As Object (
Private Dimension SmallInt Default -1,
Private CoordinateDimension SmallInt Default 2,
Private Is3D SmallInt Default 3,
Private IsMeasured SmallInt Default 0)
Not Instantiable
Not Final

定义Dimension函数

Method Dimension()
Return SmallInt
Language SQL
Deterministic
Contains SQL
Returns Null On Null Input
……

定义SymDifference函数

Method SymDifference(ageometry Geometry)
Return Geometry
Language SQL
Deterministic
Contains SQL
Returns Null On Null Input
……

物理模型

WKB

在基千 BLOB 的实现方案中，数据库仅将其解释为一个大的二进制串，故空间数据库管理系统的设计者需要考虑此二进制串的物理意义。

SFA SQL 给出了一种较为紧凑的几何数据的二进制方式的存储格式，即 WKB(well-known binary) 。它不仅可用于BLOB中空间对象的存储，还可以用于几何数据二进制流的交换。

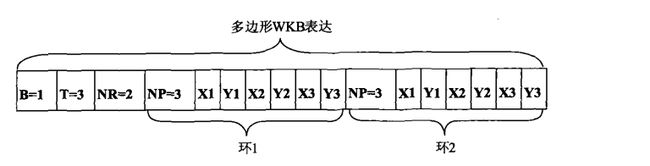
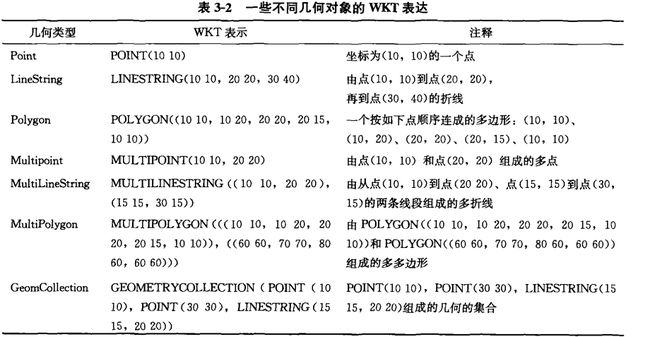
WKB表达

示例：出一个由两个环构成的多边形的 WKB 表达

• SFA SQL给出了一种较为紧凑的几何数据的二进制方式的存储格式
• 数字类型串行化为网络数据表示(network datarepresentation, NDR)或外部数据表示(external datarepresentation, XDR)存储在磁盘上
• NDR(按小Endian方式编码)和XDR(按大Endian方式编码)是两种标准的数字类型二进制编码方式

WKT

• 为在不同环境间交换几何数据， OGC 还提出了一种基于文本格式几何数据交汇标准表 达方法，即 WKT(well-known text) 。（易读）
• OGC也为空间参考系提供了投影、地理和地心三种坐标系的不同WKT表达形式
• SPATIAL_REF_SYS系统表中SRTEXT存储的是空间参考系的WKT表达

以地理坐标系为例，在NAD83水准面(Datum)上的UTM10带被定义为：

PROJCS [“ NAD_198 3_UT M_Zon e_10M”,
< geographic cs>,
PROJECTION [“ Transverse_Mercator”],
PARAMETER [“ False_Easting”, 500000.0],
PARAMETER [“ False_Nothing”, 0.0],
PARAMETER [“ Central_Meridian”, -123.0],
PARAMETER[“ Scale_Factor”, 0.996],
PARAMETER[“ Latitude_Of_Origin”, 0.0],
UNIT [“ Meter”, 1.0]]
#对象依次为水准面、椭球体、本初子午线和测量的角度单位

示例：

注意事项

WKT和WKB只支持二维几何对象的表达，并没有任何有关空间参考系的信息

• 在将几何体的WKT或WKB表达在转换成另一种格式时，空间参考系信息常被丢失，若想保留这些信息，需要单独对其进行处理，同时用setSRID()方法把它们添到几何体中
• 为了避免这一缺点，PostGIS分别扩展形成EWKB和EWKT，不仅可以嵌入集合体的SRID信息，还增加了对3DZ、3DM和4D坐标的支持

3.空间结构化查询语言

• 结构化查询语言(SQL)是关系数据库的标准语言（通用的、功能强大的关系数据库语言）

• 空间结构化查询语言(Spatial Structured QueryLanguage, SSQL)

  • 基于SQL99提供的对象扩展机制，扩充的一种用于实现空间数据的存储、管理、查询、更新与维护的结构化查询语言

  • 由于与地理位置密切，也称为GSQL

• SSQL是基于某种空间数据模型，对标准的SQL进行扩展

  • 空间数据类型的基本操作
  • 描述空间对象间拓扑关系的函数
  • 空间分析与处理的一般操作

• 以PostgreSQL/PostGIS为例

PostGIS Manual Chapter 4, 6, 7http://postgis.net/docs/index.html

查找具体函数定义和说明Chapter 8-13

4,常用开源GIS工具

[1]postgis

原生的postpresql：

• 基本的集合实体类型，如点、线、线段、方形、多边形和圆等
• 函数和操作符实现几何类型的操作和运算
• 空间数据索引R-tree

难以达到GIS要求

• 缺乏复杂的空间类型
• 没有提供空间分析
• 没有提供投影变换功能

此时便诞生了postgis

PostGIS是由Refractions Research公司研发的、对象关系型数据库系统PostgreSQL的一个空间扩展（在某个数据库下添加扩展postgis，该库便成为了空间数据库）下面为postgis的一些好处

• 提供空间对象、空间索引、空间操作函数和空间操作符等空间信息服务功能
• GNU的GPL，即任何人可以自由得到PostGIS的源码并对其做研究和改进

支持PostgreSQL/PostGIS开源GIS产品体系

• 桌面GIS软件QGIS http://www.qgis.org/
• WebGIS服务GeoServer http://geoserver.org
• 支持各种空间格式转换的GDAL http://www.gdal.org/

PostGIS遵循OpenGIS的规范开发，支持OGC规范中的点、线、多边形、多点、多线、多多边形和集合对象集

PostGIS支持所有的对象表达方法，比如WKT和WKB，支持所有的数据存取和构造方法，提供空间分析函数，提供对元数据的支持及其相关的访问函
数，提供一系列用于检测空间对象之间的空间关系的二元谓词，提供空间操作符用于空间数据操作

除OGC规范要求的内容外，PostGIS提供：

• 数据库坐标变换
  • 几何类型通过Transform从一种投影变换到另一种
• 球体长度运算
• 三维几何类型3DZ,3DM and 4D coordinates
• 空间聚集函数
  • 聚集函数Extent返回一系列要素的最小边界矩形
• 栅格数据类型

• PostGIS并未严格地按照对象加方法的形式实现，而是采用对象类型加函数的形式实现
• 早起的PostGIS函数是根据OGC的SFA SQL标准开发，后来OGC为了与SQL/MM兼容，修订了SFASQL标准，形成了SFA SQL以及ISO19125
• 在后续的标准中，空间函数的参数稍有变动，且均已“ST_”(Spatial Type)开头。为此，OGC又根据SFA SQL封装了一套“ST_”开头的函数
• PostGIS常会出现两个功能基本相同的函数，一个以“ST_”开头，另一个则无“ST_”（因为SFA SQL标准的Geometry函数是无ST开头的，而SQL/MM标准的Geometry函数则是有ST开头的）

PostGIS中常用数据类型

• boolean 布尔类型，其值为T或F
• box2d 矩形框类型，由矩形左下角和右上角组成
• box3d 长方体类型，由左前下角和右后上角组成
• bytea 相当于BLOB类型，可变长的二进制值
• integer 字节为4的整数(int4)
• double precision 字节为8的浮点数(float8)
• character varying可变长字符类型，相当于BLOC

Shapefile数据导入

使用PostGIS 2.0 Shapefile and DBF Loader Exporter

使用QGIS连接导入

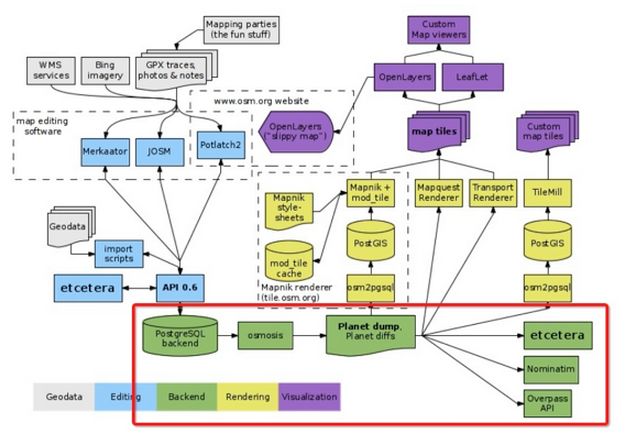
[2]OpenStreetMap

OSM网上地图协作计划，目标是创造一个内容自由且能让所有人编辑的世界地图

OSM数据结构

空间数据和属性数据

• 空间数据
  • Node定义了空间中点的位置
    • node通过经纬度定义了一个地理坐标点
    • 可以height=标示物体所海拔；通过layer= * 和level= * ，可以标示物体所在的地图层面与所在建筑物内的层数；通过place=* 和name=* 来表示对象的名称。同时，way也是通过多个点（node）连接成线（面）来构成的
  • Ways定义了线或区域
    • 通过2-2000个点(nodes)构成了way。way可表示如下3种图形事物：非闭合线(Open polyline)、闭合线(Closedpolyline)、区域(Area)。对于超过2000 nodes的way，可以通过分割来处理
    • Open polyline
      • 非闭合线：收尾不闭合的线段。通常可用于表示现实中的道路、河流、铁路等
    • Closed polyline
      • 闭合线：收尾相连的线。例如可以表示现实中的环线地铁
    • Area
      • 区域：闭合区域。通常使用landuse=* 来标示区域等
  • Relations(可选的)定义了元素间的关系
    • 一个Relation是用来描述两个或多个基元的相互关系(nodes, ways 或者其他的relations)，相互的关系通过role来定义，包括
      • route ：定义公路、自行车道、铁路等
      • 多个多边形：定义area例如建筑、河堤等
      • 边界：装门用来定义行政边界
      • 限制：用于描述限制比如“非左转”
• 属性数据Tags用于描述上述矢量数据基元
  • 标签不是地图基本元素，但是各元素都通过tag来记录数据信息
  • 通过key和value来对数据进行记录
  • 例如，可以通过highway=residential来定义居住区道路；同时，可以使用附加的命名空间来添加附加信息，例如，maxspeed:winter=*就表示冬天的最高限速

OSM数据及下载

osm数据格式：

OSM XML – xml-format provided by the API

PBF – highly compressed, optimized binary format similar to the API

o5m – for high-speed processing, uses PBF coding, has same structure as XML format

OSMJSON – json variant of OSM XML

osm数据下载网站：

GeoFabrik：http://www.geofabrik.de/

Metro Extracts：[http://metro.teczno.com/

)HOT Exports：http://hot.openstreetmap.org/

BBBike：http://extract.bbbike.org/

基于OSM数据搭建一个地图服务

5.矢量数据的定义与操纵

[1]数据定义与插入

创建一个实践表

create table landuse (
    landuse_id integer NOT NULL,
    name varchar(20),
    the_geom geometry, #也可以写成the_geom geometry(Polygon, 4326)
    area double precision,   #面积
    perimeter double precision,  #周长
    constraint landuse_key primary key (landuse_id));

插入数据

例3：将一条新的土地利用数据记录(ID:12; 名称:Timberforest;几何列WKB描述:01010000001DDB93F460BB4241A84E5AC86F455441; 面
积: 47806700; 周长: 34246.2)插入到landuse表中

insert into landuse
values(12, ‘Timber-forest’,
‘01010000001DDB93F460BB4241A84E5AC86F455441’,
47806700, 34246.2);
//等同于
insert into landuse
values(12, ‘Timber-forest’,
ST_GeomFromText(‘Polygon((10 10, 10 20, 20 20, 20 10,
10 10))’, 4326), 47806700, 34246.2);

插入子查询结果（首先建立新表 landuse_ new, 其属性列名与 landuse 相同）
例4：将landuse表中ID号小于15的记录存入表landuse_new中，假设landuse_new属性列只有landuse_id, name,the_geom

insert into landuse_new
select landuse_id, name, the_geom
from landuse
where landuse_id < 15;

[2]管理函数

管理和操纵几何类型的数据表及其元数据

• AddGeometryColumn(varchar,varchar,varchar,int4,varchar,int4)
  • 添加几何字段
  • 参数依次为：表的模式名 ，表名 ，列名（字段名），数据几何类型 ，几何对象类型的维数 （下面的函数参数同理）
• DropGeometryColumn(varchar, varchar, varchar)
  • 删除几何字段
• DropGeometryTable(varchar, varchar)
  • 删除一个空间表

几何属性可以在创建关系时直接创建，也可以再创建关系后，增加几何属性position geometry(xxx, 4326)AddGeometryColumn

• Probe_Geometry_Columns()
  • 检查数据库几何字段并在系统表geometry_columns表中归档
• ST_SetSRID(geometry, int4)
  • 设置几何对象的空间参考
• UpdateGeometrySRID(varchar, varchar, int4)
  • 更新空间表的空间参考
• Update_Geometry_Stats(varchar, varchar)
  • 更新空间表的统计信息

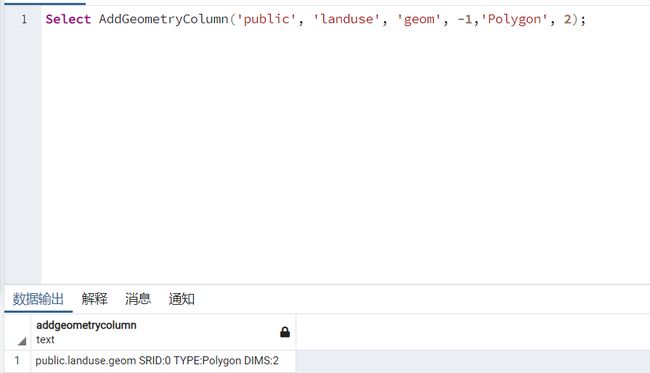
例5：在landuse表中添加一个新的几何字段

Select AddGeometryColumn('public', 'landuse', 'geom', -1,'Polygon', 2)

[3]构造函数

根据给定的几何描述，构造相应几何对象

• 根据WKT/WKB表达，生成多几何对象

  • ST_GeomCollFromText(text, [])
  • ST_GeomCollFromWKB(bytea, [])

• 根据GML/WKT/WKB表达，生成几何对象

  • ST_GeomFromGML
  • ST_GeomFromText(构造几何对象建议使用ST_GeomFromText(‘WKT’, 4326)
  • ST_GeomFromWKB

• 根据输入的多点/WKT/WKB表达，生成线串

  • ST_LineFromMultiPoint(geometry)
  • ST_LineFromText(text, [])
  • ST_LineFromWKB(bytea, [])

• 创建一个A为左下角点、B为右上角点的box2d对象

  • ST_MakeBox2D(geometry A, geometry B)

• 根据给定的两个点对象，生成一条线段

  • ST_MakeLine(geometry, geometry)

• 创建一个2D、3D或4D坐标空间中的点对象

  • ST_MakePoint(float8, float8, [], [])

• 创建一个带有x, y和M值的点对象

  • ST_MakePoint(float8, float8, float8)

• 创建一个多边形（输入参数中的几何对象必须是封闭的）

  • ST_MakePolygon(geometry, [])

• 基于WKT/WKB表达，生成多点/多线/多多边形

  • ST_MPoint(Line)(Poly)FromText(text, [])

• 根据给定的左边对，生成点

  • ST_Point(float, float)

• 根据WKT/WKB表达，生成多边形

  • ST_PolyFromText(text, [])
  • ST_PolyFromWKB(bytea, [])

• 根据给定的线串、SRID（空间参考） ，生成多边形

  • ST_Polygon(geometry, integer)

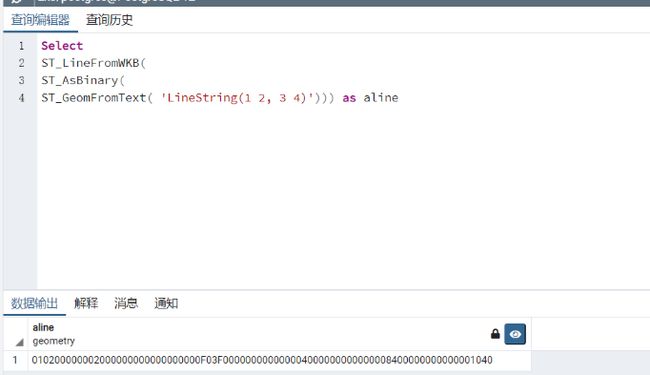
示例：构造名为aline的LineString(1 2, 3 4)几何对象

Select
ST_LineFromWKB(
ST_AsBinary(
ST_GeomFromText( 'LineString(1 2, 3 4)'))) as aline

• 其中， ST _ AsBinary 的作用将 Geometry 类型转换为WKB类型的函数

• ST _GeomFromText 的第一个参数为文本类型，是某个几何对象的 WKT 描述；

• ST_LineFrom WKB 第一个参数为长二进制类型，是某个几何对象的 WKB 述。他们的第二个参数均为可选参数，一般为空间参考 (SRID) 所对应的整数值。在缺省的 情况下， SRID 取值为-1

[4]访问函数

注意：

• 哪些函数适应LineString / Polygon，哪些适用MultiLineString /MultiPolygon

• 新版本可能对函数进行更新，增加或减少功能，例如ST_StartPoint在2.0.0之后不支持single geometryMultiLineString。函数在具体使用时查看适用版本的帮助文档

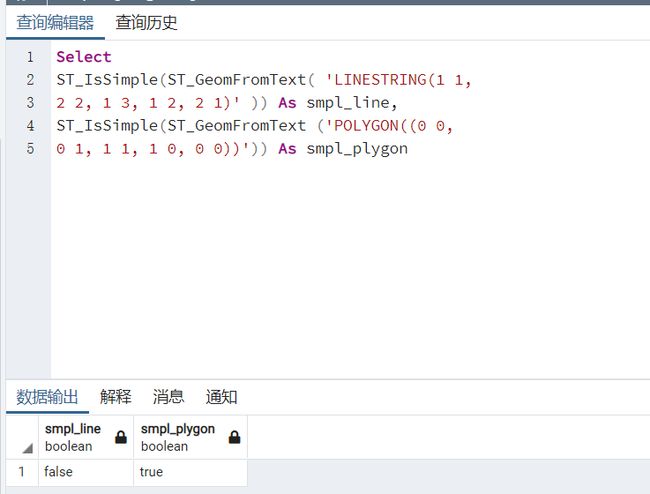
示例：用ST_IsSimple函数判断下面几何对象是否是简单对象

Select
ST_IsSimple(ST_GeomFromText( 'LINESTRING(1 1,2 2, 1 3, 1 2, 2 1)' )) As smpl_line,
ST_IsSimple(ST_GeomFromText ('POLYGON((0 0,0 1, 1 1, 1 0, 0 0))')) As smpl_plygon

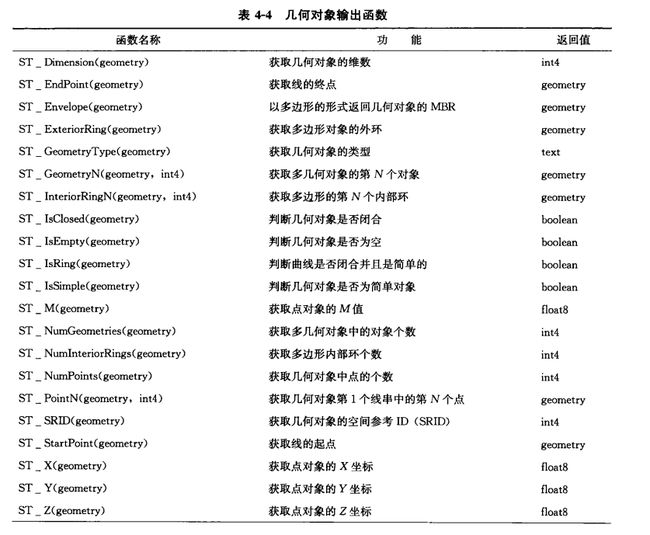
[5]输出函数

按不同格式的要求输出几何对象

• PostGIS按WKB, WKT, EWKB, EWKT, GeoJSON, GML, KML,SVG, 用little-endian或bigendian编码的HEXEWKB等格式输出几何对象
• ST_AsText/AsBinary/AsEWKB/AsEWKT/AsGeoJson/AsGML/AsHEXEWKB/AsKML/AsSVG

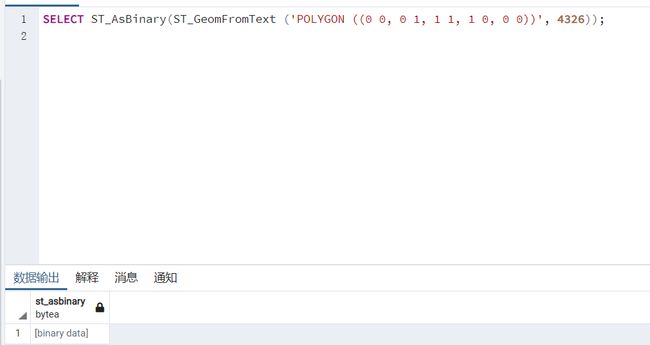
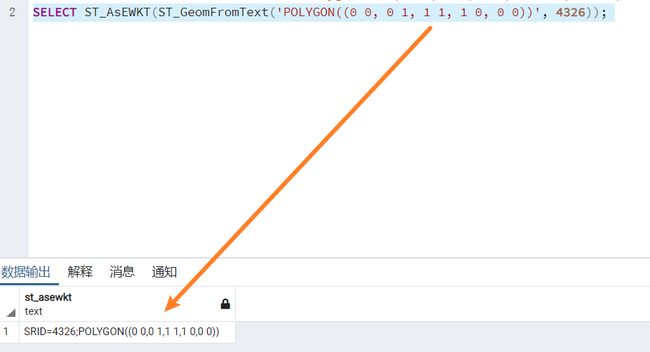
示例：以Polygon((0 0, 0 1, 1 1, 1 0, 0 0))为例，分别按二进制、EWKT、SVG的格式输出

SELECT ST_AsBinary(ST_GeomFromText ('POLYGON ((0 0, 0 1, 1 1, 1 0, 0 0))', 4326));	

SELECT ST_AsEWKT(ST_GeomFromText('POLYGON((0 0, 0 1, 1 1, 1 0, 0 0))', 4326)); 

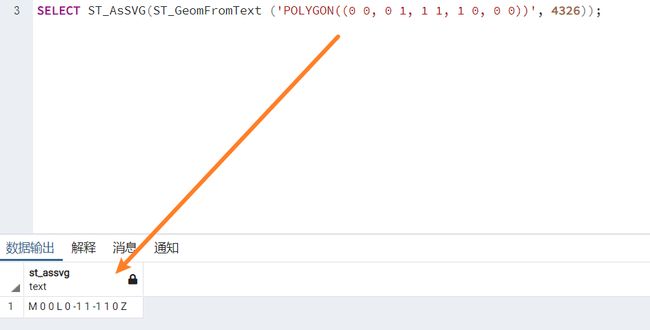
SELECT ST_AsSVG(ST_GeomFromText ('POLYGON((0 0, 0 1, 1 1, 1 0, 0 0))', 4326)); 

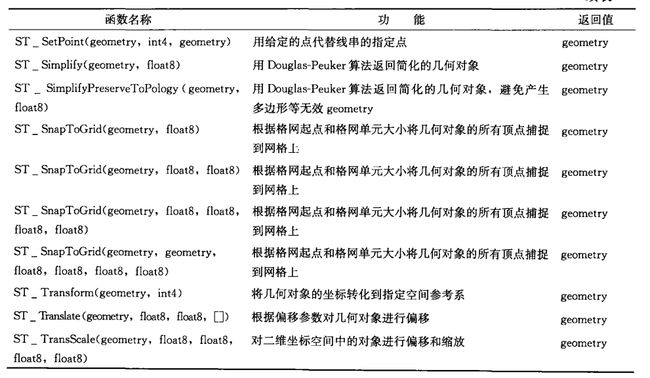
[4]编辑函数

编辑函数用于增加、删除、修改几何对象的坐标信息

示例1：使用ST_Force_Collection函数将原先的Geometry数据类型转换为GeometryCollection

SELECT ST_AsEWKT(ST_Force_Collection('POLYGON((0 0 2, 0 5 2, 5 0 2, 0 0 
2), (1 1 2, 3 1 2, 1 3 2, 1 1 2))'));

示例2：将例1中的多边形用ST_ForceRHR进行强制转换，使其坐标排列顺序符合RHR

Select ST_AsEWKT(
    ST_Force_RHR(
    'Polygon((0 0 2, 0 5 2, 5 0 2, 0 0 2),
    	(1 1 2, 3 1 2, 1 3 2, 1 1 2))'));

示例3：对三维坐标空间中的几何对象进行仿射变换的函数ST_Affine，共13个参数，图形学4X4的变换矩阵，将一条线沿Z轴方向旋转a弧度

Select ST_AsEWKT(ST_Affine(the_geom, cos(a), -
    sin(a), 0, sin(a), cos(a), 0, 0, 0, 1, 0, 0, 0)) As
    using_Affine
From (Select ST_GeomFromEWKT( 'LINESTRING(1
    2 3, 1 4 3)') As the_geom) As HAHA

[4]几何处理函数

获取一些衍生的几何对象，达到不同应用所要求的数据

• ST_Buffer 获取几何对象的缓冲区

• ST_Boundary 获取几何对象的边界

• ST_Centroid 获取几何对象的质心

• ST_ConvexHull 获取几何对象的凸包

• ST_Difference 获取A去除B的几何形状

• ST_Intersection 获取两个几何对象相交部分

• ST_MemUnion

  • 返回值与ST_Union相同，区别是该函数是内存友好的，即用较少的内存和较长的时间完成合并操作

• ST_PointOnSurface 返回曲面上的点

• ST_Shift_Longitude 使经度在0-360之间

• ST_SymDifference 获取A和B互补相交部分

• ST_Union 返回A和B合并后的几何

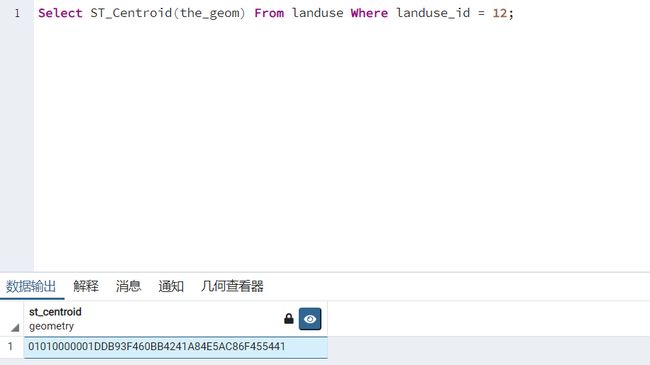
示例1：获取土地利用表landuse中ID号为12的几何对象的质心

Select ST_Centroid(the_geom) From landuse Where landuse_id = 12;

示例2:为土地利用数据表landuse中ID号为12的几何对象建立缓冲区距离为3的缓冲区(ST_Buffer(geometry, float8, [int4]) 可选参数[int4]表示生成缓冲区的一个1/4的圆弧内的点，默认为8)

Select ST_Buffer(the_geom, 3) From Landuse Where Landuse_id = 12

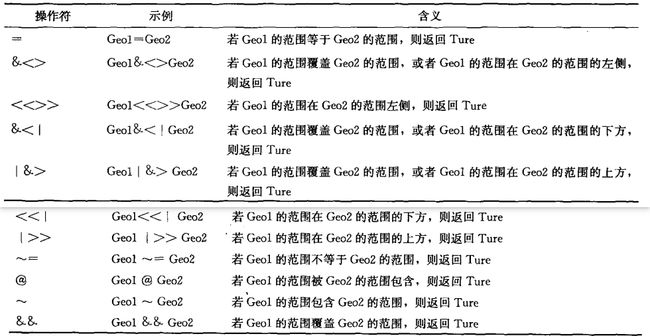
[4]操作符

正如属性数据的">"、"＝＂、＂<”等操作符一样， PostGIS 也定义了一些空间操作符。

与几何操作不同的是：操作符 进行空间操作的对象必须有空间索引才行，也就是说空间操作符是与空间索引绑定的。

示例：

Select tbla.column1, tblb.column1, tbla.column2 &&
tblb.column2 As overlaps
From (Values,
(1, ‘Linestring(0 0, 2 2)’::geometry),
(2, ‘Linestring(0 1, 0 3)’::geometry)) As tbla,
(Values,
(3, ‘Linestring(1 1, 3 5)’::geometry) As tblb

[4]空间关系函数

用于判断两几何对象的拓扑关系

• ST_Contains 判断A是否包含B

• ST_Covers 判断A是否覆盖B

• ST_CoveredBY 判断B是否覆盖A

• ST_Crosses 判断A和B是否相互穿过

• ST_Disjoint 判断A和B是否相离

• ST_DWithin 判断A和B距离是否在给定值内

• ST_Equals 判断A和B是否相等

• ST_Intersects 判断A和B是否相交

• ST_Overlaps 判断A和B是否重叠

• ST_Relate判断A和B是否符合给定的9交模型矩阵

• ST_Relate 获取A和B间的关系DE-9IM

• ST_Touches 判断A和B是否相接

• ST_Within 判断A是否被B包含

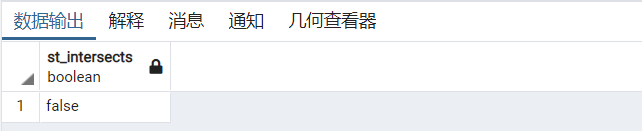
示例：判断两个多边形对象Polygon((1 1, 2 1, 2 3, 11)), Polygon((3 0, 3 2, 4 0, 3 0))间是否相交

Select ST_Intersects(
ST_GeomFromText('Polygon((1 1, 2 1, 2 3, 1 1))'),
ST_GeomFromText('Polygon((3 0, 3 2, 4 0, 3 0))'))

[4]量测函数

获取几何对象的各类测量值

• ST_Area 计算几何对象的面积

• ST_Azimuth 计算两点构成的方位角

• ST_Distance 计算两个几何对象的距离

• ST_Distance_Sphere计算两个几何对象的球迷距离（单位为米），地球半径取值为6370986米

• ST_Distance_Spheroid计算地球曲面上两点间的最短距离，ST_Distance_Sphere速度更快，ST_Distance_Spheroid准确度更高

• ST_Length2d 计算二维坐标距离

• ST_Length3d 计算三维坐标距离

• ST_Length_Spheroid根据给定的地球椭球参数，计算几何对象在地球曲面上的长度

• ST_Max_Distance 计算两个对象间的最大距离

• ST_Perimeter 计算二维坐标空间的周长

• ST_Perimeter3d 计算三维坐标空间的周长

注意：测量函数，如距离，长度，面积等，单位与空间参考系相关

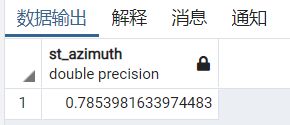
示例1：求两点(0 0)和(1 1)间的方位角

Select ST_Azimuth(ST_GeomFromText('Point(0 0)'),ST_GeomFromText('Point(1 1)'));

示例2：计算两点在GRS_1980地球椭球体下的曲面距离

Select ST_Distance_Spheroid(ST_Centroid(the_geom),ST_GeomFromText('Point(-118, 38)'),'SPHERO ID["GRS_1980", 6378137, 298.257222101]') from landuse;

[4]线性参考

获取线性参考系下的部分几何对象，只对点和线数据有效

• ST_Line_Interpolate_Point 插值点
• ST_Line_Locate_Point 计算位置参数
• ST_Line_Substring 计算线段
• ST_Locate_Along_Measre返回与给定量测值的几何对象
• ST_Locate_Between_Measure返回与给定量测值匹配的几何对象

示例：点在线串30%的位置

Select ST_AsEWKT(ST_Line_Interpolate_Point
(the_line, 0.30))
From (Select ST_GeomFromEWKT(
‘Linestring (25 30, 80 100, 150 210)’) as the_line)
As HOHO
结果: (65.666222484043, 81.7570104342365)

[4]其他函数

• ST_Accum 构造一个几何对象数组

• ST_Box2d 获取几何对象二维中的边界

• ST_Box3d 获取几何对象三维中的边界

• ST_Estimated_Extent估计一个空间数据表的边界范围

• ST_Expand 扩大几何对象

• ST_Mem_Size 获取几何对象使用的内存大小

• ST_Point_Inside_Circle判断点是否在圆内

• ST_Summary获取几何对象的文本概要信息

• ST_XMin, ST_XMax

• ST_YMin, ST_YMax

• ST_ZMin, ST_Zmax

  • 获取X,Y,Z最小值和最大值

示例：估计土地利用数据表landuse的边界范围，以及the_geom字段占用的内存大小的空间查询语句

Select ST_Estimate_Extent('public', 'landuse',
'the_geom')
Select SUM(ST_Mem_Size(the_geom) From landuse

总结

• 查看PostGIS帮助文档-
  • http://postgis.net/docs/reference.html
• 函数定义和描述说明，适用于单个几何对象，还是多个几何集合
• 注意不同版本之间的函数差异，如ST_StartPoint
• 创建空间属性
  • 创建关系时直接创建，如pos geometry(Point, 4326)，增加几何类型和空间参考系
  • 创建关系后增加几何属性，使用AddGeometryColum，注意没有ST_
• 创建空间数据
  • 建议使用ST_GeomFromText(‘几何对象WKT表示’, 4326)
• 空间数据查询– 选择正确的函数解决问题，选择高效的函数提高效率
  • ST_Distance, ST_Length, ST_Area等单位与空间参考系相关
  • ST_Within和ST_DWithin的差异，ST_Distance和ST_DWithin的相互转换