Tarjan 求有向图的强连通分量

Tarjan 算法与有向图的连通性

Tarjan 算法是基于对图进行深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个栈，回溯时可以判断栈顶到栈中的节点是否构成一个强连通分量。

Robert E. Tarjan

Robert E. Tarjan（罗伯特·塔扬，1948~），生于美国加州波莫纳，计算机科学家。

Tarjan 发明了很多算法结构。不少他发明的算法都以他的名字命名，以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法，求 LCA（Lowest Common Ancestor，最近公共祖先）的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。

我们这里要介绍的是在有向图中求强连通分量的 Tarjan 算法。

在正式介绍 Tarjan 算法前，有一些概念我们还需要先了解一些概念。

前置概念

给定有向图 G=(V,E)G=(V,E)，若存在 r∈Vr∈V，满足从 rr 出发能够到达 VV 中所有的点，则称 GG 是一个“流图”(Flow Graph)，记为 (G,r)(G,r)，其中 rr 称为流图的 源点。

与无向图的深度优先遍历类似，我们也可以定义“流图”的搜索树和时间戳的概念：
在一个流图 (G,r)(G,r) 上从 rr 出发进行深度优先遍历，每个点只访问一次。所有发生递归的边 (x,y)(x,y)（换言之，从 xx 到 yy 是对 yy 的第一次访问）构成一棵以 rr 为根的树，我们把它称为流图 (G,r)(G,r) 的 搜索树。

同时，在深度优先遍历的过程中，按照每个节点第一次被访问的时间顺序，依次给予流图中 NN 节点 1\sim N1∼N 的整数标记，该标记被称为 时间戳，记为 dfn[x]dfn[x]。容易知道：一个结点的子树内结点的 dfndfn 都大于该结点的 dfndfn；

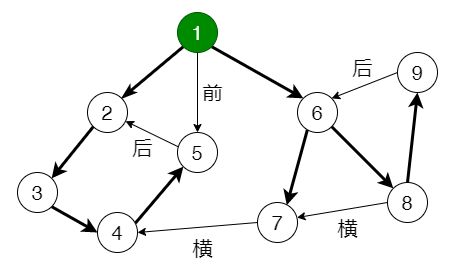
流图中的每条有向边 (x,y)(x,y) 必然是以下四种之一（不一定全部出现）：

1. 树枝边（tree edge），指搜索树中的边，即 xx 是 yy 的父节点。
2. 前向边（back edge），指搜索树中 xx 是 yy 的祖先节点。
3. 后向边（cross edge），指搜索树中 yy 是 xx 的祖先节点。
4. 横叉边（forward edge），指除了以上三种情况之外的边，它一定满足 dfn[y]

下图画出了一个“流图”以及它的搜索树、时间戳、边的分类。圆圈中的数字是时间戳。粗边是树枝边，并构成一棵搜索树。前向边、后向边与横叉边用第一个汉字标注。

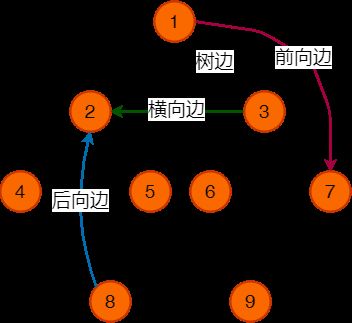
另外一个例子：

我们考虑 搜索树（DFS 生成树）与强连通分量之间的关系。

如果结点 uu 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 uu 为根的子树中。结点 uu 被称为这个强连通分量的根。

反证法：假设有个结点 vv 在该强连通分量中但是不在以 uu 为根的子树中，那么 uu 到 vv 的路径中肯定有一条离开子树的边。但是这样离开子树的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 uu 是第一个访问的结点矛盾了。得证。

有向图的强连通分量

Tarjan 算法的核心原理

给定一张有向图。若对于图中任意两个节点 x,yx,y 之间都连通，也就是既存在从 xx 到 yy 的路径，也存在从 yy 到 xx 的路径，则称该有向图是“强连通图”。

有向图的极大强连通子图被称为“强连通分量”，简记为 SCC（Strongly Connected Components），也就是再增加任意一条图中的边都无法构成强连通子图。此处“极大”的含义与无向图中的双连通分量“极大”的含义类似。

Tarjan 算法基于有向图的深度优先遍历，能够在 线性时间内 求出一张有向图的各个强连通分量。

一个“环”一定是强连通图。如果既存在从 xx 到 yy 的路径，也存在从 yy 到 xx 的路径，那么 x,yx,y 显然在一个环中。因此，Tarjan 算法的基本思路就是对于每个点，尽量找到与它一起能构成环的所有节点。

容易发现，“前向边”(x,y)(x,y) 没有什么用处，因为搜索树上本来就存在从 xx 到 yy 的路径。“后向边”(x,y)(x,y) 非常有用，因为它可以和搜索树上从 yy 到 xx 的路径一起构成环。“横叉边”(x,y)(x,y) 视情况而定，如果从 yy 出发能找到一条路径回到 xx 的祖先节点，那么 (x,y)(x,y) 就是有用的。
为了找到通过“后向边”和“横叉边”构成的环，Tarjan 算法在深度优先遍历的同时维护了一个栈。当访问到节点 xx 时，栈中需要保存以下两类节点:

1. 搜索树上 xx 的祖先节点，记为集合 anc(x)anc(x)。 设 y\in anc(x)y∈anc(x)。若存在后向边 (x, y)(x,y)，则 (x,y)(x,y) 与 yy 到 xx 的路径一起形成环。
2. 已经访问过，并且存在一条路径到达 anc(x)anc(x) 的节点。 设 zz 是一个这样的点，从 zz 出发存在一条路径到达 y\in anc(x)y∈anc(x)。若存在横叉边 (x,z)(x,z)，则 (x,z)(x,z)、zz 到 yy 的路径、yy 到 xx 的路径形成一个环。

综上所述，栈中的节点就是能与从 xx 出发的“后向边”和“横叉边”形成环的节点。进而可以引入“追溯值”的概念。

追溯值

设 subtree(x)subtree(x) 表示流图的搜索树中以 xx 为根的子树。xx 的追溯值 low[x]low[x] 定义为 xx 或 xx 的子树能够回溯到的最早的栈中节点的 dfndfn 值。也就是满足以下条件的节点的最小时间戳：

1. 该点在栈中。
2. 存在一条从 subtree(x)subtree(x) 出发的有向边，以该点为终点。

容易知道，从根开始的一条路径上的 dfndfn 严格递增，lowlow 严格非降；

根据定义，Tarjan 算法按照以下步骤计算“追溯值”：

1. 当节点 xx 第一次被访问时，把 xx 入栈，初始化 low[x]= dfn[x]low[x]=dfn[x]。

2. 扫描从 xx 出发的每条边 (x,y)(x,y)。
   (1) 若 yy 没被访问过，则说明 (x,y)(x,y) 是树枝边，xx 是 yy 的父节点，递归访问 yy，从 yy 回溯之后，令 low[x]= \min(low[x], low[y])low[x]=min(low[x],low[y])。
   (2) 若 yy 被访问过并且 yy 在栈中，则说明 (x,y)(x,y) 是后向边或指向栈中节点的横叉边，令 low[x]= \min(low[x],dfn[y])low[x]=min(low[x],dfn[y])。

3. 从 xx 回溯之前，判断是否有 low[x] = dfn[x]low[x]=dfn[x]。若成立，则不断从栈中弹出节点，直至 xx 出栈。

下图中的中括号 [][] 里的数值标注了每个节点的“追溯值”lowlow。读者可以尝试在图中模拟 lowlow 的计算过程。

强连通分量判定法则

在追溯值的计算过程中，若从 xx 回溯前，有 low[x]= dfn[x]low[x]=dfn[x] 成立，则栈中 xx 和栈中 xx 之和到栈顶的所有节点构成一个强连通分量。

当 dfn[u]=low[u]dfn[u]=low[u] 时，以 uu 为根的搜索子树上所有结点构成一个强连通分量。

简要证明：

大致来说，在计算追溯值的第 33 步，如果 low[x] = dfn[x]low[x]=dfn[x]，那么说明 subtree(x)subtree(x) 中的节点不能与栈中其他节点一起构成环。另外，因为横叉边的终点时间戳必定小于起点时间戳，所以 subtree(x)subtree(x) 中的节点也不可能直接到达尚未访问的节点（时间戳更大）。综上所述，栈中从 xx 到栈顶的所有节点不能与其他节点一起构成环。

又因为我们及时进行了判定和出栈操作，所以从 xx 到栈顶的所有节点独立构成一个强连通分量。

详细证明：

在任何深度优先搜索中，同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说，强连通分量一定是有向图的某一棵深度优先搜索树的子树的子集。

可以证明，当一个点既是强连通子图 11 中的点，又是强连通子图 22 中的点时，它是强连通子图11 UU 图 22 中的点。

这样，我们用 lowlow 值记录该点所在强连通子图对应的搜索子树的根结点的 dfndfn 值。注意，该子树中的元素在栈中一定是相邻的（因为我们及时进行了判定和出栈操作），且根结点在栈中一定位于所有子树元素的最下方。

强连通分量是由若干个环组成的。所以，当有环形成时(也就是搜索的下一个点已在栈中),我们将这一条路径的 lowlow 值统一，即这条路径上的点属于同一个强连通分量（合并了两个强连通子图）。
如果遍历完整棵搜索树后，某个点的 dfndfn 值等于 lowlow 值，则它是该搜索子树的根。这时，它以上（包括它自己）一直到栈顶的所有元素组成一个强连通分量。

参考代码：

下面的程序实现了 Tarjan 算法，求出数组 cc，其中 c[x]c[x] 表示 xx 所在的强连通分量的编号。另外，它还求出了 vector 数组 sccscc，scc[i]scc[i] 记录了编号为 ii 的强连通分量中的所有节点。整张图共有 cntcnt 个强连通分量。

#include
using namespace std;
const int N = 1e5+5, M = 1e6+5;
int n, m, num, top, cnt;  // num: 强连通分量编号
// ins[i]: i 是否在栈中 c[i]: i 所属强连通分量编号
int stk[N], ins[N], c[N];
int dfn[N],low[N];
vector scc[N];
vector g[N];

void tarjan(int u) {
    dfn[u] = low[u] = ++num;
    stk[++top] = u;   // 首次访问，入栈
    ins[u] = 1;         // 标记在栈中
    for (auto v : g[u]) {  // 枚举每条出边
        if (!dfn[v]) {   // 节点 v 未被访问过
            tarjan(v);   // 继续向下找
            low[u] = min(low[u],low[v]); // (u,v) 是树枝边
        }
        else if(ins[v]) {  // (u,v) 是后向边或横叉边， 结点 v 还在栈内，即 v 不属于任何强连通分量
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]) {  // 结点 u 是强连通分量的根
        cnt++; int v;
        do {
            v = stk[top--], ins[v] = 0; // 将 v 出栈，为该强连通分量中一个顶点
            c[v] = cnt;
            scc[cnt].push_back(v);  
        } while(u != v);
    }
}
int main() {
    cin >> n >> m;
    for(int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        g[x].push_back(y);
    }
    for(int i = 1; i <= n; i++) {
        if(!dfn[i])
            tarjan(i);
    }
    cout << cnt << endl;
    for(int i = 1; i <= cnt; i++) {
        cout << i << ":";
        for(auto u : scc[i]) {
            cout << u << ' ';
        }
        cout << endl;
    }
    // 
}

Copy

上面示例图的输入

9 13
1 2
1 5
1 6
2 3
3 4
4 5
5 2
6 7
6 8
7 4
8 7
8 9
9 6

Copy

时间复杂度分析

可以发现，在运行 Tarjan 算法过程中，每个顶点都被访问了一次，且只进出一次栈，每条边也只被访问了一次，所以该算法的时间复杂度为 O(n + m)O(n+m)。

应用

1. 有向图的缩点

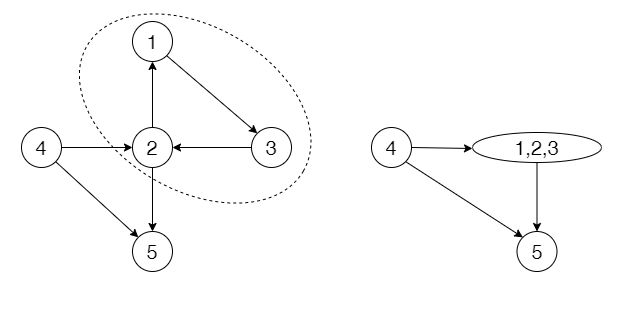
我们可以将一张图的每个强连通分量都缩成一个点。

将同一个强连通分量中的点缩成一个新的节点，对于两个新节点 a,ba,b，它们之间有边相连，当且仅当存在两个点 uu 属于 aa，vv 属于 bb，且  \in E∈E。例如下图。

经过缩点之后的图会变成一个有向无环图（DAG），这样就可以进行拓扑排序以及更多其他操作。

举个简单的例子，求一条路径，可以经过重复结点，要求经过的不同结点数量最多。

下面代码对 SCC 执行缩点过程，并把新得到的有向无环图保存到另一个邻接表中。

vector gn[N];
// 在 main 中
for(int u = 1; u <= n; u++) {
    for(auto v : g[u]) {
        if(c[u] != c[v])     // 不在同一强连通分量中，边不会被缩点缩掉
            gn[u].push_back(c[u], c[v]);
    }
}

Copy

2. 解决 2-SAT 问题

后续讲解。

练习题

• P3990 「一本通 3.5 例 1」受欢迎的牛 - TopsCoding —— 缩点 模板题
• P4791 IOI1996 Network of Schools 学校网络 - TopsCoding —— 缩点+统计入度和出度
• P3992 「一本通 3.5 练习 2」消息的传递 - TopsCoding —— 同上
• P3994 「一本通 3.5 练习 4」搬运计划 - TopsCoding —— 缩点 + 求最长路
• P3991 「一本通 3.5 例 2」最大半连通子图 - TopsCoding —— 缩点+DAG上DP

---

Kosaraju 算法

Kosaraju 算法最早在 1978 年由 S. Rao Kosaraju 在一篇未发表的论文上提出，但 Micha Sharir 最早发表了它。

该算法依靠两次简单的 DFS 实现：

第一次 DFS，选取任意顶点作为起点，遍历所有未访问过的顶点，并在回溯之前给顶点编号，也就是后序遍历。

第二次 DFS，对于反向后的图，以标号最大的顶点作为起点开始 DFS。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的结点，选取标号最大的，重复上述过程。

两次 DFS 结束后，强连通分量就找出来了，Kosaraju 算法的时间复杂度为 O(n+m)O(n+m)。

实现

// g 是原图，g2 是反图
void dfs1(int u) {
  vis[u] = true;
  for (int v : g[u])
    if (!vis[v]) dfs1(v);
  s.push_back(u);
}

void dfs2(int u) {
  color[u] = sccCnt;
  for (int v : g2[u])
    if (!color[v]) dfs2(v);
}

void kosaraju() {
  sccCnt = 0;
  for (int i = 1; i <= n; ++i)
    if (!vis[i]) dfs1(i);
  for (int i = n; i >= 1; --i)
    if (!color[s[i]]) {
      ++sccCnt;
      dfs2(s[i]);
    }
}

Copy

Garbow 算法

Garbow 算法是 Tarjan 算法的另一种实现，Tarjan 算法是用 dfndfn 和 lowlow 来计算强连通分量的根，Garbow 维护一个节点栈，并用第二个栈来确定何时从第一个栈中弹出属于同一个强连通分量的节点。从节点 ww 开始的 DFS 过程中，当一条路径显示这组节点都属于同一个强连通分量时，只要栈顶节点的访问时间大于根节点 ww 的访问时间，就从第二个栈中弹出这个节点，那么最后只留下根节点 ww。在这个过程中每一个被弹出的节点都属于同一个强连通分量。

当回溯到某一个节点 ww 时，如果这个节点在第二个栈的顶部，就说明这个节点是强连通分量的起始节点，在这个节点之后搜索到的那些节点都属于同一个强连通分量，于是从第一个栈中弹出那些节点，构成强连通分量。

实现

int garbow(int u) {
  stack1[++p1] = u;
  stack2[++p2] = u;
  low[u] = ++dfs_clock;
  for (int i = head[u]; i; i = e[i].next) {
    int v = e[i].to;
    if (!low[v])
      garbow(v);
    else if (!sccno[v])
      while (low[stack2[p2]] > low[v]) p2--;
  }
  if (stack2[p2] == u) {
    p2--;
    scc_cnt++;
    do {
      sccno[stack1[p1]] = scc_cnt;
      // all_scc[scc_cnt] ++;
    } while (stack1[p1--] != u);
  }
  return 0;
}

void find_scc(int n) {
  dfs_clock = scc_cnt = 0;
  p1 = p2 = 0;
  memset(sccno, 0, sizeof(sccno));
  memset(low, 0, sizeof(low));
  for (int i = 1; i <= n; i++)
    if (!low[i]) garbow(i);
}

Copy