树结构--介绍--二叉树遍历的递归实现

 

目录

树 

树的学术名词

树的种类

 二叉树的遍历

算法实现

遍历命名

二叉树的中序遍历

二叉树的后序遍历

二叉树的后序遍历迭代算法

 二叉树的前序遍历

二叉树的前序遍历迭代算法

 

---

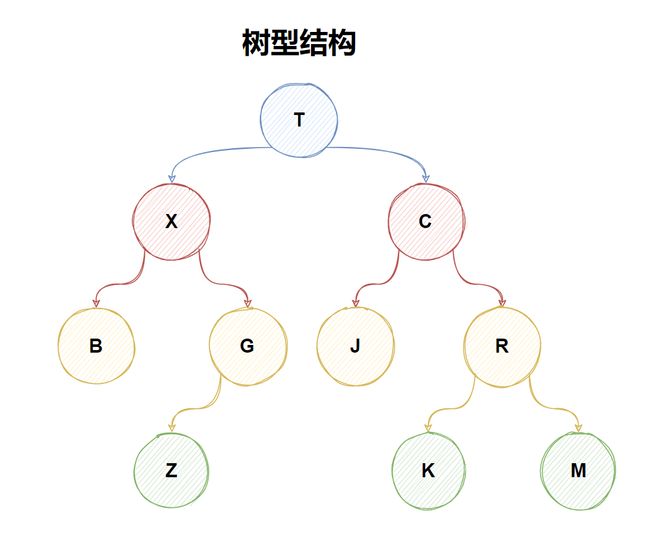
树 

树是一种非线性的数据结构，它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

• 每个节点有零个或多个子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树

树的学术名词

• 根节点(root): 树的最上层的节点，任何非空的树都有一个节点
• 路径(path): 从起始节点到终止节点经历过的边
• 父亲(parent)：除了根节点，每个节点的上一层边连接的节点就是它的父亲(节点)
• 孩子(children): 每个节点由边指向的下一层节点
• 兄弟(siblings): 同一个父亲并且处在同一层的节点
• 子树(subtree): 每个节点包含它所有的后代组成的子树
• 叶子节点(leaf node): 没有孩子的节点成为叶子节点

树的种类

无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树；

有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；

二叉树：每个节点最多含有两个子树的树称为二叉树；

满二叉树：所有节点均含有两个子树的树被称为满二叉树；

完全二叉树：除最后一层外，所有层都是满节点，且最后一层缺右边连续节点的二叉树称为完全二叉树；

哈夫曼树（最优二叉树）：带权路径最短的二叉树称为哈夫曼树或最优二叉树。

 二叉树的遍历

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问

访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础

算法实现

从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作：

• 访问节点的本身（Node）
• 遍历该节点的左子树（L）
• 遍历该节点的右子树 （R）

以上三种操作拥有六种执行顺序：

NLR，LNR，LRN，NRL，RNL，RLN。

但是注意前三种次序和后三种次序对称，所以我们只学习前三种次序

遍历命名

根据访问结点操作发生位置命名：

• NLR：二叉树的前序遍历(Preorder Traversal 亦称(先序遍历))

  访问根结点的操作发生在遍历其左右子树之前

• LNR：二叉树的中序遍历(Inorder Traversal)

  访问根结点的操作发生在遍历其左右子树之中(间)

• LRN：二叉树的后序遍历(Postorder Traversal)

  访问根结点的操作发生在遍历其左右子树之后

   

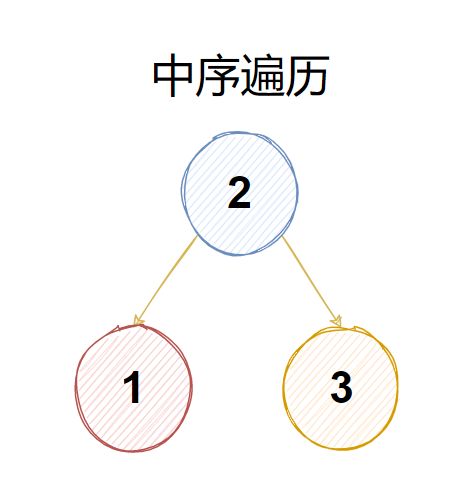
二叉树的中序遍历

若二叉树非空，则依次执行如下操作：

1. 遍历左子树
2. 访问根节点
3. 遍历右子树

# Definition for a binary tree node.
# class TreeNode:
#   def __init__(self, val=0, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right
class Solution:
  def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    # 左 根 右
    def inorder(root : TreeNode):
      if not root:
        return
      
      inorder(root.left)
      res.append(root.val)
      inorder(root.right)




    res = list()
    inorder(root)
    return res

 

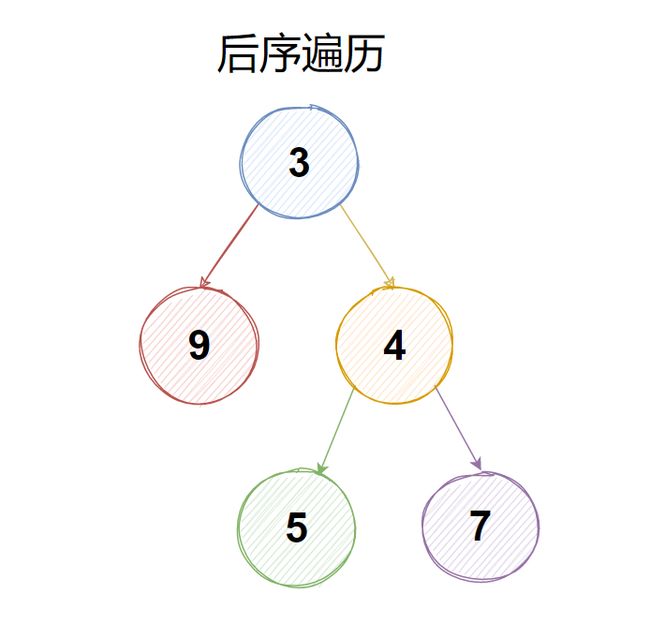
二叉树的后序遍历

若二叉树非空，则依次执行如下操作：

1. 遍历左子树
2. 遍历右子树
3. 访问根节点

# Definition for a binary tree node.
# class TreeNode:
#   def __init__(self, val=0, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right
class Solution:
  def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    # 后序遍历的顺序：左 右 根
    def postorder(root : TreeNode):
      if not root:
        return
      
      postorder(root.left)
      postorder(root.right)
      res.append(root.val)




    res = list()
    postorder(root)
    return res

二叉树的后序遍历迭代算法

1. 建立一个栈，用来存储节点。

2. 根据根右左的顺序将节点依次压入栈中，在压入栈中的同时，按照顺序把节点里的元素依次压入栈中。输出完毕之后按照顺序弹栈。

3. 将答案数组进行反转，得到左右根顺序的数组

4. 输出答案

   

期望结果:[9,5,7,4,3]

# Definition for a binary tree node.
# class TreeNode:
#   def __init__(self, val=0, left=None, right=None):
#     self.val = val
#     self.left = left
#     self.right = right
class Solution:
  def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    res = []
    stack = []
    while root or stack:
      while root:
        res.append(root.val)
        stack.append(root)
        root = root.right
      root = stack.pop().left #根 右 左的顺序


    res.reverse() 
    return res

 二叉树的前序遍历

若二叉树非空，则依次执行如下操作：

1. 访问根节点

2. 遍历左子树

3. 遍历右子树

   

    

   class Solution:
     def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
       # 创建一个集合存储数据
       res = []
       def preorder(root:TreeNode):
         # 判断root是否有值
         if not root:
           return
         else:
           # 获取根节点
           res.append(root.val)
           # 获取左节点
           preorder(root.left)
           # 获取右节点
           preorder(root.right)
       preorder(root)
       return res
   

   二叉树的前序遍历迭代算法

4. 建立一个栈，用来存储节点。
5. 根据左右根的顺序将节点依次压入栈中，在压入栈中的同时，按照顺序把节点里的元素依次压入栈中。输出完毕之后按照顺序弹栈。
6. 输出答案。

class Solution:
  def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    # 创建res存储结果
    res = []
    stack = [] # 存储分支节点
    # 只要root有数据 或者stack的数据
    while root or stack:
      # 只要root有数据,第一轮循环把左节点搞定
      while root:
        res.append(root.val)
        stack.append(root)
        # 获取左节点
        root = root.left
      # 取出右节点，遍历
      root = stack.pop().right
    return res