递归、迭代与循环

一、递归（以斐波那契数列递归方法为例）

1.递归定义

在定义一个过程或函数时，出现直接或者间接调用自己的成分，称之为递归。在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。简单来说，递归表现为函数调用函数本身。
在知乎看到一个比喻递归的例子，个人觉得非常形象，大家看一下：

递归最恰当的比喻，就是查词典。我们使用的词典，本身就是递归，为了解释一个词，需要使用更多的词。当你查一个词，发现这个词的解释中某个词仍然不懂，于是你开始查这第二个词，可惜，第二个词里仍然有不懂的词，于是查第三个词，这样查下去，直到有一个词的解释是你完全能看懂的，那么递归走到了尽头，然后你开始后退，逐个明白之前查过的每一个词，最终，你明白了最开始那个词的意思。

递归的特点:

• 自身调用：原问题可以分解为子问题，子问题和原问题的求解方法是一致的，即都是调用自身的同一个函数。
• 终止条件：递归必须有一个终止的条件，即不能无限循环地调用本身。

（1）若直接调用自己，称为直接递归；若间接调用自己，则称为间接递归，示意图如下。

（2）如果一个递归函数中递归调用语句是最后一条执行语句，则称这种递归调用为尾递归，如上面的求n！（直接递归）。

2.使用递归

何时使用递归

（1）定义是递归的。有许多数学公式、数列等的定义是递归的，如上面的求n！（直接递归），二叉树的定义也是递归的。

（2）数据结构是递归的，如单链表

（3）问题的求解方法是递归的，如最著名的Hanoi塔问题。

如何使用递归

为了更好的利用递归求解问题，我们现在通过求n! 递归算法认识递归结构，并抽象出递归模型。

首先建立递归模型，一般地，一个递归模型是由递归出口（递归条件）和递归体两部分组成。**递归出口确定递归到何时结束；递归体确定递归求解时的递推关系。**如此，我们类推出递归出口和递归体的一般格式：
1）递归出口，一般格式如下：f(s1) = m1。

其中，s1与m1均为常量，有些递归问题可能有几个递归出口。如求n!，fun(1)=1就是f(s1) = m1。

2）递归体，一般格式如下：f(sn)=g(f(si)，f(si+1)，…，f(sn-1)，cj，cj+1，…，cm)。

其中，g是一个非递归函数（一般为fun(n)的前几步fun(n-1）、fun(n-2)……），cj，cj+1，…，cm为常量。如求n!，fun(n)=n*fun(n-1)（n>1）就是f(sn)=g(f(si)，f(si+1)，…，f(sn-1)，cj，cj+1，…，cm)的反应，只是“cj，cj+1，…，cm”均为0，
“f(si)，f(si+1)，…，f(sn-1)”中仅存在一个fun(n-1)，此外f(sn)为f(n)，g为n*fun(n-1) 。

递归思路：
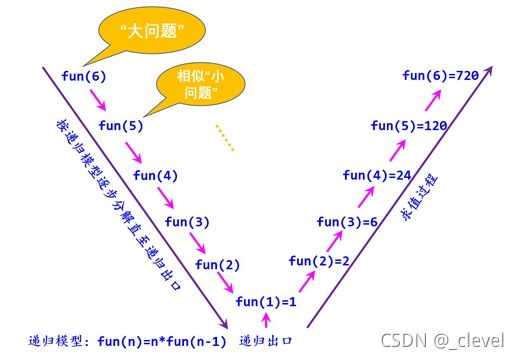
递归的思路就是：把一个不能或不好直接求解的“大问题”转化成一个或几个与“大问题”相似的“小问题”来解决；再把这些“小问题”进一步分解成更小的相似的“小问题”来解决。我们现在以求6！为例，看一下递归问题的求解过程。

3.递归实例（以斐波那契数列为例）

#include 
#include 
using namespace std;

int fib(int n)
{

    if(n==1)
    {
        cout<<"f(1)"<<endl;
        return 1;
    }
    else if(n==2)
    {
        cout<<"f(2)"<<endl;
        return 1;
    }
    else {
        cout<<"f("<<n<<"):"<<"f("<<n-1<<")+"<<"f("<<n-2<<")"<<endl;
        return fib(n-1)+fib(n-2);
    }
}
int main()
{
    
    int num = fib(7);
    cout<< num<<endl;;
    
    system("pause");
    return 0;
}

运行结果：


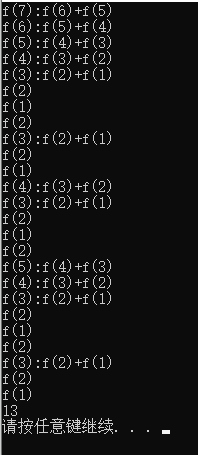
这里主要是为了说明，递归调用过程自身函数栈调用的情况，程序结果表明，递归先一直调用遇到的第一个递归函数，之后返回再调用下一个，有点类似二叉树的前序遍历，中左右 的顺序。递归树如下图

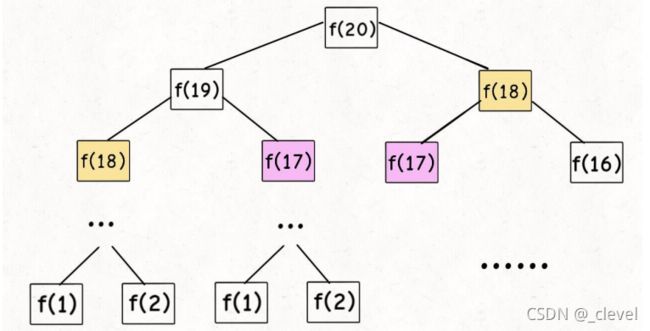
递归算法的时间复杂度计算：⼦问题个数$\times$解决⼀个⼦问题需要的时间。
⼦问题个数： 即递归树中节点的总数，显然⼆叉树节点总数为指数级别，所以⼦问题个数为 O(2ⁿ)。
解决⼀个⼦问题的时间： 在本算法中，没有循环，只有 f(n - 1) + f(n - 2) ⼀ 个加法操作，时间为 O(1)。
所以，这个算法的时间复杂度为 == O(2ⁿ) ==，指数级别，爆炸。
可以看出，上面的递归树，从f(18)就重复计算，越是下面的层，重复计算次数越多，增加了巨大的时间复杂度，这类似与动态规划中的 重叠子问题。

⼀般使⽤⼀个数组充当这个「备忘录」，也可以使⽤哈希表（字典）

现在递归算法的时间复杂度就是O(n)

4.递归与栈

函数调用通过栈来实现，当调用函数时，系统会再开辟一个栈空间去调用函数操作，调用完之后再返回原程序地址。
栈，是一种数据结构，是限定仅在表尾进行插入或删除操作的线性表，数据总是先进后出。
一个进程使用的内存都可以按照功能大致分为代码区、数据区、堆区和栈区4个部分，内存的栈区实际上指的就是系统栈，系统栈由系统自动维护，它用于实现高级语言中函数的调用（即栈用于维护函数调用的上下文，离开了栈函数调用就没法实现）。
递归函数调用经常是嵌套的，在同一时刻，栈中会有多个函数的信息。每个未完成运行的函数占用一个独立的连续区域，称作栈帧，即系统栈又分为若干个栈帧，栈帧记录在栈上面，栈上保持了N个栈帧的实体。每个函数执行的同时都会创建一个栈帧，用于存储局部变量表、操作数栈、动态链接、函数出口等信息，每一个函数从调用直至执行完毕的过程，就对应着一个栈帧在虚拟机中入栈到出栈的过程，且当前正在运行的函数的栈帧总是在栈顶，体现先进后出的特点！

//一个求和的例子
public int sum(int n) {
    if (n <= 1) {
        return 1;
    } 
    return sum(n - 1) + n; 
}

5.递归与迭代

（1）递归常被用来描述以自相似方法重复事物的过程，形象的说就是A调用A，在函数的定义中直观的表现为：直接或间接调用函数自身；（2）迭代则是重复反馈过程的活动，是利用已知的变量值，根据递推公式不断将上一次迭代的结果作为下一次迭代的初始值，从而得到变量新值的一种编程思想，其形象的说是A重复调用B，在函数内直观的表现为：某段代码实现循环。接下来就以著名的斐波那契数列来举例看递归和迭代的不同实现方式，斐波那契数列：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。

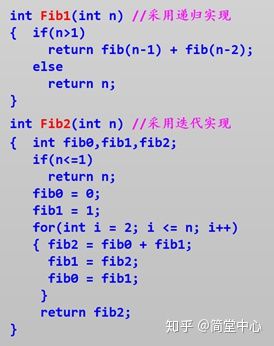
6.迭代与循环

迭代与循环又该如何区分呢？迭代是利用循环语句实现重复反馈过程的活动，而循环，单纯是实现反复执行某个功能，以减少重复书写。那么看到包含循环语句的代码时，该如何判断其是否是迭代呢？迭代时，循环代码中参与运算的变量同时是保存结果的变量，当前保存的结果作为下一次循环计算的初始值。

递归转化为非递归（迭代）

1. 尾递归算法转非递归

通常尾递归算法可以通过循环或者迭代方式转换为等价的非递归算法，如求n！

2. 非尾递归算法转非递归

非尾递归算法，在理解递归调用实现过程的基础上，可以用栈模拟递归执行过程，从而将其转换为等价的非递归算法。例如二叉树的后序遍历，可以使用递归算法实现，也可以通过栈实现后序非递归算法，算法具体实现将在二叉树遍历时讲解。

参考：https://zhuanlan.zhihu.com/p/343467573