逆波兰表达式（c++）

为什么使用逆波兰表达式

很多人会有疑问，中缀表达式（即2+3*2-3的形式）更直观，也更符合我们人类的视觉效果，为什么要使用不美观，而且很需要我们转变之后才能看懂的逆波兰表达式。

​ 因为对于计算机而言，逆波兰表达式是最简便也是方便计算机计算的一种表达形式。想要知道为什么这种形式比较符合计算机处理的小伙伴可以了解一些计算机组成原理的相关知识。

实现

• 首先我们需要将中缀表达式转换为后缀表达式。

比如：2+3*2-2 转成后缀表达式之后为2 3 2 * + 2 -

​ （2-3）*3-5 —> 2 3 - 3 * 5 -

本质：是将运算符提到数字的后面，拿2+32-2举例：我们要先算3 * 2 ，就把放到3 2 的后面，即3 2 * 然后将3 2 *看作一个整体然后需要与2进行加法运算，将+号放到3 2 *和2的后面，即2 3 2 * +。其他以此类推。

​ 在这个过程中要遵循左优先原则 拿2+3*2-2举例，在我们计算完3 * 2之后，我们可以计算减法也可以计算加法，但是遵循 左优先原则

我们要先算加法。

	编程实现思想：使用一个栈来存储为确实的运算符，将算数表达式从左往右扫描，遇到运算符加入栈中，这又可以分成以下几种情况：

• 当栈中为空时，直接入栈，

• 当栈不为空并且遇到“（”时，直接入栈

• 当栈不为空，栈顶也是运算符时，如果当前运算符大于栈顶的优先级时，直接入栈；如果时小于或者等于时，将栈顶元素出栈，直到当前运算符大于栈顶元素或者栈空或者遇到“(”；然后将当前运算符入栈

• 如果当前元素是“）”时，将栈顶元素出栈，直到遇到“（”，然后“）”不用入栈

• 如何将后缀表达式通过计算得到结果

  ​ 拿2 3 2 * + 2 -举例：将算数表达式从左往右扫描遇到数字直接入栈，比如2 3 2直接入栈；当遇到运算符时将两个栈顶元素出栈，然后进行运算，将计算的结果入栈，以此类推，最后栈中只剩一个元素，即时运算的结果。

代码实现（直接将中缀表达得到结果）

​ 这需要准备两个栈，一个用于存放未确定的运算符，一个用于存放数字

实现的思想：将算法表达式从左往右扫描，如果遇到数字直接将数字入数字栈，遇到算术运算符或者括号进行以下操作

• 当运算符栈中为空时，直接入运算符栈，

• 当运算符栈不为空并且遇到“（”时，直接入运算符栈

• 当运算符栈不为空，运算符栈顶也是运算符时，如果当前运算符大于栈顶的优先级时，直接入运算符栈；如果时小于或者等于时，将运算符栈顶元素出栈，并将数字栈的两个栈顶元素出栈，并进行计算，将计算结果入数字栈，直到当前运算符大于栈顶元素或者栈空或者遇到“(”；然后将当前运算符入运算符栈

• 如果当前元素是“）”时，将运算符栈顶元素出栈，直到遇到“（”，然后“）”不用入运算符栈

  其实就是将前面两个方法整合成一个算法。

  以下是自己定义栈来实现的，也可以通过c++中自带的栈来实现

代码：

#include
#include
#include
using namespace std;
#define MaxSize 10
typedef char Elemtype;
typedef int Elemtype1;
typedef struct Stack{
	int top;
	Elemtype data[MaxSize];	
}Stack;
//初始化栈
void InitStack(Stack &s){
	s.top = -1;
} 
//判断是否未空 
bool IsEmpty(Stack s){
	return s.top == -1 ? true:false;
}
//进栈
void Push(Stack &s,Elemtype ch){
	if(s.top == MaxSize - 1){
		cout<<"栈满";
		return; 
	}
	s.data[++s.top] = ch;
} 
//出栈
bool Pop(Stack &s,Elemtype &x){
	if(IsEmpty(s)){
		return false;
	}
	x = s.data[s.top--];
	return true;
} 
//查看栈顶元素
bool getTop(Stack s,Elemtype &x){
	if(IsEmpty(s)){
		return false;
	}
	x = s.data[s.top];
	return true;
} 

typedef struct Stack1{
	int top;
	Elemtype1 data[MaxSize];	
}Stack1;
//初始化栈
void InitStack1(Stack1 &s){
	s.top = -1;
} 
//判断是否未空 
bool IsEmpty1(Stack1 s){
	return s.top == -1 ? true:false;
}
//进栈
void Push1(Stack1 &s,Elemtype1 ch){
	if(s.top == MaxSize - 1){
		cout<<"栈满";
		return; 
	}
	s.data[++s.top] = ch;
} 
//出栈
bool Pop1(Stack1 &s,Elemtype1 &x){
	if(IsEmpty1(s)){
		return false;
	}
	x = s.data[s.top--];
	return true;
} 
//查看栈顶元素
bool getTop1(Stack1 s,Elemtype1 &x){
	if(IsEmpty1(s)){
		return false;
	}
	x = s.data[s.top];
	return true;
} 


//将加减乘除转换为相应的数字 
//加减用1表示，乘除用2来表示
int getNum(char ch){
	if(ch == '+' || ch == '-'){
		return 1;
	}else {
		return 2;
	}
}
//计算运算符的优先级
//ch1比ch2高则返回1，低则返回-1 等于返回0 
int getPriority(char ch1,char ch2){
	int c1 = getNum(ch1);
	int c2 = getNum(ch2);
	return c1 - c2;
}

//加减乘除运算
int getCounter(int num1,int num2,char ch){
	if(ch == '+'){
		return num1 + num2;
	}else if(ch == '-'){
		return num1 - num2;
	}else if(ch == '*'){
		return num1*num2;
	}else{
		return num1/num2;
	}
} 
 
//逆波兰计算算术表达式
int counter(string str){
	Stack s;//用于存储不确定的运算符 
	Stack1 t;//用于存储不确定的数字
	InitStack(s);
	InitStack1(t);
	char x = ' ';//用于保存查看的栈顶元素 (运算符)
	char y = ' ';//用于保存出栈的元素（运算符） 
	int i = 0;//记录字符串的下标 
	char c = str[i];//存放字符串中的字符 
	int num1,num2;
	while(c != '\0'){
			if(c == '+' || c == '-' || c == '*' || c == '/'){
				if(IsEmpty(s)){
					Push(s,c);
				}else{//不为空，比较栈顶的运算符优先级 ，大于则直接入栈，
				//否则弹出栈顶元素进行计算后入栈
				getTop(s,x);
				if(x == '(' || x == '[' || x == '{'){
					Push(s,c);		
				}else{
					while(getPriority(c,x) != 1 && !IsEmpty(s)){
						Pop(s,y);
						Pop1(t,num2);
						Pop1(t,num1);
						Push1(t,getCounter(num1,num2,y));
						getTop(s,x);
						if(x == '(' || x == '[' || x == '{'){
							break;
						}
					} 
					Push(s,c);
				}
				}
			}else if(c == '(' || c == '[' || c == '{'){
				Push(s,c);
			}else if(c == ')'|| c == ']'|| c == '}'){
				Pop(s,y);
					do{
						Pop1(t,num2);
						Pop1(t,num1);
						Push1(t,getCounter(num1,num2,y));
						Pop(s,y);
						if(y == '(' || y == '[' || y =='{'){
							break;
						}
					}while(!IsEmpty(s));
			}else{
				int j = i + 1;
				while(str[j] != '\0' && str[j] != '+' &&str[j] != '-'&&str[j] != '*'&&str[j] != '/'){
					if(str[j] == ')'|| str[j] == ']'|| str[j] == '}'){
						break;
					}
					j++;
				}
				string st = str.substr(i,j);
				int z = atoi(st.c_str());
				Push1(t,z);
				i = j - 1;
			}
		i++;
		c = str[i];
	}
	//最后将存放运算符和数字的元素弹出，并进行计算
	Pop(s,y);
	Pop1(t,num2);
	Pop1(t,num1);
	Push1(t,getCounter(num1,num2,y));
	int g;
	Pop1(t,g);
	return g; 
} 
int main(){
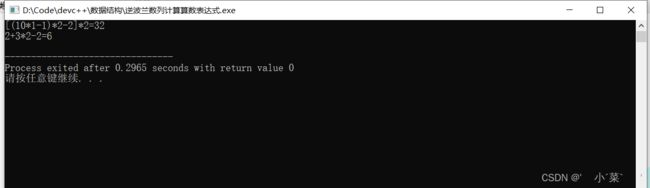
	string str = "[(10*1-1)*2-2]*2";//32
	cout<<"[(10*1-1)*2-2]*2="<