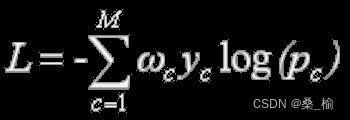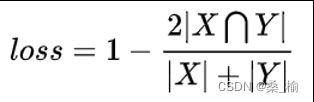图像分割场景中四种常见的损失函数（附代码）

一 交叉熵损失

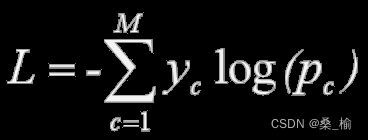
优点：交叉熵损失可以用在大多数语义分割场景中
缺点：对于只分割前景和背景的时候，当前景像素的数量远远小于背景像素的数量的时候，即y=0的数量远远大于y=1的数量，损失函数中的y=0成分就会占主导，使得模型严重偏向背景，导致效果不好

加权交叉熵

BCELoss

基本等价于二分类交叉熵，通常接sigmoid激活函数的输出

二 Focal Loss

源自目标检测（RetinaNet），是对标准交叉熵的一种改进，主要解决难易样本数量不平衡的问题，当正负样本数量不平衡时，可以通过在交叉熵中引入参数进行调节。

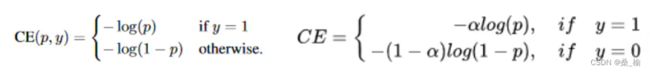
虽然以上公式平衡了正负样本的数量，但是，目标检测中大量的候选目标都是易分样本，这样样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。
因此，Focalloss认为易分样本对模型的提升效果非常小，模型应该主要关注那些难分样本。

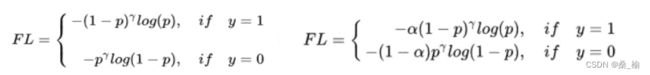
**参数P：**当p趋近于0的时候，调制因子1-p接近于1，损失不受影响，当p趋近于1的时候，1-p接近0，从而减小易分样本对总loss的损失
**参数gama：**当gama=0时，Focal就是传统的交叉熵，当它等于2时，易分样本loss就会很小，难分就会很大。

class FocalLoss(nn.Module):
    def __init__(self, alpha=0.25, gamma=2, size_average=True, ignore_index=255):
        super(FocalLoss, self).__init__()
        self.alpha = alpha
        self.gamma = gamma
        self.ignore_index = ignore_index
        self.size_average = size_average # 对batch里面的数据取均值/求和

    def forward(self, inputs, targets):
        ce_loss = F.cross_entropy(inputs, targets, ignore_index=self.ignore_index)
        pt = torch.exp(-ce_loss)
        focal_loss = self.alpha * (1-pt)**self.gamma * ce_loss
        if self.size_average:
            return focal_loss.mean()
        else:
            return focal_loss.sum()

三 Dice系数

是用来度量集合相似度的函数，通常用于计算两个样本之间的像素相似度

TP是真实为1预测也为1
FN是真实为1预测为0
FP是真实为0预测为1
TN是真实为0预测为0
DiceLoss适用于样本极度不平衡的情况，一般情况下使用DiceLoss会对反向传播不利，使得训练不稳定。

class DiceLoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(DiceLoss, self).__init__()
        
        self.size_average = size_average
 
    def forward(self, probs, labels):
        """
        probs = [1, 12, 360, 480]
        targets = [1, 12, 360, 480]
        """
        targets = make_one_hot(labels.unsqueeze(0), 12)
        num = targets.size(1) # num=12
        smooth = 1

        m1 = probs.view(num, -1)   # m1 = 12, 172800
        
        m2 = targets.view(num, -1) # m2 = 12, 172800

        intersection = (m1 * m2)   # intersection = 12，172800

        score = 2. * (intersection.sum(1) + smooth) / (m1.sum(1) + m2.sum(1) + smooth)
    
        dice_loss = 1 - score.sum() / num
        
        if self.size_average:
            return dice_loss.mean()
        else:
            return dice_loss.sum()

其中将mask变成独热编码的函数：

def make_one_hot(input, num_classes):
    """
    input.shape = [1, 1, 360, 480]
    num_classes = 12
    output.shape = [1, 12, 360, 480]
    """
    shape = np.array(input.shape) # shape = [1, 1, 352, 480]
    shape[1] = num_classes # shape = [1, 12, 352, 480]
    shape = tuple(shape) 
    result = torch.zeros(shape)
    result = result.scatter_(1, input.cpu(), 1) # scatter_直接在原始Tensor上做修改

    return result

scatter_()函数：scatter()和scatter_()的作用是一样的。scatter()不会直接修改原来的Tensor，而scatter_()会直接修改原来的Tensor
scatter(dim, index, src)：
dim：沿着哪个维度进行索引
index：元素索引
src：源元素，可以是一个标量或一个张量

官方文档举例：三维向量

self[index[i][j][k]][j][k] = src[i][j][k]   # if dim == 0

self[i][index[i][j][k]][k] = src[i][j][k]   # if dim == 1

self[i][j][index[i][j][k]] = src[i][j][k]   # if dim == 2

mask_batch = mask_tensor.unsqueeze(0).unsqueeze(0)
mask_one_hot = make_one_hot(mask_batch, 12)

print("原标签尺寸:\n", mask_tensor.shape, '\n')
print("先增加一维batchsize，再增加一维通道后标签尺寸:\n", mask_batch.shape, '\n')
print("经过独热编码后尺寸:\n", mask_one_hot.shape, '\n')
print("经过独热编码后某一维标签尺寸:\n", mask_one_hot[:,1,:,:], '\n')

原标签尺寸:
torch.Size([360, 480])
先增加一维batchsize，再增加一维通道后标签尺寸:
torch.Size([1, 1, 360, 480])
经过独热编码后尺寸:
torch.Size([1, 12, 360, 480])
经过独热编码后某一维标签尺寸:
tensor([[[1., 1., 1., …, 0., 0., 0.],
[1., 1., 1., …, 0., 0., 0.],
[1., 1., 1., …, 0., 0., 0.],
…,
[0., 0., 0., …, 0., 0., 0.],
[0., 0., 0., …, 0., 0., 0.],
[0., 0., 0., …, 0., 0., 0.]]])

DiceLoss

IOULOSS

四 Jaccard系数

定义为A与B交集的大小与AyuB并集的大小的比值

五 Tversky系数

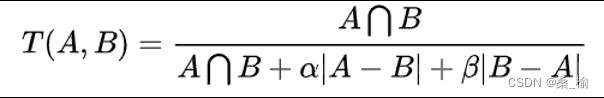
当alpha和bata都是0.5时，这个就是Dice系数，当都为1时，就是Jaccard系数

六 Lovasz-SoftmaxLoss（有难度）

对jaccard进行扩展，表现更好

class LovaszSoftmax(nn.Module):
    def __init__(self, ignore=None, size_average=True):
        super(LovaszSoftmax, self).__init__()
        """
        Multi-class Lovasz-Softmax loss
          probas: [B, C, H, W] Variable, class probabilities at each prediction (between 0 and 1).
                  Interpreted as binary (sigmoid) output with outputs of size [B, H, W].
          labels: [B, H, W] Tensor, ground truth labels (between 0 and C - 1)
          ignore: void class labels
        """
        """
        probas.shape = [1, 3, 4, 4]
        labels.shape = [1, 4, 4]
        """
        
        self.size_average = size_average
        self.ignore = ignore
 
    def forward(self, probas, labels):
        loss = lovasz_softmax_flat(*flatten_probas(probas, labels, self.ignore))
        return loss


def flatten_probas(probas, labels, ignore=None):
    """
    Flattens predictions in the batch
    """
    B, C, H, W = probas.size() # 1, 3, 4, 4
    probas = probas.permute(0, 2, 3, 1).contiguous().view(-1, C)  # 1, 4, 4, 3 --> 16, 3
    labels = labels.view(-1) # 16

    if ignore is None:
        return probas, labels
    valid = (labels != ignore)
    vprobas = probas[valid.nonzero().squeeze()]
    vlabels = labels[valid]
    return vprobas, vlabels


def lovasz_softmax_flat(probas, labels):
    """
    Multi-class Lovasz-Softmax loss
      probas: [P, C] Variable, class probabilities at each prediction (between 0 and 1)
      labels: [P] Tensor, ground truth labels (between 0 and C - 1)
    """
    """
    probas.shape = [16, 3]
    labels.shape = [16]
    labels = [1, 1, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 1, 1, 0, 1]
    """
    C = probas.size(1) # C = 3
    losses = []
    class_to_sum = list(range(C)) # class_to_sum = [0, 1, 2]
    for c in class_to_sum:
        fg = (labels == c).float()  # δ
        class_pred = probas[:, c]

        """
        c = 0:
        fg = [0., 0., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 0., 0., 1., 0.]
        class_pred = [0.6565, 0.8674, 0.8831, 0.4174, 0.4845, 0.1666, 0.2379, 0.4416, 0.5015,
        0.9657, 0.4523, 0.2172, 0.3103, 0.5980, 0.7919, 0.4523]
        
        c = 1
        fg = [1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 1.]
        class_pred = [0.8110, 0.4605, 0.9819, 0.3185, 0.7950, 0.1819, 0.7492, 0.7690, 0.8270,
        0.3137, 0.0826, 0.8931, 0.9237, 0.3156, 0.6388, 0.6351]
        
        c = 2
        fg = [0., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 0., 0., 0., 0.]
        class_pred = [0.0658, 0.8870, 0.9484, 0.2572, 0.4305, 0.2031, 0.3526, 0.3824, 0.4131,
        0.4258, 0.0298, 0.3857, 0.8182, 0.7671, 0.5974, 0.1790]
        """
        errors = (Variable(fg) - class_pred).abs()   # m
        errors_sorted, perm = torch.sort(errors, 0, descending=True)  # π
        perm = perm.data
        fg_sorted = fg[perm]

        """
        c = 0:
        errors = [0.6565, 0.8674, 0.8831, 0.4174, 0.4845, 0.8334, 0.2379, 0.4416, 0.5015,
                  0.0343, 0.4523, 0.2172, 0.3103, 0.5980, 0.2081, 0.4523]
                  
        errors_sorted = [0.8831, 0.8674, 0.8334, 0.6565, 0.5980, 0.5015, 0.4845, 0.4523, 0.4523,
                         0.4416, 0.4174, 0.3103, 0.2379, 0.2172, 0.2081, 0.0343]
                         
        perm = [ 2,  1,  5,  0, 13,  8,  4, 10, 15,  7,  3, 12,  6, 11, 14,  9]
        
        fg_sorted = [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1.]
        """
        
        losses.append(torch.dot(errors_sorted, Variable(lovasz_grad(fg_sorted)))) # torch.dot()：一维向量对应位置相乘再相加
    return mean(losses)


def lovasz_grad(gt_sorted):
    p = len(gt_sorted) # p = 16
    gts = gt_sorted.sum() # 4
    intersection = gts - gt_sorted.float().cumsum(0)
    union = gts + (1 - gt_sorted).float().cumsum(0)
    jaccard = 1. - intersection / union
    if p > 1:  # cover 1-pixel case
        jaccard[1:p] = jaccard[1:p] - jaccard[0:-1]
    return jaccard


def isnan(x):
    return x != x


def mean(l, ignore_nan=False, empty=0):
    """
    nanmean compatible with generators.
    """
    l = iter(l)
    if ignore_nan:
        l = ifilterfalse(isnan, l)
    try:
        n = 1
        acc = next(l)
    except StopIteration:
        if empty == 'raise':
            raise ValueError('Empty mean')
        return empty
    for n, v in enumerate(l, 2):
        acc += v
    if n == 1:
        return acc
    return acc / n

总结

BCELoss + DiceLoss ：将两者进行组合，在数据较为均衡情况下有所改善，但是在数据极度不平衡的情况下交叉熵会在迭代几个Epoch之后远小于DiceLoss，这个组合Loss会退化为DiceLoss
Focal Loss + DiceLoss：论文提出来解决小器官分割问题