opencv基础59-霍夫变换原理讲解及示例-cv2.HoughLines()-＞(直线，圆形检测)

霍夫变换是一种在图像中寻找直线、圆形以及其他简单形状的方法。霍夫变换采用类似于投票的方式来获取当前图像内的形状集合，该变换由 Paul Hough（霍夫）于 1962 年首次提出。
最初的霍夫变换只能用于检测直线，经过发展后，霍夫变换不仅能够识别直线，还能识别其他简单的图形结构，常见的有圆、椭圆等。

霍夫变换应用场景

霍夫变换在计算机视觉和图像处理领域中具有广泛的应用，主要用于检测图像中的几何形状，特别是直线和圆。以下是一些霍夫变换的应用场景：

1. 直线检测： 霍夫变换可用于检测图像中的直线，无论这些直线是水平、垂直还是倾斜的。应用场景包括道路标线检测、图像中的边缘检测、图像中的线条检测等。

2. 圆检测： 圆霍夫变换可用于检测图像中的圆形，例如在图像中识别圆形物体、检测圆形物体的轮廓等。

3. 椭圆检测： 扩展的霍夫变换可以用于检测图像中的椭圆，应用场景包括眼球检测、图像中的椭圆轮廓识别等。

4. 直线和圆的参数估计： 霍夫变换可以用于估计图像中的直线和圆的参数，例如直线的斜率和截距，圆的半径和圆心位置。

5. 图像分析与特征提取： 霍夫变换可以用于分析图像中的几何特征，例如检测道路交叉口、分析图像中的纹理等。

6. 形状检测与识别： 霍夫变换可以用于识别特定形状的对象，例如在工业检测中检测零件的缺陷。

7. 图像中的直线和轮廓重建： 通过霍夫变换，可以检测到图像中的直线和轮廓，然后利用这些信息进行图像重建。

8. 图像配准与拼接： 霍夫变换可用于在不同视角下或不同图像之间检测共享几何结构，从而实现图像配准和拼接。

9. 数字图像处理和计算机视觉教学： 霍夫变换是一个重要的教学工具，用于讲解图像处理中的几何形状检测原理。

霍夫直线变换

OpenCV 提供了函数 cv2.HoughLines()和函数 cv2.HoughLinesP()用来实现霍夫直线变换。
本节首先介绍霍夫变换的基本原理，然后分别介绍这两个函数的基本使用方法。

霍夫变换原理

为了方便说明问题，先以我们熟悉的笛卡儿¹ 坐标系（与笛卡儿空间对应）为例来说明霍夫变换的基本原理。与笛卡儿坐标系对应，我们构造一个霍夫坐标系（对应于霍夫空间）。

在霍夫坐标系中，横坐标采用笛卡儿坐标系中直线的斜率 k，纵坐标使用笛卡儿坐标系中直线的截距 b。

首先，我们观察笛卡儿空间中的一条直线在霍夫空间内的映射情况。
例如，在图 16-1 中，左图是笛卡儿 x-y 坐标系（笛卡儿空间），右图是霍夫 k-b 坐标系（霍夫空间）。在笛卡儿空间中，存在着一条直线 = 0 + 0，该直线的截距0是已知的常量，截距0也是已知的常量。
将该直线映射到霍夫空间内，找到已知的点(0, 0)，即完成映射。

从上述分析中可知，笛卡儿空间内的一条直线，其斜率为 k，截距为 b，映射到霍夫空间内成为一个点(k, b)。或者，可以这样理解，霍夫空间内的一个点(0, 0)，映射到笛卡儿空间，就是一条直线 = 0 + 0。

这里，我们用“映射”这个词表达不同的空间（坐标系）之间的对应关系，也可以表述为“确定”。例如，上述关系可以表述为：

• 笛卡儿空间内的一条直线确定了霍夫空间内的一个点。
• 霍夫空间内的一个点确定了笛卡儿空间内的一条直线。

接下来，观察笛卡儿空间中的一个点在霍夫空间内的映射情况。如图 16-2 所示，在笛卡儿空间内存在一个点(0, 0)，通过该点的直线可以表示为0 = 0 + 。其中，(0, 0)是已知的常量，(k, b)是变量。

对于表达式0 = 0 + ，通过算术运算的左右移项，可以表示为 = −0 + 0。将点(0, 0)映射到霍夫空间时，可以认为对应的直线斜率为−0，截距为0，即 = −0 + 0，如图 16-2 中右图的直线所示。

从上述分析可知：

• 笛卡儿空间内的点(0, 0)映射到霍夫空间，就是直线 = −0 + 0。
• 霍夫空间内的直线 = −0 + 0映射到笛卡儿空间，就是点(0, 0)。

下面我们看看笛卡儿空间中的两个点映射到霍夫空间的情况。例如，在图 16-3 中，左图的笛卡儿空间中存在着两个点(0, 0)、(1, 1)，分析这两个点映射到霍夫空间的情况。

为了方便理解，我们从不同的角度分析笛卡儿空间中这两个点到霍夫空间的映射情况。

• 角度 1：笛卡儿空间的一个点会映射为霍夫空间的一条线。
  在笛卡儿空间内，存在着任意两个点(0, 0)、(1, 1)。在霍夫空间中，这两个点对应着两
  条不同的直线。当然，通过分析可知，一条直线是 = −0 + 0，另外一条直线是 = −1 + 1。

• 角度 2：笛卡儿空间的一条线会映射为霍夫空间的一个点在笛卡儿空间内，存在着任意两个点(0, 0)、(1, 1)。这两个点一定能够用一条直线连接，将连接它们的直线标记为 = 1 + 1，则该直线的截距和斜率是(k1, b1)。也就是说，该直线在霍夫空间内映射为点(k1, b1)。

从上述分析可知：

• 笛卡儿空间内的两个点会映射为霍夫空间内两条相交于(k1, b1)的直线。
• 这两个点对应的直线会映射为霍夫空间内的点(k1, b1)。

换句话说，角度 1 决定了线条的数量，角度 2 决定了两条线相交的点。

这说明，如果在笛卡儿空间内有两个点 A、B，它们能够连成一条直线 = 1 + 1，那么在霍夫空间中的点(k1, b1)上会有两条直线，分别对应着笛卡儿空间内的两个点 A、B。

下面我们看看笛卡儿空间中的三个点映射到霍夫空间的情况。在图 16-4 中，左图是笛卡儿空间，其中存在(0, 1)、(1, 2)、(2, 3)三个点。

下面从不同的角度分析笛卡儿空间中这三个点映射到霍夫空间的情况。

• 角度 1：笛卡儿空间内的一个点会映射为霍夫空间的一条线。
  例如，笛卡儿空间中的(0, 1)、(1, 2)、(2, 3)三个点映射到霍夫空间时，每个点对应着一条直线，对应关系如表 16-1 所示。

根据对应关系可知：

• 笛卡儿空间内的点(0, 1)，对应着霍夫空间内的直线 b = 1。
• 笛卡儿空间内的点(1, 2)，对应着霍夫空间内的直线 b = -k+2。
• 笛卡儿空间内的点(2, 3)，对应着霍夫空间内的直线 b = -2k+3。

从上述分析可知，笛卡儿空间内的三个点映射为霍夫空间内的三条直线。

• 角度 2：笛卡儿空间内的一条线会映射为霍夫空间的一个点。
  例如，笛卡儿空间中的(0, 1)、(1, 2)、(2, 3)三个点对应着直线 y = x+1，斜率 k 为 1，截距 b为 1。该直线 y = x+1 映射到霍夫空间内的点(1, 1)。
  从上述角度 1 和角度 2 的分析可知：
• 笛卡儿空间中的(0, 1)、(1, 2)、(2, 3)三个点会映射为霍夫空间内相交于点(1, 1)的三条直线。
• 笛卡儿空间中的(0, 1)、(1, 2)、(2, 3)三个点所连成（确定）的直线映射为霍夫空间内的点(1, 1)。

这说明，如果在笛卡儿空间内有三个点，并且它们能够连成一条 = 1 + 1的直线，那么在霍夫空间中，对应的点(k1, b1)上会有三条直线，分别对应着笛卡儿空间内的三个点。

到此，我们已经发现，如果在笛卡儿空间内，有 N 个点能够连成一条直线 = 1 + 1，那么在霍夫空间内就会有 N 条直线穿过对应的点(k1, b1) 。或者反过来说，如果在霍夫空间中，有越多的直线穿过点(k1, b1) ，就说明在笛卡儿空间内有越多的点位于斜率为 k1，截距为 b1的直线 = 1 + 1上。

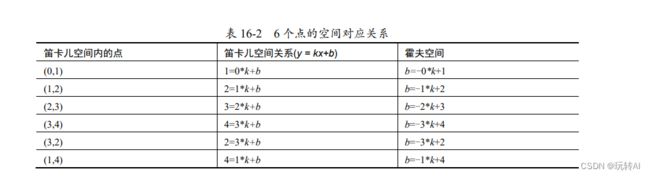
现在，我们看一个在笛卡儿空间内更多个点映射到霍夫空间的例子，也验证一下上述观点。在图 16-5 中，左图所示的是笛卡儿空间，其中有 6 个点，下面从不同的角度看下这 6 个点在右图霍夫空间的映射情况。

• 角度 1：笛卡儿空间的一点会映射为霍夫空间的一条线。
  笛卡儿空间中的 6 个点：(0, 1)、(1, 2)、(2, 3)、(3, 4)、(3, 2)、(1, 4)，映射到霍夫空间时，
  每个点对应着一条直线，对应关系如表 16-2 所示。

根据对应关系可知：

• 笛卡儿空间内的点(0, 1)，对应着霍夫空间内的直线 b = 1。
• 笛卡儿空间内的点(1, 2)，对应着霍夫空间内的直线 b = -k+2。
• 笛卡儿空间内的点(2, 3)，对应着霍夫空间内的直线 b = -2*k+3。
• 笛卡儿空间内的点(3, 4)，对应着霍夫空间内的直线 b = -3*k+4。
• 笛卡儿空间内的点(3, 2)，对应着霍夫空间内的直线 b = -3*k+2。
• 笛卡儿空间内的点(1, 4)，对应着霍夫空间内的直线 b = -1*k+4。

从上述分析可知，笛卡儿空间内的 6 个点映射为霍夫空间内的 6 条直线。

• 角度 2：笛卡儿空间的一条线会映射为霍夫空间的一个点。
  这里为了观察方便，将笛卡儿空间内连接了较多点的线绘制出来：连接点(0, 1)、(1, 2)、(2,3)、(3, 4)的线 LineA，连接点(2, 3)、(3, 2)、(1, 4)的线 LineB，连接点(0,1)、(3,2)的线 LineC，
  如图 16-6 的左图所示。

需要注意，在笛卡儿空间内，各个点之间存在多条直线。例如在点(1, 2)、(3, 2)之间，点(3,2)、(3, 4)之间，点(1, 4)、(3, 4)之间都存在着直线，这里做了简化，没有将上述直线都绘制出来。

下面分析笛卡儿空间内的三条直线 LineA、LineB、LineC 在霍夫空间内的映射情况。

• 直线 LineA 经过了 4 个点，表达式为 y = 1*x+1，斜率 k 为 1，截距 b 为 1，在霍夫空间内对应于点 A(1, 1)。

• 直线 LineB 经过了 3 个点，表达式为 y = -1*x+5，斜率 k 为-1，截距 b 为 5，在霍夫空间内对应于点 B(-1, 5)。

• 直线 LineC 经过了 2 个点，表达式为 y = -1/3*x+1，斜率 k 为-1/3，截距 b 为 1，在霍夫空间内对应于点 C(-1/3, 1)。

在图 16-6 中可以看到，右图所示的霍夫空间内点 A 有 4 条直线穿过，点 B 有 3 条直线穿过，点 C 有 2 条直线穿过。

分析上述关系：

• 霍夫空间内有 4 条直线穿过点 A。点 A 确定了笛卡儿空间内的一条直线，同时该直线穿过 4 个点，即霍夫空间内的点 A 确定了笛卡儿空间内的 LineA，该直线上包含(0, 1)、(1, 2)、(2, 3)、(3, 4)共 4 个点。

• 霍夫空间内有 3 条直线穿过点 B。点 B 确定了笛卡儿空间内的一条直线，同时该直线穿过 3 个点，即霍夫空间内的点 B 确定了笛卡儿空间内的 LineB，该直线上包含(2, 3)、(3,2)、(1, 4)共 3 个点。

• 霍夫空间内有 2 条直线穿过点 C。点 C 确定了笛卡儿空间内的一条直线，同时该直线穿过 2 个点，即霍夫空间内的点 C 确定了笛卡儿空间内的 LineC，该直线上包含(0, 1)、(2,3)共 2 个点。

综上所述，在霍夫空间内，经过一个点的直线越多，说明其在笛卡儿空间内映射的直线，是由越多的点所构成（穿过）的。我们知道，两个点就能构成一条直线。但是，如果有一个点是因为计算错误而产生的，那么它和另外一个点，也会构成一条直线，此时就会凭空构造出一条实际上并不存在的直线。这种情况是要极力避免的。因此，在计算中，我们希望用更多的点构造一条直线，以提高直线的可靠性。也就是说，如果一条直线是由越多点所构成的，那么它实际存在的可能性就越大，它的可靠性也就越高。因此，霍夫变换选择直线的基本思路是：选择有尽可能多直线交汇的点。

上面都是以我们熟悉的笛卡儿空间为例说明的。在笛卡儿空间中，可能存在诸如 x = x0的垂线 LineA 的形式，如图 16-7 所示。

此时，斜率 k 为无穷大，截距 b 无法取值。因此，图 16-7 中的垂线 LineA 无法映射到霍夫空间内。为了解决上述问题，可以考虑将笛卡儿坐标系映射到极坐标系上，如图 16-8 所示

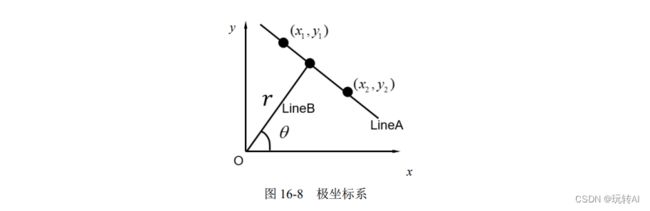
在笛卡儿坐标系内使用的是斜率 k 和截距 b，即用(k, b)表示一条直线。在极坐标系内，采用极径 r（有时也用表示）和极角来表示，即(r, θ)来表示。极坐标系中的直线可以表示为：

= cos + sin

例如，图 16-8 中的直线 LineA，可以使用极坐标的极径 r 和极角来表示。其中，r 是直线LineA 与图像原点 O 之间的距离，参数是直线 LineA 的垂线 LineB 与 x 轴的角度。在这种表示方法中，图像中的直线有一个（0~π）的角，而 r 的最大值是图像对角线的长度。

用这种表示方法，可以很方便地表示图 16-7 中的 3 个点所构成的直线。与笛卡儿空间和霍夫空间的映射关系类似：

• 极坐标系内的一个点映射为霍夫坐标系（霍夫空间）内的一条线（曲线）。
• 极坐标系内的一条线映射为霍夫坐标系内的一个点。

一般来说，在极坐标系内的一条直线能够通过在霍夫坐标系内相交于一点的线的数量来评估。在霍夫坐标系内，经过一个点的线越多，说明其映射在极坐标系内的直线，是由越多的点所构成（穿过）的。

因此，霍夫变换选择直线的基本思路是：选择由尽可能多条线汇成的点。通常情况下，设置一个阈值，当霍夫坐标系内交于某点的曲线达到了阈值，就认为在对应的极坐标系内存在（检测到）一条直线。

上述内容是霍夫变换的原理，即使完全不理解上述原理，也不影响我们使用 OpenCV 提供的霍夫变换函数来进行霍夫变换。OpenCV 本身是一个黑盒子，它给我们提供了接口（参数、返回值），我们只需要掌握接口的正确使用方法，就可以正确地处理图像问题，无须掌握其内部工作原理。

在某种情况下，OpenCV 库和 Photoshop 等图像处理软件是类似的，只要掌握了它们的使用方法，就能够得到正确的处理结果。在进行图像处理时，并不需要我们关注其实现原理等技术细节。但是，如果我们进一步了解其工作原理，对我们的工作也是有大有裨益的。

HoughLines函数

OpenCV 提供了函数 cv2.HoughLines()用来实现霍夫直线变换，该函数要求所操作的源图
像是一个二值图像，所以在进行霍夫变换之前要先将源图像进行二值化，或者进行 Canny 边缘检测。
函数 cv2.HoughLines()的语法格式为：

lines=cv2.HoughLines(image, rho, theta, threshold)

式中：

• image 是输入图像，即源图像，必须是 8 位的单通道二值图像。如果是其他类型的图像，
  在进行霍夫变换之前，需要将其修改为指定格式。
• rho 为以像素为单位的距离 r 的精度。一般情况下，使用的精度是 1。
• theta 为角度的精度。一般情况下，使用的精度是π/180，表示要搜索所有可能的角度。
• threshold 是阈值。该值越小，判定出的直线就越多。通过上一节的分析可知，识别直线
  时，要判定有多少个点位于该直线上。在判定直线是否存在时，对直线所穿过的点的数量进行评估，如果直线所穿过的点的数量小于阈值，则认为这些点恰好（偶然）在算法上构成直线，但是在源图像中该直线并不存在；如果大于阈值，则认为直线存在。所以，如果阈值较小，就会得到较多的直线；阈值较大，就会得到较少的直线。
• 返回值 lines 中的每个元素都是一对浮点数，表示检测到的直线的参数，即(r, θ)，是numpy.ndarray 类型。

有一点需要强调的是，使用函数 cv2.HoughLines()检测到的是图像中的直线而不是线段，因此检测到的直线是没有端点的。所以，我们在进行霍夫直线变换时所绘制的直线都是穿过整幅图像的。

绘制直线的方法是，对于垂直方向的直线（不是指垂线，是指垂直方向上的各种角度的直线），计算它与图像水平边界（即图像中的第一行和最后一行）的交叉点，然后在这两个交叉点之间画线。对于水平方向上的直线，采用类似的方式完成，只不过用到的是图像的第一列和最后一列。在绘制线时，所使用的函数是 cv2.line()。该函数方便的地方在于，即使点的坐标超出了图像的范围，它也能正确地画出线来，因此没有必要检查交叉点是否位于图像内部。
遍历函数 cv2.HoughLines()的返回值 lines，就可以绘制出所有的直线。

示例：使用函数 cv2.HoughLines()对一幅图像进行霍夫变换，并观察霍夫变换的效果。

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('computer.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)
orgb=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
oShow=orgb.copy()
lines = cv2.HoughLines(edges,1,np.pi/180,140)
for line in lines:
 rho,theta = line[0]
 a = np.cos(theta)
 b = np.sin(theta)
 x0 = a * rho
 y0 = b * rho
 x1 = int(x0 + 1000 * (-b))
 y1 = int(y0 + 1000 * (a))
 x2 = int(x0 - 1000 * (-b))
 y2 = int(y0 - 1000 * (a))
 cv2.line(orgb, (x1, y1), (x2, y2), (0, 0, 255), 2)
plt.subplot(121)
plt.imshow(oShow)
plt.axis('off')
plt.subplot(122)
plt.imshow(orgb)
plt.axis('off')
plt.show()

运行结果：

右图中，较粗的直线是因为有多条直线靠近在一起，即检测出了重复的结果。在一些情况下，使用霍夫变换可能将图像中有限个点碰巧对齐的非直线关系检测为直线，而导致误检测，尤其是一些复杂背景的图像，误检测会很明显。此图中该问题虽然并不是特别明显，但是如果将阈值 threshold 的值设置得稍小些，仍然会出现较多重复的检测结果

OpenCV 官网提供了一幅名为 building.jpg 的图像用来测试，大家可以下载该图像，对其进行霍夫变换，观察检测的效果。该图在使用霍夫变换进行检测时，存在非常严重的误检测。为了解决上述问题，人们提出了霍夫变换的改进版——概率霍夫变换。

HoughLinesP函数

概率霍夫变换对基本霍夫变换算法进行了一些修正，是霍夫变换算法的优化。它没有考虑所有的点。相反，它只需要一个足以进行线检测的随机点子集即可。为了更好地判断直线（线段），概率霍夫变换算法还对选取直线的方法作了两点改进：

• 所接受直线的最小长度。如果有超过阈值个数的像素点构成了一条直线，但是这条直线很短，那么就不会接受该直线作为判断结果，而认为这条直线仅仅是图像中的若干个像素点恰好随机构成了一种算法上的直线关系而已，实际上原图中并不存在这条直线。

• 接受直线时允许的最大像素点间距。如果有超过阈值个数的像素点构成了一条直线，但是这组像素点之间的距离都很远，就不会接受该直线作为判断结果，而认为这条直线仅仅是图像中的若干个像素点恰好随机构成了一种算法上的直线关系而已，实际上原始图像中并不存在这条直线。

在 OpenCV 中，函数 cv2.HoughLinesP()实现了概率霍夫变换。其语法格式为：

lines =cv2.HoughLinesP(image, rho, theta, threshold, minLineLength,
maxLineGap)

式中参数与返回值的含义如下：

• image 是输入图像，即源图像，必须为 8 位的单通道二值图像。对于其他类型的图像，在进行霍夫变换之前，需要将其修改为这个指定的格式。
• rho 为以像素为单位的距离 r 的精度。一般情况下，使用的精度是 1。
• theta 是角度的精度。一般情况下，使用的精度是 np.pi/180，表示要搜索可能的角度。
• threshold 是阈值。该值越小，判定出的直线越多；值越大，判定出的直线就越少。
• minLineLength 用来控制“接受直线的最小长度”的值，默认值为 0。
• maxLineGap 用来控制接受共线线段之间的最小间隔，即在一条线中两点的最大间隔。如果两点间的间隔超过了参数 maxLineGap 的值，就认为这两点不在一条线上。默认值为 0。
• 返回值 lines 是由 numpy.ndarray 类型的元素构成的，其中每个元素都是一对浮点数，表
  示检测到的直线的参数，即(r, θ)。

代码示例：使用函数 cv2.HoughLinesP()对一幅图像进行霍夫变换，并观察图像的检测效果。

示例原图

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('computer.jpg',-1)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize =3)
orgb=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
oShow=orgb.copy()
lines = cv2.HoughLinesP(edges,1,np.pi/180,1,minLineLength=100,maxLineGap=10)
for line in lines:
 x1,y1,x2,y2 = line[0]
 cv2.line(orgb,(x1,y1),(x2,y2),(255,0,0),5)
plt.subplot(121)
plt.imshow(oShow)
plt.axis('off')
plt.subplot(122)
plt.imshow(orgb)
plt.axis('off')
plt.show()

运行结果：

可以看到概率霍夫变换比霍夫变换得到的检测结果更准确。

霍夫圆环变换

霍夫变换除了用来检测直线外，也能用来检测其他几何对象。实际上，只要是能够用一个参数方程表示的对象，都适合用霍夫变换来检测。

用霍夫圆变换来检测图像中的圆，与使用霍夫直线变换检测直线的原理类似。在霍夫圆变换中，需要考虑圆半径和圆心（x 坐标、y 坐标）共 3 个参数。

在 OpenCV 中，采用的策略是两轮筛选。第 1 轮筛选找出可能存在圆的位置（圆心）；第 2 轮再根据第 1 轮的结果筛选出半径大小。与用来决定是否接受直线的两个参数“接受直线的最小长度（minLineLength）”和“接受直线时允许的最大像素点间距（MaxLineGap）”类似，霍夫圆变换也有几个用于决定是否接受圆的参数：圆心间的最小距离、圆的最小半径、圆的最大半径。

在 OpenCV 中，实现霍夫圆变换的是函数 cv2.HoughCircles()，该函数将 Canny 边缘检测和霍夫变换结合。其语法格式为：

circles=cv2.HoughCircles(image, method, dp, minDist, param1, param2,
minRadius, maxRadius)

式中参数与返回值的含义如下：

• image：输入图像，即源图像，类型为 8 位的单通道灰度图像。
• method：检测方法。截止到 OpenCV 4.0.0-pre 版本，HOUGH_GRADIENT 是唯一可用的参数值。该参数代表的是霍夫圆检测中两轮检测所使用的方法。
• dp：累计器分辨率，它是一个分割比率，用来指定图像分辨率与圆心累加器分辨率的比
  例。例如，如果 dp=1，则输入图像和累加器具有相同的分辨率。
• minDist：圆心间的最小间距。该值被作为阈值使用，如果存在圆心间距离小于该值的多个圆，则仅有一个会被检测出来。因此，如果该值太小，则会有多个临近的圆被检测出来；如果该值太大，则可能会在检测时漏掉一些圆。
• param1：该参数是缺省的，在缺省时默认值为 100。它对应的是 Canny 边缘检测器的高阈值（低阈值是高阈值的二分之一）。
• param2：圆心位置必须收到的投票数。只有在第 1 轮筛选过程中，投票数超过该值的圆，才有资格进入第 2 轮的筛选。因此，该值越大，检测到的圆越少；该值越小，检测到的圆越多。这个参数是缺省的，在缺省时具有默认值 100。
• minRadius：圆半径的最小值，小于该值的圆不会被检测出来。该参数是缺省的，在缺省时具有默认值 0，此时该参数不起作用。
• maxRadius：圆半径的最大值，大于该值的圆不会被检测出来。该参数是缺省的，在缺省时具有默认值 0，此时该参数不起作用。
• circles：返回值，由圆心坐标和半径构成的 numpy.ndarray。

需要特别注意，在调用函数 cv2.HoughLinesCircles()之前，要对源图像进行平滑操作，以减少图像中的噪声，避免发生误判。

该函数具有非常多的参数，在实际检测中可以根据需要设置不同的值。

示例：使用 HoughLinesCircles 函数对一幅图像进行霍夫圆变换，并观察检测效果。

原图：

代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('chess.jpg',0)
imgo=cv2.imread('chess.jpg',-1)
o=cv2.cvtColor(imgo,cv2.COLOR_BGR2RGB)
oshow=o.copy()
img = cv2.medianBlur(img,5)
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,300,
param1=50,param2=30,minRadius=100,maxRadius=200)
circles = np.uint16(np.around(circles))
for i in circles[0,:]:
 cv2.circle(o,(i[0],i[1]),i[2],(255,0,0),12)
 cv2.circle(o,(i[0],i[1]),2,(255,0,0),12)
plt.subplot(121)
plt.imshow(oshow)
plt.axis('off')
plt.subplot(122)
plt.imshow(o)
plt.axis('off')
plt.show()

运行结果：

可以看到霍夫圆变换检测到了源图像中的三个圆。
为了方便读者在纸质版图书上观察，本例中圆环和圆心都是用红色显示的，在实际使用中可以设置函数 cv2.circle()中的颜色参数，显示不同的颜色。

---

1. “笛卡儿” 可能是指法国哲学家、数学家、科学家笛卡尔（René Descartes），他在数学、哲学和科学领域都有重要贡献。其中，他的坐标几何学思想为现代数学和计算机图形学的发展做出了重要贡献。
   笛卡尔几何学，也称为解析几何学，是通过代数方程和坐标系统来研究几何问题的一种方法。笛卡尔引入了笛卡尔坐标系，将几何问题转化为代数方程，从而使几何问题得以用代数方法求解。这种方法为几何学与代数学之间的紧密关联奠定了基础，并对现代数学和计算机图形学的发展产生了深远影响。 ↩︎