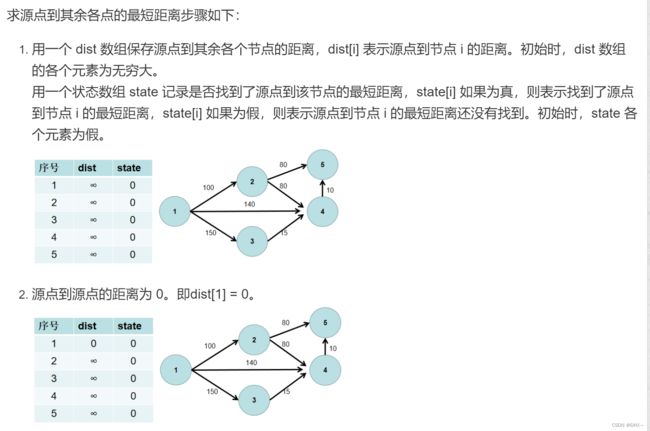
单源最短路
最重要的是问题的转化和抽象 把问题转化成最短路的模板
无负环
Dijkstra 迪杰斯特拉算法 采用的贪心的策略
每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止
Dijkstra求最短路 I
朴素版 O(n^2)
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500
1≤m≤10^5(稠密图)
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3#include
#include
#include
using namespace std;
const int N=550;
int g[N][N];//存储各个边之间的距离
int dist[N];//1到各个点之间的距离
bool st[N];//标记数组
int n,m;
int dijkstra()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=1;i<=n;i++)
{
int t=-1;//将t设置为-1 因为Dijkstra算法适用于不存在负权边的图
//每次都找到距离没有被标记并且距离原点最近的点
for(int j=1;j<=n;j++)
{
if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;
}
st[t]=1;//找到距离原点还没有被标记的最近的点 标记
//找到最近的点 然后取更新
for(int j=1;j<=n;j++)
{
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
}
return dist[n];
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;cin>>a>>b>>c;
g[a][b]=min(g[a][b],c);
}
int num=dijkstra();
if(num==0x3f3f3f3f) cout<<"-1"< Dijkstra求最短路 II(堆优化版)
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z 表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×10^5(稀疏图)
图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 10^9。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3时间复杂度 O(mlogn)
每次找到最小距离的点沿着边更新其他的点,若dist[j] > distance + w[i],表示可以更新dist[j],更新后再把j点和对应的距离放入小根堆中。由于点的个数是n,边的个数是m,在极限情况下(稠密图m=n(n−1)/2)最多可以更新m回,每一回最多可以更新n个点(严格上是n - 1个点),有m回,因此最多可以把n^2个点放入到小根堆中,因此每一次更新小根堆排序的情况是O(log(n^2)),一共最多m次更新,因此总的时间复杂度上限是O(mlog((n^2)))=O(2mlogn)=O(mlogn)
利用小根堆 直接找出距离原点最近的点O(logn) 然后取更新与它相关的点即可
#include
#include
#include
#include
using namespace std;
typedef pairPII;
const int N=1e6+10;
int dist[N];
int h[N],ne[N],e[N],w[N],idx;
bool st[N];
int n,m;
void add(int a,int b,int c)
{
e[idx]=b;//存储结点
w[idx]=c;//边权
ne[idx]=h[a];//改变指向
h[a]=idx;
idx++;
}
int dijkstra()
{
memset(dist,0x3f,sizeof dist);//初始化
dist[1]=0;//原点到原点之间的距离是0
priority_queue,greater >heap;//小根堆
heap.push({0,1});//先存储距离 在存储节点 pair是按照第一个去排大小的然后再是第二个
while(heap.size())
{
//选取距离原点最小的点
auto t=heap.top();
heap.pop();
int ver=t.second,distance=t.first;
if(st[ver]) continue;//若是标记过就不进行下面的更新了
st[ver]=true;
for(int i=h[ver];i!=-1;i=ne[i])
{
/*在建表的过程中 e[idx]=b,w[idx]=c,ne[idx]=h[a],
h[a]=idx(此时已经改变了h[a]的值,h[a]的值不在是-1 h[a]代表了新的idx指向了b 此时b的ne[]指向了-1)
h[a]=idx 便是b的idx 故e[i]是点 w[i]是 a到b的权重
idx++
*/
//更改与之相邻的边
int j=e[i];
if(dist[j]>dist[ver]+w[i])
{
dist[j]=dist[ver]+w[i];
heap.push({dist[j],j});
}
}
}
return dist[n];
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--)
{
int a,b,c;cin>>a>>b>>c;
add(a,b,c);
}
int t=dijkstra();
if(t==0x3f3f3f3f) cout<<"-1"< 有负环 spfa 算法
spfa求最短路
时间复杂度 O(m)
时间复杂度 一般:O(m)O(m) 最坏:O(nm)
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible。
数据保证不存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围
1≤n,m≤10^5,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3
1 2 5
2 3 -3
1 3 4
输出样例:
2在Bellman中, 不论这个点是否能够从1出发到达, 在循环的过程中都会更新它的dist
在spfa中, 只会更新与连通的相邻的边, 对于那些不可达点,并不会影响它的dist
dist[5] = 0x3f3f3f3f, dist[6] = 0x3f3f3f3f, 5和6之间有一条负权边 -100, 在图中都不可能从 1 出发到达 5 和 6
在Bellman中, 会把dist[6] = 0x3f3f3f3f - 100
在spfa中, 不会对dist[6]做任何改动,因为 5 连不到 1, 不会被放进队列里
//最后在判断上,Bellman中不可达的点有很多种取值情况, 而spfa中只有一种情况, 所以采取不同的方式
#include
#include
#include
#include
using namespace std;
const int N=101000;
int h[N],w[N],ne[N],e[N],idx;
int dist[N];
bool st[N];
int n,m;
//建图
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int spfa()
{
//初始化
memset(dist,0x3f,sizeof dist);
//原点到原点的距离为0
dist[1]=0;
queueq;
//将原点(起始点)入队列
q.push(1);
//表示这个点在队列中
st[1]=true;
while(q.size())//不断进行松弛
{
int t=q.front();
q.pop();
//表示该点已经被弹出 不在队列中 一个点可能反反复复进入队列中不断的去更新
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])//遍历所有和t相连的点
{
int j=e[i];
//判断是否该点距离原点是否变短
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
//判断变短的该点是否已经在队列中了
if(!st[j])
{
//没有则入队
q.push(j);
st[j]=true;
}
}
}
}
return dist[n];
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);//初始化邻接表
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);//加入到邻接表
}
int t=spfa();
if(t==0x3f3f3f3f) puts("impossible");//如果到n点的距离是无穷,则不能到达
else printf("%d\n",t);//否则能到达,输出距离
return 0;
} spfa判断负环
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你判断图中是否存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z 表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
如果图中存在负权回路,则输出 Yes,否则输出 No。
数据范围
1≤n≤2000
1≤m≤10000
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3
1 2 -1
2 3 4
3 1 -4
输出样例:
Yes
负权边不是关键,关键是负环。dist 可以初始化,也可以不初始化,dist 初始值的大小不影响最终结果。
不管dist数组的初值是多少,都是可以的。因为只要有负环存在,就必然有某些点的距离是负无穷,所以不管距离被初始化成何值,都一定严格大于负无穷,所以一定会被无限更新。
这里是判断此图中是否存在负环,所以要将所有的点都加入队列中,那每一个节点的dist值不都设为0就好了吗?况且负环的话即使dist数组的每一个值都为0,也会被一直更新。
#include
#include
#include
#include
using namespace std;
const int N=100100;
int h[N],w[N],e[N],ne[N],idx;
int dist[N],cnt[N];//cnt[x]表示x点到虚拟原点的边数
int n,m;
bool st[N];
//创立图
void add(int a,int b,int c)
{
e[idx]=b;w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
bool spfa()
{
queueq;
//将所有的点都推入队列中
for(int i=1;i<=n;i++)
{
st[i]=true;
q.push(i);
}
while(q.size())
{
//逐一弹出队列 更新
int t=q.front();
q.pop();st[t]=false;
//更新与之相邻的边是否变小
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
//代表该点到需要原点有n 条边 这不可能 故存在负环
if(cnt[j]>=n) return true;
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
if(spfa()) puts("Yes");
else puts("No");
return 0;
} 信使
战争时期,前线有 n 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。
信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。
指挥部设在第一个哨所。
当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。
当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。信在一个哨所内停留的时间可以忽略不计。
直至所有 n 个哨所全部接到命令后,送信才算成功。
因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他 k 个哨所有通信联系的话,这个哨所内至少会配备 k 个信使)。
现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。
输入格式
第 1 行有两个整数 n 和 m,中间用 1 个空格隔开,分别表示有 n 个哨所和 m 条通信线路。
第 22 至 m+1 行:每行三个整数 i、j、k中间用 1 个空格隔开,表示第 i 个和第 j 个哨所之间存在 双向 通信线路,且这条线路要花费 k 天。
输出格式
一个整数,表示完成整个送信过程的最短时间。
如果不是所有的哨所都能收到信,就输出-1。
数据范围
1≤n≤100
1≤m≤200
1≤k≤1000
输入样例:
4 4
1 2 4
2 3 7
2 4 1
3 4 6
输出样例:
11核心:对于每个点来说,它接收到信的时间,等于它到指挥部的最短距离
遍历一下每个点到指挥部的最短距离,取最大值即可
若最大值为0x3f3f3f3f说明不通 故-1
#include
#include
#include
#include
using namespace std;
const int N=110;
int g[N][N];
int n,m;
int dist[N];
bool st[N];
void dijkstra()
{
memset(dist,0x3f,sizeof dist);
queueq;
q.push(1);
dist[1]=0;
for(int i=1;i<=n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
{
if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;
}
st[t]=true;
for(int j=1;j<=n;j++)
{
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
}
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);
}
dijkstra();
int num=0;
int max1=0;
for(int i=1;i<=n;i++)
{
max1=max(max1,dist[i]);
}
if(max1==0x3f3f3f3f) cout<<"-1"< 香甜的黄油
(多源汇最短路 但是它会超时 然后用堆优化版Dijkstra() 或者 spfa()取写)
农夫John发现了做出全威斯康辛州最甜的黄油的方法:糖。
把糖放在一片牧场上,他知道 N 只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。
当然,他将付出额外的费用在奶牛上。
农夫John很狡猾,就像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。
他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。
农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。
给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。
数据保证至少存在一个牧场和所有牛所在的牧场连通。
输入格式
第一行: 三个数:奶牛数 N,牧场数 P,牧场间道路数 C。
第二行到第 N+1 行: 1 到 N 头奶牛所在的牧场号。
第 N+2 行到第 N+C+1 行:每行有三个数:相连的牧场A、B,两牧场间距 D,当然,连接是双向的。
输出格式
共一行,输出奶牛必须行走的最小的距离和。
数据范围
1≤N≤500
2≤P≤800
1≤C≤1450
1≤D≤255
输入样例:
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5
输出样例:
8是一道最短路的升级应用,根据题意, 我们需要找到一个距离所有牛最短的牧场。那么只需要枚举所有牧场为起点,求此时所有其他牧场到它的最短路之和即可。然后输出所有牧场中最短距离即为答案。
spfa
#include
#include
#include
#include
using namespace std;
const int N=810,M=3100;
int h[N],ne[M],e[M],w[M],idx;
int dist[N];
int id[N];
bool st[N];
int n,p,c;
void add(int a,int b,int c1)
{
e[idx]=b;
w[idx]=c1;
ne[idx]=h[a];
h[a]=idx++;
}
int spfa(int x)
{
memset(dist,0x3f,sizeof dist);
memset(st,0,sizeof st);
queueq;
q.push(x);
dist[x]=0;
st[x]=1;
while(q.size())
{
auto t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
if(!st[j])
{
q.push(j);
st[j]=1;
}
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
int y=id[i];
if(dist[y]==0x3f3f3f3f) return 0x3f3f3f3f;
ans+=dist[y];
}
return ans;
}
int main()
{
cin>>n>>p>>c;
for(int i=1;i<=n;i++) cin>>id[i];
memset(h,-1,sizeof h);
while(c--)
{
int a,b,c1;cin>>a>>b>>c1;
add(a,b,c1);
add(b,a,c1);
}
int ans=0x3f3f3f3f;
//遍历每个点当起点 取最小值
for(int i=1;i<=p;i++)
{
ans=min(ans,spfa(i));
}
cout< Dijkstra 堆优化版
#include
#include
#include
#include
using namespace std;
const int N=810,M=3000,INF=0x3f3f3f3f;
typedef pairPII;
int h[N],ne[M],e[M],w[M],idx;
int dist[N];
bool st[N];
int id[N];
int n,p,c;
void add(int a,int b,int x)
{
e[idx]=b;
w[idx]=x;
ne[idx]=h[a];
h[a]=idx++;
}
int dijkstra(int x)
{
memset(dist,0x3f,sizeof dist);
memset(st,0,sizeof st);
dist[x]=0;
priority_queue,greater>heap;
heap.push({0,x});
while(heap.size())
{
auto t=heap.top();
heap.pop();
int ver=t.second;
if(st[ver]) continue;
st[ver]=true;
for(int i=h[ver];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[ver]+w[i])
{
dist[j]=dist[ver]+w[i];
if(!st[j])
{
heap.push({dist[j],j});
}
}
}
}
int res=0;
for(int i=1;i<=n;i++)
{
int y=id[i];
if(dist[y]==INF) return INF;
res+=dist[y];
}
return res;
}
int main()
{
cin>>n>>p>>c;
for(int i=1;i<=n;i++) cin>>id[i];
memset(h,-1,sizeof h);
while(c--)
{
int a,b,x;cin>>a>>b>>x;
add(a,b,x);
add(b,a,x);
}
int ans=INF;
for(int i=1;i<=p;i++)
{
ans=min(ans,dijkstra(i));
}
cout< 最小花费
在 n 个人中,某些人的银行账号之间可以互相转账。
这些人之间转账的手续费各不相同。
给定这些人之间转账时需要从转账金额里扣除百分之几的手续费,请问 A 最少需要多少钱使得转账后 B 收到 100 元。
输入格式
第一行输入两个正整数 n,m 分别表示总人数和可以互相转账的人的对数。
以下 m 行每行输入三个正整数 x,y,z,表示标号为 x 的人和标号为 y 的人之间互相转账需要扣除 z% 的手续费 ( z<100)。
最后一行输入两个正整数 A,B。
数据保证 A 与 B 之间可以直接或间接地转账。
输出格式
输出 A 使得 B 到账 100 元最少需要的总费用。
精确到小数点后 8 位。
数据范围
1≤n≤2000
m≤10^5
输入样例:
3 3
1 2 1
2 3 2
1 3 3
1 3
输出样例:
103.07153164100=T*w1*w2*w3*w4*w5*w6*...wn
T=100/(w1*w2*w3*w4*....*wn)
若想是T最小 则求w1*w2*...wn最大 就是S到T之间的边的权重乘积最大
#include
#include
#include
using namespace std;
const int N=2100;
double g[N][N];
double dist[N];
bool st[N];
int n,m,s,t;
void dijkstra()
{
dist[s]=1;
for(int i=1;i<=n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
{
if(!st[j]&&(t==-1||dist[j]>dist[t])) t=j;
}
st[t]=true;
for(int j=1;j<=n;j++)
{
dist[j]=max(dist[j],dist[t]*g[t][j]);
}
}
}
int main()
{
scanf("%d%d",&n,&m);
while(m--)
{
int a,b,c;scanf("%d%d%d",&a,&b,&c);
double z=(100.0-c)/100;
g[a][b]=g[b][a]=max(g[a][b],z);
}
scanf("%d%d",&s,&t);
dijkstra();
printf("%.8lf\n",100/dist[t]);
return 0;
}