算法之枚举及其优化(1)——百钱百鸡问题的多种解法(一重循环解决)
目录
写在前面:
从百钱百鸡问题说起
直接枚举(暴力破解)
开始优化(缩小枚举范围)
继续优化(二重循环)
最终优化(一重循环)
总结
写在后面
写在前面:
本文适合初学者学习,鉴于本人能力有限以及希望读者可以在最短的时间内获得最高的收益的原则,本人不阐述过多的专业术语以及底层知识,简明扼要,精简文字,避免文章晦涩冗长。
考虑到学习枚举的同学可能没有学过C++,本文代码完全使用C来实现。有的初学者可能是为了学习“百钱百鸡问题”而来,所以笔者不讲述时间复杂度的概念,而是以clock()函数直接显示程序计算时间,虽然略有不妥,却也能在一定程度上反映算法的优劣。(您大可不必在意这个clock函数,它只是一个显示时间的函数而已)
从百钱百鸡问题说起
关于枚举,我们从一个经典的百钱百鸡问题说起:
题目:我国古代数学家张丘建在《算经》一书中曾提出过著名的“百钱买百鸡”问题,该问题叙述如下:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何? 翻译过来,意思是公鸡一个五块钱,母鸡一个三块钱,小鸡三个一块钱,现在要用一百块钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?
直接枚举(暴力破解)
对于此题,我们有一种无脑思路,就是将每一种买鸡的情况罗列出来,由计算机来检查是否符合题目的要求,我们很容易通过程序来解决这个问题,如下:
# include
int main()
{
int x,y,z;//x为公鸡,y为母鸡,z为小鸡
for(x=0;x<100;x++)
for(y=0;y<100;y++)
for(z=0;z<100;z+=3){
if(x+y+z==100&&5*x+3*y+z/3==100){
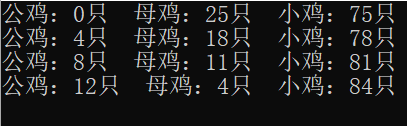
printf("公鸡:%d只 母鸡:%d只 小鸡:%d只\n",x,y,z);
}
}
return 0;
} 输出结果:
很简单,我们便得到了答案。这时可能就有同学要说了:“就这?这么简单,还用你来说吗?”但是,枚举之所以能称为算法,自然不会这么简单!如果你对枚举的认知只是到此为止的话,你可能就会写出下面这种代码:
我们来看看这个代码,八重循环+40多个联结的逻辑判断语句,时间复杂度已经爆表,这样的程序从实用性上来说,实用性几乎为0。即使是提交到OJ上也只是会得到“运行超时”的结果,可谓是百无一用。好在这份代码中所给的数据较小,只是个位数。但凡数据稍微大一点,运行时间。。。(emmm......自己体会叭)
开始优化(缩小枚举范围)
对于枚举,我们可以进行优化,而不是单单像上面那样无脑列出每一个结果,那么该如何优化呢?这就需要我们从题目中获取信息了。首先我们想,是否可以缩小枚举数据的范围,从而减少枚举的情况个数。对于本题,我们不难发现,公鸡和母鸡的数目不用从0枚举到100,买到的公鸡在达到20只时,就已经达到了预期的100元。同理,母鸡不能超过33只,据此,我们可以修改程序,将循环的范围缩小。同时,在程序中加入clock()函数,以此检查程序运行的速度是否变快。为了减小误差带来的影响,我们不妨将题目改为万钱万鸡问题(笔者以此刻意地增加运行时间,以此减小误差对实验结果的影响)。代码如下:
# include
# include
int main()
{
int x,y,z;//x为公鸡,y为母鸡,z为小鸡
for(x=0;x<2000;x++)
for(y=0;y<3333;y++)
for(z=0;z<10000;z+=3){
if(x+y+z==10000&&5*x+3*y+z/3==10000){
printf("公鸡:%d只 母鸡:%d只 小鸡:%d只\n",x,y,z);
}
}
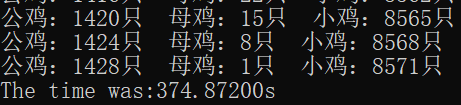
printf("The time was:%.5lfs",(double)clock()/CLOCKS_PER_SEC);
return 0;
} 运行结果
我们再来对比优化前的结果
OK,我们明显可以发现,优化前后两者运行时间的区别,看来枚举也不是完全无脑的!
继续优化(二重循环)
我们来进一步思考,仅仅是缩小了循环的终止条件,运行时间就差距如此之大,我们不妨想办法直接去掉一重循环,那么运行时间必然可以更快!
我们不妨这样想,我们先确定公鸡和母鸡的个数,然后剩下的钱全部用来买小鸡,我们只需要判断能不能正好花完10000元,以及是否正好买到10000只鸡即可,于是我们将判断条件改为
if((5*x+3*y+(10000-x-y)/3.0)==10000)如果5*x+3*y+(10000-x-y)/3.0的值不是整数,则表示不能正好花完10000元;在该式值为整数的情况下,我们判断其值是否为10000,为真则表示买到了10000只鸡,符合题目要求。完整代码如下:
# include
# include
int main()
{
int x,y;//x为公鸡,y为母鸡,z为小鸡
for(x=0;x<2000;x++)
for(y=0;y<3333;y++){
if((5*x+3*y+(10000-x-y)/3.0)==10000){
printf("公鸡:%d只 母鸡:%d只 小鸡:%d只\n",x,y,(10000-x-y)/3);
}
}
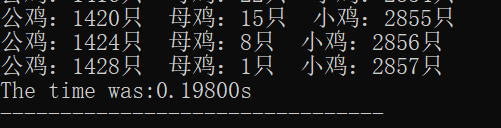
printf("The time was:%.5lfs",(double)clock()/CLOCKS_PER_SEC);
return 0;
} 运行结果:
我们惊讶地发现,运行时间居然直接缩小了两个量级!
最终优化(一重循环)
在尝到直接削去一重循环带来的甜头后,不知足的我们又开始想,是否可以再削去一重循环,只用一重循环来解决呢?我们反观上面的二重循环,发现我们并没有使用z这个变量了,那么我们在只使用一重循环的时候,是否也应该只使用一个变量呢?我们想到,x,y,z之间并不是毫无联系的,我们假设万钱刚好买到万鸡,据此我们列出两个方程组:
5*x+3*y+z/3=10000
x+y+z=10000
我们进行数学消元,只保留x,得到y=2500-7*x/4和z=7500+3*x/4,这是我们假设条件成立得到的关系式,下面我们只需令x取不同的值,同时对y和z进行检查,若x,y,z均满足我们预设的条件,那么这组解就是有效的。对于y,我们要令其为非负数,所以x不能大于1428;对于z,我们要令其为3的倍数。此外,我们得到的y和z两个关于x的关系式是由假设上述两个方程组成立得到的,所以我们的解还需要满足上述两个关系式。据此,我们得到以下的代码:
# include
int main()
{
int x,y,z;//x为公鸡,y为母鸡,z为小鸡
for(x=0;x<1429;x++){
y = 2500-7*x/4;
z = 7500+3*x/4;
if((x+y+z==10000)&&(5*x+3*y+z/3==10000)&&(z%3==0))
printf("公鸡:%d只 母鸡:%d只 小鸡:%d只\n",x,y,(10000-x-y)/3);
}
return 0;
} 这时由于其运行时间已经很小,我们再比较运行时间受误差的影响很大,不能再比较运行时间。但是我们可以通过比较循环次数来对比两种算法,在二重循环,我们的循环次数是2000*3333=6666000次,而在一重循环中,我们的循环次数仅仅是1429次,缩小了三个量级,那么运行速度理所应当地更快了。
总结
通过上面的不断优化,对于万钱万鸡的问题,我们成功地将循环次数从百万亿次减少到了1429次,所以,枚举并不一定是很简单很暴力的算法,一般的暴力枚举是不能通过OJ评测的,所以我们必须寻求优化,本文仅仅通过一个简单题来介绍优化的重要性,下一篇笔者将通过难度较高的“熄灯问题”为大家进一步介绍枚举算法及其优化。
写在后面
鉴于本人能力以及时间关系,如果有技术性错误,烦请各位不吝赐教,私信指出,谢谢!