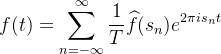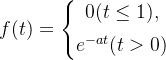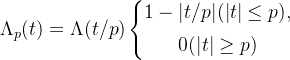Fourier变换及其应用(Brad G. Osgood)——第2章——Fourier变换
第2章 Fourier变换
2.1 初识Fourier变换(A First Look at the Fourier Transform)
我们即将从Fourier级数过渡到Fourier变换。“过渡(transition)”是合适的词,因为我们选择了Fourier变换从周期函数到非周期函数的引出路径。 为了完成这一旅程,我们将把非周期函数(几乎可以是任何非周期函数)视为周期变得越来越大的周期函数极限情况。事实上,这个过程并不会立即产生预期的结果。需要一些额外的修改才能从Fourier系数中导出Fourier变换,但我们会轻松着陆,这是一次有趣的旅行(excursion)。
2.1.1 一个例子:矩形函数及其Fourier变换(An example: The rectangle function and its Fourier transform)
让我们举一个具体的、简单的、并且十分重要的例子。考虑一个矩形函数,或者简称“矩形(rect)”,定义为
下面图1 是其图像,并不是很复杂。
---------------------------------------------图2.1. 矩形函数的图像-------------------------------------------------
Π(t)是偶函数——中心位于原点,宽度为1。稍后我们会考虑平移和缩放版本。你可以将Π(t)视为是对一个开关进行建模,它在1秒内处于打开状态,在1秒以外处于关闭状态。也有各种其它称谓,比如,“顶帽函数(top hat)”(缘于其图像的形状),指示函数(indicator function),或者区间(-1/2,1/2)的特征函数(characteristic function)。
关于端点的定义,常见的约定是定义Π(±1/2) = 1 或Π(±1/2) = 1/2,而我们将其定义为Π(±1/2) = 0。有些人甚至在端点±1/2 处根本没有定义,在域上留下两个空洞。我不想卷入这种纷争。这几乎无关紧要,尽管出于某些目的,选择Π(±1/2) = 1/2 最有意义。当出现这种情况时,我们会特殊处理(注:对于离散信号和 Π 的离散版本来说,这实际上是一个更大的问题。这将在第 7 章中出现)。
Π(t)不是周期函数。它没有对应的Fourier级数。在问题中,你尝试过一些周期化(periodizations),我想再次对Π进行这样的周期化扩展。 作为Π(t) 的周期版本,我们以规则的间隔重复函数的非零部分,并以函数为零的(长)间隔分隔函数。我们可以想象,当我们每次打开一个开关并保持一秒钟,并且在两次打开之间我们将其关闭很长一段时间时,重复这样操作,就会出现这样的函数。(人们经常听到与此类事物相关的“占空比(工作周期)(duty cycle)”一词。)下面图2.2是周期为 16 时的Π(t)的函数图像。
-----------------------------------------图2.2. 周期为 16 时的Π(t)的函数图像-------------------------------
以下是周期为 4、16 和 32 的周期化矩形函数的一些Fourier系数函数图;对于这三个周期中的每一个周其,分别对应第 0 个系数,10 个系数、60 个系数和 200 个系数(注:由于 Π 不连续,Fourier系数永远持续下去)。频谱是对称的,并且显示正频率和负频率。 周期函数是实数且偶数,因此在每种情况下Fourier系数都是实数。这些是系数的图,而不是它们的大小。
事实上,不完全是。稍后我将解释水平轴上的缩放,即为什么Fourier系数 ![]() 不仅仅绘制在整数 n 处。还有一个重要的垂直缩放问题。但要记住整体形状——这就是重点。
不仅仅绘制在整数 n 处。还有一个重要的垂直缩放问题。但要记住整体形状——这就是重点。
---------------------------------------图2.3. 周期为 16 时的Π(t)的函数图像----------------------------------------
如图所示,随着周期的增加,频率越来越接近(译注:周期越大,频率越小),看起来系数似乎正在跟踪某些明确的曲线。我们可以分析这个特定示例中发生的情况,并将其与一些一般性陈述相结合来引导我们前进。
回顾一下,具有周期 T 的函数的Fourier 级数具有以下形式
并且其频率是 0,±1/T,±2/T ,... 。频谱中的点分别以1/T 为间隔,事实上,在上面的图片中,随着周期 T 的增加而频谱变得越来越紧密。第 n 项Fourier 系数由公式
![]()
给出。
我们可以计算Π(t)的Fourier 系数:
![]()
----![]()
----![]() 。
。
现在,尽管这个频谱是按 n 索引的,但频率中的点是 n/T (n = 0, ±1,±2,...),将频率信息( ![]() 的值 )看成是函数Π在点 n/T 处取值(evaluated)的一种变换更有帮助(译注:将 (n/T )作为一个整体,看成一个变量)。我们暂且将其写成如下形式:
的值 )看成是函数Π在点 n/T 处取值(evaluated)的一种变换更有帮助(译注:将 (n/T )作为一个整体,看成一个变量)。我们暂且将其写成如下形式:
![]() 。
。
我们几乎触及Fourier变换了,但是还有一点距离。如果你渴望的只不过是取得 T ⟶∞ 时的极限,考虑,对于每一个 n ,若 T 非常大,则 n/T 就非常小,并且
![]() 大致的大小是
大致的大小是 ![]() (记住,当 θ 非常小的时候,sin(θ)≈θ 。)
(记住,当 θ 非常小的时候,sin(θ)≈θ 。)
换句话说,对于每一个 n ,这个所谓的Fourier变换,
![]()
就类似 ![]() ,T 变得非常大时趋近于0 。当T ⟶∞ 时,Fourier系数全部趋近于0 。为了补偿这种缩小的趋势,我们按比例 T将这个缩小的趋势放大,考虑替代形式
,T 变得非常大时趋近于0 。当T ⟶∞ 时,Fourier系数全部趋近于0 。为了补偿这种缩小的趋势,我们按比例 T将这个缩小的趋势放大,考虑替代形式
![]() 。
。
事实上,缩放变换的图就是我上面向您展示的。
接下来,如果 T 非常大,则我们可以考虑用一个连续变量(比如说,s)来替换紧密排列的离散点 n/T ,因此,令 s = n/T , 则我们可以近似地写成
![]() 。
。
根据积分公式,这个例程(procedure)看起来像什么呢?很显然,
![]()
--------------------------------------------------------------------![]()
--------------------------------------------------------------------![]() 。
。
现在,我们将 T ⟶∞ 时产生的效果,看成是与用一个连续变量 s 替换替换紧密排列的离散变量n/T 而产生的效果一样,同时,两种方法都将积分的上下限推向±∞。则我们可以将Π 的(极限)变换写成积分表达式
![]() 。
。
看哪(behold),Fourier变换诞生了! 或者很快就会诞生。为了表示对Fourier系数的敬意我们使用了记法 ![]() ,但是在后面我们还会有更多的记法。
,但是在后面我们还会有更多的记法。
让我们计算积分(我们知道答案是什么,因为我们之前看到了它的离散形式):
![]() 。
。
这是一个图像。您现在肯定可以看到由离散、缩放的傅立叶系数图绘制的连续曲线。
---------------------------------------------图2.4. sin(πs)/πs 函数图像-------------------------------------------
函数 sin(πx)/πx(现在写成通用变量x的形式)在这个主题中出现得如此频繁,因此人们给它取了个专用名 sinc (发音“sink”),
![]() 。
。
注意,借助著名的极限公式
可以求得
sinc(0) = 1 。
毫无疑问,当你学习微积分时,你已经看到了这个极限表达式,并且你可能认为你再也不会看到它了。但 sinc 函数在 EE (译注:电子工程/电气工程)应用和其他地方非常重要,因为它是矩形函数的Fourier变换。 事实上,可以公平地说,许多 EE 都在梦想中看到了 sinc函数。
-------------------------------------图 2.5 生活中的 sinc 函数图像的图案-----------------------------------
Fry电子(Fry's Electronics)是硅谷(Silicon Valley)及其他地区著名的电子产品商店。他们当然了解他们的客户。 我个人尽了自己的一份力量来帮助他们的生意。我在获得Fry电子公司(Fry’s Electronics Inc.)和美国数学研究所(American Institute of Mathematics)的许可下使用这些图片。
2.1.2 变换思想的泛化(In general)
我们想导出同样的思想——按T缩放Fourier系数(如果我们开始对任何函数进行周期化扩展,目的是令周期 T 趋于无穷大)。假如 f(t)在|t|≤1/2之外为0。(任何区间都可以;我们只是想假设函数在某个区间之外为零,这样我们就可以进行周期化扩展。) 我们周期化扩展 f(t) 并使其具有周期 T并计算其Fourier系数:
![]() 。
。
这个系数有多大?我们可以估算:
![]()
------![]()
------![]()
------![]() ,
,
其中,
![]() 。
。
这个 A 是一个独立于 n 和 T 的固定的数,我们再一次看到 ![]() 像 1/T 一样趋近于 0 ,因此,我们再次按 T 放大并考虑
像 1/T 一样趋近于 0 ,因此,我们再次按 T 放大并考虑
![]()
--------------------------------------------------------------------![]()
--------------------------------------------------------------------![]() 。
。
在极限表达式中,当T ⟶∞ 时,我们用 s 替换 n/T 并考虑
![]() 。
。
我们已经回到了同样的积分表达式。
2.1.3 Fourier变换的定义(Fourier transform defined)
现在有了,我们现在将一个函数f (t)的Fourier变换定义为
![]() 。
。
现在,仅将这个表达式当成正式定义;稍后,我们将讨论这样一个积分存在的条件。我们假设 f (t) 是定义在所有实数 t 之上的。我们没有假设 f (t) 在某些区间之外是零,我们并不对其进行周期化扩展。这个定义是通用的。注意:我们并没有“推导(derive)” Fourier变换——我们只是激发了这个定义(we motivated the definition)。
对于任意 s∈ℝ,将 f (t) 与复数值函数 ![]() 针对 t 进行积分,通常产生的也是一个 s 的复数值函数。记住,Fourier变换
针对 t 进行积分,通常产生的也是一个 s 的复数值函数。记住,Fourier变换 ![]() 是一个 s∈ℝ 的复数值函数。由于对称性的原因,存在
是一个 s∈ℝ 的复数值函数。由于对称性的原因,存在 ![]() 是实数的情况(比如,
是实数的情况(比如,![]() ),我们将讨论这个问题。
),我们将讨论这个问题。
周期函数的频谱是一组离散的频率,可能是一个无限的集合(例如,当存在某种阶的不连续性时),但始终是一个离散的集合。 相比之下,非周期信号的傅立叶变换产生连续频谱或连续频率。有可能存在这种情况,对足够大的 |s|,变换 ![]() 都同样等于零(一种称为“带限(bandlimited)”的重要信号类),或者
都同样等于零(一种称为“带限(bandlimited)”的重要信号类),或者 ![]() 的非零值扩展到 ±∞,或者
的非零值扩展到 ±∞,或者 ![]() 的零值仅出现在几个 s 值处。
的零值仅出现在几个 s 值处。
虽然Fourier变换摆脱了以周期函数为模型寻找非周期函数谱信息的愿望,但结果的额外复杂性和额外丰富性很快就会使我们看起来像是处于一个截然不同的世界。刚刚给出的定义是一个很好的定义,因为它既丰富又复杂。 周期函数很棒,但还有很多东西需要分析。
仍然类比于Fourier级数,Fourier变换分析信号 f (t) 是进入到其频率成分 ![]() 我们还没有考虑相应的合成是如何进行的。我们可以如何从频域内的
我们还没有考虑相应的合成是如何进行的。我们可以如何从频域内的 ![]() 将信号恢复为时域内的 f (t) ?
将信号恢复为时域内的 f (t) ?
2.1.3.1 从Fourier变换  恢复原信号f (t) (Recovering f(t) from
恢复原信号f (t) (Recovering f(t) from  )
)
我们可以将非周期函数作为周期函数的极限的想法进一步推进一些,并发现我们可以怎样从其变换 ![]() 恢复原始信号 f (t) 。再次假设 f (t) 在某个区间之外是0 ,并对其进行周期化扩展,使其具有(足够大的)周期 T 。我们按 Fourier级数展开 f (t) ,
恢复原始信号 f (t) 。再次假设 f (t) 在某个区间之外是0 ,并对其进行周期化扩展,使其具有(足够大的)周期 T 。我们按 Fourier级数展开 f (t) ,
我们可以借助 f 的Fourier变换在点 ![]() 处计算出的值来书写Fourier系数:
处计算出的值来书写Fourier系数:
![]()
(我们可以将积分上下限扩展到 ±∞,因为 f (t)在[-T/2,T/2]之外是0 )。
--------------------------------------------![]() 。
。
将 ![]() 的这个表达式插入 f (t) 的表达式:
的这个表达式插入 f (t) 的表达式:
点集 ![]() 分别以 1/T 为间距,因此,我们可以将1/T 视为Δs (比如),并将以上和式视为逼近积分的Riemann和:
分别以 1/T 为间距,因此,我们可以将1/T 视为Δs (比如),并将以上和式视为逼近积分的Riemann和:
![]() 。
。
积分上下限从 –∞ 到 ∞,因为这个和以及点集 ![]() 从–∞ 到 ∞分布。因为,这个周期 T ⟶∞ 时,我们可以预期有
从–∞ 到 ∞分布。因为,这个周期 T ⟶∞ 时,我们可以预期有
![]() ,
,
这样,我们就可以从 ![]()
恢复原始信号 f (t)。我们已经发现了逆Fourier变换(reverse Fourier transform)和Fourier反演(Fourier inversion)。
2.1.3.2 逆Fourier变换和Fourier反演的定义(The inverse Fourier transform defined, and Fourier inversion too)
我们刚刚提出的积分其自身可以独立作为变换(译注:即所谓的“反演”),因此我们将函数 g(s) 的逆Fourier变换定义为
![]() (底向下的帽,很可爱;读作“(勾号)check”)。
(底向下的帽,很可爱;读作“(勾号)check”)。
逆Fourier变换与Fourier变换看起来相似(除了后者在复数指数上有一个“-”号之外)(译注:反演特性)。在后面,我们将讨论更多关于Fourier变换与其逆变换之间的对称性问题。
同样,我们暂时正式处理这个问题,不讨论积分有意义的条件。本着同样的精神,我们还提出了Fourier反演定理,即,
![]() 。
。
这个公式适用于(当应用的时候)常用函数及其Fourier变换。非常精简的写法,
![]() 。
。
顺便说一下,我们可以从 ![]() 而不是 f 开始,完成上面的整个论证。如果我们这样做了,我们就会导出Fourier反演的互补结果
而不是 f 开始,完成上面的整个论证。如果我们这样做了,我们就会导出Fourier反演的互补结果
![]() 。
。
2.1.4 快速总结和展望(A quick summary and a look ahead)
让我们总结一下我们所做的事情,部分是为了修正想法,部分是作为我们下一步要做的事情的指南。涉及的事情太多,都很重要,一切都准备就绪需要一些时间。
![]() 信号 f (t) 的 Fourier变换是
信号 f (t) 的 Fourier变换是
这是变量 s 的复数值函数。
![]()
![]() 的定义域是积分存在的实数s 的积合。有人说
的定义域是积分存在的实数s 的积合。有人说 ![]() 定义在频域(frequency domain)上,而 f (t) 定义在时域(time domain)(或者空间域(spatial domain),取决于背景)上。我们已经开始使用这些术语了。
定义在频域(frequency domain)上,而 f (t) 定义在时域(time domain)(或者空间域(spatial domain),取决于背景)上。我们已经开始使用这些术语了。
对于定义在整个实数轴上的(非周期)信号,我们没有像周期信号情况那样的一组离散频率,而是一个频率的连续区(continuum)(注:周期函数确实有Fourier变换,但它是 δ 函数的和。我们也必须这样做,并且需要付出一些努力)。
与Fourier级数一样,人们通常称 ![]() 的值为频谱。这种混称不应该引起混淆。但它指出了Fourier级数和Fourier变换之间的区别,我将在下面简要讨论。同样,Fourier级数也是如此,我们称复指数
的值为频谱。这种混称不应该引起混淆。但它指出了Fourier级数和Fourier变换之间的区别,我将在下面简要讨论。同样,Fourier级数也是如此,我们称复指数 ![]() 为谐波(harmonics)。
为谐波(harmonics)。
![]() 的一个特殊值值得引起注意;即,对于 s = 0,我们有
的一个特殊值值得引起注意;即,对于 s = 0,我们有
如果f (t) 是实信号,正如在通常应用中最常见的情况一样,则,尽管Fourier变换的其它但可能是复数,但 ![]() 是实数。在积分项中,
是实数。在积分项中, ![]() 是位于f (t)图像之下的面积。
是位于f (t)图像之下的面积。
![]() 逆Fourier变换定义为
逆Fourier变换定义为
Fourier反演指的是,
![]() ,
,![]() 。
。
总而言之,Fourier变换及其逆变换提供了一种在信号的两个(等价)表示之间相互转化(passing)的方式。
借助Fourier变换,函数 f (t) 和 ![]() 可以“等价”,但是它们也有相当不同的属性;比如,一个可能为实数值,而另一个可能为复数值。当
可以“等价”,但是它们也有相当不同的属性;比如,一个可能为实数值,而另一个可能为复数值。当 ![]() 存在时,我们真的可以将它代入Fourier逆变换的公式中(这是一个广义积分(improper integral),除了减号之外,看起来与正变换相同),然后真的可以求得 f (t) 吗? 真的吗? 不明显! 值得人们思考。
存在时,我们真的可以将它代入Fourier逆变换的公式中(这是一个广义积分(improper integral),除了减号之外,看起来与正变换相同),然后真的可以求得 f (t) 吗? 真的吗? 不明显! 值得人们思考。
我们注意到 Fourier逆变换的一个结果,即,
对于这个结果没有快速的微积分解释。右侧是复值函数的积分(通常),结果是实数(如果 f (0)是实数)。
![]() 如果 t 具有time的量纲(dimension),则为了使在指数
如果 t 具有time的量纲(dimension),则为了使在指数 ![]() 中的 st 无量纲,变量 s 必须具有量纲 1/time 的量纲,即,很显然这个量纲是频率。通常,不管
中的 st 无量纲,变量 s 必须具有量纲 1/time 的量纲,即,很显然这个量纲是频率。通常,不管 ![]() 中的变量指的是什么,它们的量纲必须互为倒数(reciprocal)。
中的变量指的是什么,它们的量纲必须互为倒数(reciprocal)。
这是两个域之间互为倒数关系的第一个例子,也是未来许多例子中的第一个。当发生此类关系时,我们会注意到它们。期待它们的发生。他们将帮助您组织对主题的理解。
![]() 平方大小
平方大小 ![]() 称为功率谱(power spectrum)(特别是在其与通信相关的使用中),或者称为光谱功率谱密度(spectral power density) (特别是在其与光学(optics)相关的使用中),或者能量谱(energy spectrum)(特别是在其与其它相关领域的使用中)。
称为功率谱(power spectrum)(特别是在其与通信相关的使用中),或者称为光谱功率谱密度(spectral power density) (特别是在其与光学(optics)相关的使用中),或者能量谱(energy spectrum)(特别是在其与其它相关领域的使用中)。
在时间域的信号能量与频率域的功率谱之间的一种重要关系是Fourier变换的Parseval恒等式(注:这个名称是为了纪念法国数学家Marc-Antoine Parseval。尽管通常在不同的关系中,这个恒等式也称为Plancherel定理)。
这是Rayleigh 恒等式的Fourier变换版本。也是未来的一个具有吸引力的热点主题。
2.1.4.1 关于符号的一条忠告:没有完美;好用为善(A Warning on notations: None is perfect;all are in use)
根据要执行的运算或背景,为Fourier变换提供替代符号是很有用的。但这里有一个忠告,这是抱怨的开始,这是全面咆哮(blown rant)的前奏(prelude)。玩弄符号(Diddling with notations)似乎是这个主题中不可避免的麻烦(hassle)。在变换和其逆变换之间来回翻转,在不同的域中命名变量(甚至写或不写变量),将加号改为减号,取复共轭,这些都是日常的例行运算,如果你不小心,有时即使你很小心,它们也会造成无尽的混乱。当我们有一些例子时你就会相信我说的话,并且你会经常听到我抱怨它。
这儿有一个常用的符号约定的例子:
如果用 f 表示函数,则人们通常用对应的大写字母 F 表示Fourier变换。因此,读者往往会看到 a 和 A,z 和 Z,以及一切大小写成对的表示。然而,要注意,一种典型的用法是对这两个函数使用不同的变量名,例如,f (s)(或f (t))和F(s)。这个“大写字母符号”在工程领域非常普遍,但是在提及对偶性(duality)性时,常常使人困惑,下面将对此进行解释。
原因在于:
由于采用Fourier变换是一种应用于函数以产生新函数的运算,因此有时通过一种运算符号来表示这一点也很方便。例如,
这通常是最明确的表示法。
对于那些相信括号力量的人来说,写成
更合适,表明我们采用 f 的变换,并通过给定的公式在 s 处计算该变换。但额外的括号(可能)是画蛇添足,我们不会使用它们。请注意。
则进行逆Fourier变换使用符号 ![]() 表示,因此,
表示,因此,
Fourier 反演看起来就像,
![]() ,
,![]() 。
。
我们经常会使用符号 ![]() 和
和 ![]() 。这种符号也远非理想,但总体而言它带来的问题较少。
。这种符号也远非理想,但总体而言它带来的问题较少。
最后,一个函数及其Fourier变换称为构成一个Fourier对(pair)。人们设计了多种符号来表示这种兄弟关系。一个是
f (t) ⇌ F(s) 。
Bracewell主张使用
F(s)⊃ f (t) ,
并且其他人也有在使用它。我不喜欢使用这个符号。
2.1.4.2 关于定义的一条忠告(A warning on definitions)
我们对Fourier变换的定义是常见的,但不是唯一的。一个问题是将 2π 放在指数中的什么位置,就像我们所做的那样;或者也许作为一个重要因素;或者也许完全被排除在外。还有一个问题是哪个是Fourier变换,哪个是Fourier逆变换,即哪个变换在指数中得到负号。所有各种惯例都在专业领域中经常使用。在本章的最后,我将总结不同约定下的公式会发生什么情况。我现在才提到这一点,因为当您与朋友谈论Fourier变换时,请确保你们都知道遵循哪些约定。否则友谊因此破裂。
2.1.4.3 关于频谱的一条评述(A comment on spectrum)
对于Fourier级数,只有当这一点 n 对应的Fourier系数 ![]() 时,我们才认为这一点位于频谱中。这是正确的做法,因为在Fourier级数
时,我们才认为这一点位于频谱中。这是正确的做法,因为在Fourier级数
![]()
中,系数为零或非零都会改变信号。
Fourier变换却不是这样。改变某一点或某几点,或者更常见的改变一组零测度(measure zero)的点的 ℱ f (s) 值,并不会影响到借助 Fourier反演从 ℱ f (s)恢复信号 f (t)。在公式
中,改变一组零测度上的 ℱ f (s) 值不会改变积分:它们不会影响积分的值。出于同样的原因,改变一组零测度上的 f 值会使其Fourier变换 ℱ f 保持不变。
什么是零测度集合? 这个问题问得好,但这个问题超出了我们的需要(注:零测度集对于从Riemann积分推广到Lebesgue积分非常重要。第 4.3 节对此有更多讨论。在典型的应用中您不太可能需要担心这些事情)。只要说有限集是零测度就足够了,某些无限集也是如此。
因此,除了一个例外,一个点属于频谱的标准只是Fourier变换存在。一个例外情况是,当 ℱ f (s) = 0 不仅仅是发生在孤立点,而是发生在(比如说)一个(有限的)区间集合上的时候的这种情况。如果在区间 I 上 ℱ f (s) = 0,则
所以我们可以在积分中省略这些区间:
(注:“complement of all such I’s”,即“所有像I这样的补集”。)
换句话说,ℱ f (s) = 0 的区间无助于通过 Fourier 逆变换从 ℱ f (s) 恢复 f (t) 信号,我想说,这些 s 值不在频谱内。
重要的例子是在采样理论中出现的带限信号(bandlimited signals)(在第6章中)(注:或者更笼统地说,是一组正的测度)。这些信号满足
ℱ f (s) = 0 (对于 ![]() ) 。
) 。
我们不认为 ![]() 的点在频谱内(但是是否考虑端点在频谱内存在争议)。
的点在频谱内(但是是否考虑端点在频谱内存在争议)。
我们已经完成了忠告和评述。 转向更有趣的事情。
2.2 理解Fourier变换(Getting to Know Your Fourier Transform)
至少,在某种程度上,我们对Fourier变换的学习将与您对微积分的学习一样,贯穿相同的过程。当你学习微积分时,有必要学习特定函数和函数类型(幂、指数、三角函数——社会需要的函数)的导数和积分公式,并学习微分和积分的一般原理和规则。允许您使用函数组合(乘积法则、链式法则、反函数)。 现在对我们来说也是同样的事情。我们需要拥有一个可以调用的具体函数及其变换的仓库,并且我们需要制定有关Fourier变换如何运行的一般法则和结论。
2.2.1 一些具体的变换(Some specific transforms)
我们已经看到了Fourier变换的例子
![]() 或者
或者 ![]() (采用 ℱ 记法)。(采用 ℱ 记法)。
(采用 ℱ 记法)。(采用 ℱ 记法)。
让我们举更多几个例子。
2.2.1.1 三角形函数的Fourier变换(The triangle function)
接下来考虑三角形函数,定义为
下面是其图像。
----------------------------------------------------图 2.6 函数Λ(x)的图像----------------------------------------------
您在问题 1.7 的周期化中使用了三角形函数及其缩放版本。
其Fourier变换为
这里需要用到分部积分,如果你回顾一下我们在第一章中对三角波的Fourier系数的计算,类似的观察可以为我们节省一些工作。令 A(s)为第一个积分,
则,
作变量替换 u = -x 转化成
因此,
![]() ,
,
------------------![]()
------------------![]()
------------------![]() (使用
(使用 ![]() )
)
-----------------![]() 。
。
棘手!三角形函数的Fourier变换实际上是矩形函数的Fourier变换的平方,这并非偶然。 它与卷积有关,这是我们在Fourier级数中看到的一种运算,并将在下一章中再次在Fourier变换中看到。
![]() 函数的图像如下图所示。
函数的图像如下图所示。
-------------------------------------------------图 2.7 ![]() 的图像----------------------------------------
的图像----------------------------------------
2.2.1.2 指数递降函数的Fourier变换(The exponential decay)
另一个经常出现的函数是单侧指数递降函数,定义为
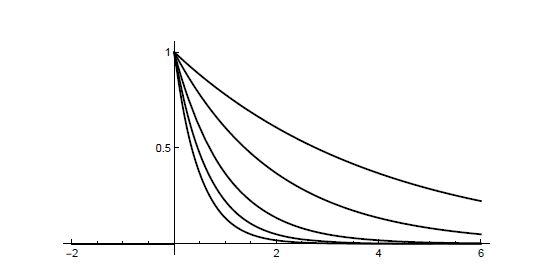
其中,a 是一个正常数。该函数对一个信号为零、打开、然后呈指数递降的信号进行建模。下面是 a 分别等于 2,1.5,1,0.5,0.25 时的图像。
--------------图 2.8 指数递降函数f (t)在a 分别等于 2,1.5,1,0.5,0.25 时的图像--------------------
哪个是哪个?如果你不能区分,请参阅本节末尾关于缩放自变量的讨论。
回到指数递降,我们可以直接计算它的Fourier变换:
--------------------------------------------![]()
--------------------------------------------![]()
--------------------------------------------![]()
--------------------------------------------![]() 。
。
在这种情况下,与矩形函数和三角形函数的结果不同,Fourier变换很复杂。ℱf (s) 和 ℱΛ(s) 都是实信号是因为Π(x)和Λ(x)都是偶函数;我们很快就会讨论(go over)这个问题。 指数递降函数不存在这样的对称性。
这个指数递降函数的功率谱是
![]() 。
。
以下是与指数递降函数图中相同的 a 值时该函数的图。
----------------------------------图2.9 与图2.8中相同a值对应的Fourier变换图-------------------------------
哪个是哪个?您很快就会学会立即发现相对于时域图片中对应的频域图,这很重要。此外请注意,虽然 ℱf (s) 不是偶函数,但 ![]() 是一个偶函数。我们将会看到为什么后者是偶函数。
是一个偶函数。我们将会看到为什么后者是偶函数。![]() 的形状是钟形曲线(a bell curve),尽管这不是一个Gauss曲线,我们将在下面讨论这个函数。这个曲线称为Lorentz 剖面(Lorentz profile)(注:以荷兰物理学家 H. Lorentz的名字命名。他因在电动力学和(在其如此命名之前)狭义相对论方面的工作而闻名。您可能遇到过Lorentz收缩(Lorentz contraction))并在分析原子中激发态的跃迁概率和寿命时出现。
的形状是钟形曲线(a bell curve),尽管这不是一个Gauss曲线,我们将在下面讨论这个函数。这个曲线称为Lorentz 剖面(Lorentz profile)(注:以荷兰物理学家 H. Lorentz的名字命名。他因在电动力学和(在其如此命名之前)狭义相对论方面的工作而闻名。您可能遇到过Lorentz收缩(Lorentz contraction))并在分析原子中激发态的跃迁概率和寿命时出现。
2.2.1.3 如何对比分析f(ax)和f(x)的图像(How does the graph of f(ax) compare with the graph of f(x)?)
让我提醒您一些有关缩放函数中自变量的基本知识。问题在于当 0 < a < 1 和 a > 1 时,如何比较分析 f (ax) 与 f (x) 的图像;我在这里讨论的是任何泛型(generic)函数 f (x)。这非常简单,特别是与我们已经做过的和我们将要做的相比,但你会希望它触手可及,每个人都必须考虑几秒钟。以下是如何度过这几秒钟的方法。
例如,考虑 f (2x) 的图像。f (2x) 的图像与 f (x) 的图相比,被挤压了。为什么? 想象一下,当您在 −1 ≤ x ≤ 1 上绘制 f (2x) 的图形时会发生什么。当 x 从 −1 变为 1 时,2 x 从 −2 变为 2,因此当您绘制 f (2x) 在从 -1 到 1 的区间内,您必须计算从 -2 到 2 的 f (x) 值。可以说,在更小的空间中可以实现更多的函数,因此 f (2x) 的图形为 f (x) 图的压缩版本。很清楚了吧?
类似的推理表明 f (x/2) 的图形被拉伸。 如果 x 从 -1 到 1,则 x /2 从 -1/2 到 1/2,因此当您在区间 -1 到 1 上绘制 f (x/2) 时,您必须计算从 −1/2 到 1/2这些值 f (x)。 这是在更大空间中的函数更少,因此 f (x/2) 的图是 f (x) 图的拉伸版本。
2.2.2 钟形曲线为谁而“鸣”(For Whom the Bell Curve Tolls)
接下来让我们考虑Gauss函数及其Fourier变换。对于许多示例和问题,我们都需要它。这个函数,即著名的钟形曲线,被Gauss用来解决统计问题。相对于Fourier变换,它具有一些显着的特性,一方面,赋予它在Fourier分析中的特殊作用,另一方面,允许Fourier方法应用于该函数出现的其他领域。我们将在第 3 章中看到概率的应用。
基本的Gauss函数是 ![]() 。这个图像的形状是您所熟悉的:
。这个图像的形状是您所熟悉的:
----------------------------------图 2.10 Gauss函数 ![]() 的图像-------------------------------
的图像-------------------------------
对于各种应用,我们可以添加额外的因素来修改函数的特定属性。我们也会这样做,但对于什么是最好的还没有完全一致。大家一致认为,在发生任何其他事情之前,我们必须知道这个令人惊奇的方程式(注:William Thomson 在成为Kelvin勋爵(Lord Kelvin)后,谈到这个方程式时说道:“对数学家来说,这个方程式对你而言就像二乘二等于四一样显而易见。” 我想他是在开玩笑):
请注意,函数 ![]() 没有初等的反导数,因此不能通过诉诸微积分基本定理直接求得该积分。事实上,它可以被精确地估算,这是数学中最著名的技巧之一。这是Euler的功劳,你不应该在没有看到它的情况下度过一生。即使你看过,也值得再看一遍;请参阅本节后面的讨论。首先是Fourier变换。
没有初等的反导数,因此不能通过诉诸微积分基本定理直接求得该积分。事实上,它可以被精确地估算,这是数学中最著名的技巧之一。这是Euler的功劳,你不应该在没有看到它的情况下度过一生。即使你看过,也值得再看一遍;请参阅本节后面的讨论。首先是Fourier变换。
2.2.2.1 Gauss函数的Fourier变换(The Fourier transform of a Gaussian)
无论应用于什么主题,对Gauss函数进行归一化(normalize)以使总面积为 1 似乎总是有用的。这可以通过多种方式完成,但对于Fourier分析来说,最好的选择(我们将看到)是
![]() 。
。
你可以使用 ![]() 和积分结果来检验(
和积分结果来检验( ![]() 的积分结果)
的积分结果)
我们来计算其Fourier变换,
针对 s 对等式两侧进行微分:
因此,ℱf (s)满足简单的微分方程
![]() ,
,
其包含初始条件的唯一解是
![]() 。
。
但是,
因此,
![]() 。
。
我们已经发现了这个明显的事实,Gauss函数 ![]() 是其自身的Fourier变换。
是其自身的Fourier变换。
2.2.2.2 计算Gauss积分(Evaluation of the Gaussian integral)
我们希望计算
我们使用什么名称作为积分变量都没有关系,因此,我们也可以将积分写成
因此,
![]() 。
。
现在我们做变量替换,引入极坐标 (r ,θ) 。首先,积分的上下限是什么样?令 x 和 y 从 –∞ 到 ∞ 分布是为了描述整个平面,在极坐标平面中,要描述整个平面需要令 r 从 0 贯穿到 ∞ ,并令θ 从 0 贯穿到 2π。接下来,![]() 就转换成了
就转换成了 ![]() ,面积元素转换了 r dr dθ 。正是这是面积元素中额外因子 r 造成了所有的差异。根据这个到极坐标的变换方法,我们有
,面积元素转换了 r dr dθ 。正是这是面积元素中额外因子 r 造成了所有的差异。根据这个到极坐标的变换方法,我们有
![]() 。
。
由于这个因子 r 的原因,可以直接对这个内部积分进行积分:
![]() 。
。
则这个双重积分即简化为
![]() 。
。
因此可得,
![]() 。
。
完美!
2.2.2.3 关于例子的补充说明(A final word on the examples)
您可能已经注意到,到目前为止我们的列表并未包括社会所需的许多基本函数。例如,正弦和余弦还没有出现,你无法得到比这更基础的函数了。这还得等。没有办法从经典角度理解积分
需要采用完全不同的方法去理解。
尽管如此,还有更多的例子可以做。你可以在网上找到关于这些例子的汇编,另外,Bracewell的书中有一段非常吸引人的“Fourier变换图解词典”。
2.3 更进一步理解Fourier变换(Getting to Know Your Fourier Transform, Better)
我们已经开始构建特定转换的仓库。现在让我们沿着另一条路径继续前进一段时间并开发一些通用属性。对于本次讨论,以及接下来的许多页中的大部分工作,我们将放弃所有关于现有变换、积分收敛以及您可能携带的任何其他担忧的担忧。放松并享受旅程。严谨的警察已经下班了。
2.3.1 Fourier变换对与对偶性(Fourier transform pairs and duality)
Fourier变换和逆Fourier变换的一个显著特征是两个公式之间的对称性,这是Fourier级数所看不到的。对于Fourier级数,系数由积分给出( f (t ) 到 ![]() 的一种变换),但逆变换是级数本身。对于Fourier变换,除了复指数中的负号之外,
的一种变换),但逆变换是级数本身。对于Fourier变换,除了复指数中的负号之外, ![]() 和
和 ![]() 看起来相同(注:这就是Fourier变换及其逆变换的公式显得如此对称的原因;这是一个相当深刻的数学事实。按照一般理论,如果原函数是在群上定义的,那么变换(也是一般性定义的)是在对偶群上定义的,这里我就不给大家定义了。对于Fourier级数,函数是周期性的,因此它的自然域是圆;将圆视为端点相等的函数的区间[0, 1],并且群的的元素是圆的旋转。事实证明,圆群的对偶是整数,这就是为什么
看起来相同(注:这就是Fourier变换及其逆变换的公式显得如此对称的原因;这是一个相当深刻的数学事实。按照一般理论,如果原函数是在群上定义的,那么变换(也是一般性定义的)是在对偶群上定义的,这里我就不给大家定义了。对于Fourier级数,函数是周期性的,因此它的自然域是圆;将圆视为端点相等的函数的区间[0, 1],并且群的的元素是圆的旋转。事实证明,圆群的对偶是整数,这就是为什么 ![]() 在整数 n 处计算的原因。结果还表明,当群是ℝ (加法下的群)时,对偶群又是 ℝ。因此,在 ℝ 上定义的函数的Fourier变换本身也在 ℝ 上定义。在这种情况下,通过Fourier变换及其逆变换的一般定义,可以得到我们面前的对称结果)。换句话说,我们可以说,如果在Fourier变换的公式中将 s 替换为 -s,那么您将得到Fourier逆变换。同样,如果在Fourier逆变换公式中将 t 替换为 -t,那么您就进行了Fourier变换。即,
在整数 n 处计算的原因。结果还表明,当群是ℝ (加法下的群)时,对偶群又是 ℝ。因此,在 ℝ 上定义的函数的Fourier变换本身也在 ℝ 上定义。在这种情况下,通过Fourier变换及其逆变换的一般定义,可以得到我们面前的对称结果)。换句话说,我们可以说,如果在Fourier变换的公式中将 s 替换为 -s,那么您将得到Fourier逆变换。同样,如果在Fourier逆变换公式中将 t 替换为 -t,那么您就进行了Fourier变换。即,
这可能会引起一些恐慌,因为您通常希望将 s 和 t 这两个变量视为与单独且不同的域相关的某种方式,一个域用于正向变换,一个域用于逆变换,一个域用于时间,一个域用于频率, 而在每个公式中,两个域都使用一个变量。你必须克服这种惊愕,因为它还会再次出现。纯粹从数学角度思考:变换是对函数的运算,产生一个新函数。为了写下公式,我必须计算变量处的变换,但该变量只是一个占位符,只要我保持其在公式中的角色正确,我叫它什么并不重要。
还要注意公式中的符号所说的内容,以及同样重要的,它没有说的内容。例如,第一个公式说明了当您首先对 f 进行Fourier变换,然后在 - s 处对其求值时会发生什么; 它不是 ℱ( f (−s)) 的公式,如“首先将 f 公式中的 s 更改为 − s,然后进行变换”。我可以将第一个显示的方程写为 (ℱ f )(− s) = F-1![]() f (s),并在 ℱ f 周围加上一组额外的括号来强调这一点,但我认为这看起来太笨拙了。这句话再怎么说也不为过:请小心。
f (s),并在 ℱ f 周围加上一组额外的括号来强调这一点,但我认为这看起来太笨拙了。这句话再怎么说也不为过:请小心。
等式
![]() ,
,
![]()
有时候称为变换的对偶(duality)属性。它们看起来像是不同的表述,但您可以从其中一种推导出另一种。我们将在下一节中对其进行稍微不同的设置。
下面是一个如何使用对偶的例子。我们知道,
ℱΠ = sinc 。
因此,
![]() 。
。
根据对象性,我们可以求得
![]() 。
。
因变量而烦恼?记住,左边是 (ℱ sinc)(t) 。现在有了Π 是偶函数 (Π(-t) = Π(t))的额外知识,我们可以得出结论:
ℱ sinc = Π 。
让我们将同样的论证用于求 ![]() 。回顾这个三角形函数 Λ 和结论
。回顾这个三角形函数 Λ 和结论
![]() ,
,
因此,
![]() 。
。
但是,
![]()
且因为Λ是偶函数,
![]() 。
。
2.3.1.1对偶性与反转信号(Duality and reversed signals)
我更喜欢对对偶性的持一种稍微不同的看法,因为它抑制了变量。我发现这样更容易记住。以一个信号 f ( t)开始,将其反转信号 ![]() 定义为
定义为
![]() 。
。
注意,二次反转就回到了原来的信号,
![]() 。
。
另请注意,定义函数为偶函数或奇函数的条件很容易用反转信号来写:
f 是偶函数(若 ![]() )
)
f 是奇函数(若 ![]() )
)
换句话说,如果反转信号不会改变信号,则信号是偶函数;如果反转信号改变其符号,则信号是奇函数。我们将在下一节中讨论这一点。
足够简单——反转信号就是反转时间。无论信号的性质如何以及变量是否是时间,这都是通用操作。使用这个符号,我们可以将第一个对偶方程 ![]() 重写为
重写为
![]() ,
,
同样,将第二个对偶方程 ![]() 重写为
重写为
![]() 。
。
这非常清楚地表明这两个方程说的是同一件事。 其中一个正好与另一个相反。
此外,使用这种表示法,例如,结论 ℱ sinc = Π,会得出得更快些:
![]() 。
。
同样,
![]() 。
。
基于前面的对偶结论的一个自然的变体是 ![]() ,即,反转信号的Fourier变换。我们来计算它。根据定义,
,即,反转信号的Fourier变换。我们来计算它。根据定义,
![]() 。
。
此时只有一件事要做,而且我们会做很多事情:更改积分中的变量。令 u = -t ,因此,du = -dt ,或者 dt = - du 。则随着 t 从 -∞ 到 ∞ ,变量 –t 从 ∞ 到 -∞ ,我们有
![]()
---------------------------------------------![]() (du 上的减号将积分上下限翻转回来)
(du 上的减号将积分上下限翻转回来)
---------------------------------------------![]()
因此,相当简洁,
![]() 。
。
特别注意这里括号的位置。换句话说:
![]() 反转信号的Fourier变换是信号的逆Fourier变换。
反转信号的Fourier变换是信号的逆Fourier变换。
这是我可以很容易理解记忆的。
为了完全弄清楚这些问题,我必须知道 ![]() 发生了什么。但这里我们不必单独计算。使用我们之前的对偶结论,
发生了什么。但这里我们不必单独计算。使用我们之前的对偶结论,
![]() 。
。
换句话说,反转信号的Fourier逆变换就是信号的Fourier逆变换的反转。我们还可以更进一步,回到 ![]() 。
。
因此,到目前为止,对偶关系的列表可以归结为:
![]() ,
,
![]() 。
。
了解这些之后,还有另一个:
![]() 或者不带变量
或者不带变量 ![]() 。
。
这可以从Fourier反演推出:
![]() 。
。
通常删除一组括号并将结果写为:
![]() 。
。
当然,我们也可以写成这样:
![]() 。
。
基于此和之前的对偶结果,您可以检验
![]() ,
,
写为
![]() ,不是 ℱ 的4次幂,而是应用 ℱ 4次。因此,
,不是 ℱ 的4次幂,而是应用 ℱ 4次。因此, ![]() 是恒等变换。有些人赋予这一事实神秘的意义。
是恒等变换。有些人赋予这一事实神秘的意义。
![]() 的一个实际例子是 ℱ sinc = Π 的又一推导,为
的一个实际例子是 ℱ sinc = Π 的又一推导,为
![]() 。
。
2.3.1.2 奇偶对称和Fourier变换(Even and odd symmetries and the Fourier transform)
我们已经在很多场合使用过函数的偶对称性和奇对称性。对于实值函数,根据图形的对称性,对对称条件有明显的解释;偶函数的图形关于 y 轴对称,奇函数的图形关于原点对称。然而,偶函数数和奇函数的代数定义既适用于复值函数,也适用于实值函数,尽管当函数为复值时,由于我们无法绘制图形而缺乏几何图像。一个函数可以是偶函数、奇函数或两者都不是,但它不能既是偶函数又是奇函数,除非它全为零。
函数的对称性如何反映在其Fourier变换的属性中? 我不会给出完整的解释,但这里有几个重要的案例。
![]() 如果 f (x) 分别是偶函数或奇函数,则其Fourier变换也是如此。
如果 f (x) 分别是偶函数或奇函数,则其Fourier变换也是如此。
当使用反转信号的时候,我们必须证明,如果 f 是偶函数, ![]() ,如果 f 是奇函数,
,如果 f 是奇函数, ![]()
![]() 。使用我们上面推导的方程,速度很快:
。使用我们上面推导的方程,速度很快:
。
因为函数的Fourier变换是复数值,我们就可以考虑,对于 ℱf(s)存在其它的对称性,即,在复共轭下发生的事。比如这个:
![]() 如果 f (t) 是实数值,则
如果 f (t) 是实数值,则 ![]() 和
和 ![]() 。
。
这里,值得将变量带回,
![]() 。
。
特别是,
| ℱ f (-s)| = | ℱ f (s)| 。
对于实值信号,Fourier变换的幅度在相应的正频率和负频率处是相同的。这种情况经常出现,类似于实值周期函数的Fourier系数所具有的共轭对称性。
该推导本质上与Fourier系数的推导相同,但在实践中重复它并查看相似之处可能会有所帮助:
-------------![]() (
(![]() ,因为 f (t)是实数,
,因为 f (t)是实数, ![]() )
)
-------------![]() 。
。
如果函数 f (t) 本身具有对称性,我们可以对其进行改进。 例如,结合前面的结果,并记住,如果复数等于其共轭,则该复数是实数;如果等于减去其共轭,则复数是纯虚数。然后我们有:
![]() 如果 f 为实函数且为偶函数,则其Fourier变换也是实函数且为偶函数。
如果 f 为实函数且为偶函数,则其Fourier变换也是实函数且为偶函数。
![]() 如果 f 为实函数且为奇函数,则其Fourier变换是纯虚函数且为奇函数。
如果 f 为实函数且为奇函数,则其Fourier变换是纯虚函数且为奇函数。
我们看到了矩形函数 Π(t) 和三角形函数 Λ(t) 的Fourier变换的第一点。这两个函数都是偶函数,并且它们的Fourier变换和 ![]() 分别是偶函数和实函数。幸好事情就这样解决了。
分别是偶函数和实函数。幸好事情就这样解决了。
2.3.2 Fourier变换的线性特性(Linearity)
Fourier变换最简单且最常被调用的属性之一是它是线性特性(在函数上的运算是线性的)。这意味着
ℱ( f + g)( s) = ℱ f ( s ) + ℱ g( s) ,
ℱ( αf )( s) = α ℱ f ( s) (对于任意α ,实数或复数)。
对于 ![]() ,Fourier变换的线性特性也成立。
,Fourier变换的线性特性也成立。
当我们在讨论奇函数及其变换时,当我们写成 ℱ(−f ) = − ℱ f 时,我们使用了(不加注释)倍数的性质。我敢打赌,我们还没有正式指出这个属性,您不会感到困扰。
2.3.3 Fourier变换的平移定理(Shift theorem)
变量 t 的平移(时间延迟)对Fourier变换有简单的影响。我们期望Fourier变换 | ℱ f ( s)| 的幅度保持不变,因为在时间上平移原始信号不应改变频谱中任何点的能量。因此,唯一的变化应该是 ℱ f ( s) 的相位(译注:初始位置),而这正是发生的情况。
对于一个常量 b,为了计算 f ( t - b)的Fourier变换,我们有
![]() (替换成 u = t – b ;积分上下限仍然是从 -∞ 到 ∞ )
(替换成 u = t – b ;积分上下限仍然是从 -∞ 到 ∞ )
----------------------------------![]() (
(![]() 移到积分之外,因为它不依赖于u )
移到积分之外,因为它不依赖于u )
----------------------------------![]() 。
。
体现这个属性的最佳符号可能是成对符号 ⇌ (注:然而,这是抱怨符号问题的绝佳机会。写 ℱ f ( t - b)会引起我们中一些人在改变符号时同样的焦虑。正在转变什么?正在插入什么? 没有空间写s。 帽子符号表示法更糟糕——再次没有地方可以容纳 s,你真的想用这么宽的帽子来写 ![]() 吗?) 因此:
吗?) 因此:
![]() 如果 f ( t )⇌ F( s) ,则
如果 f ( t )⇌ F( s) ,则 ![]() 。
。
请注意,正如所承诺的那样,Fourier变换的幅度在时移下没有改变,因为前面的因子的幅度为 1:
![]() 。
。
逆Fourier变换的平移定理如下所示:
![]() 如果 F( s) ⇌ f ( t ),则
如果 F( s) ⇌ f ( t ),则 ![]() 。
。
你可以从 ![]() 的积分定义式或者对偶性推导出这个关系。
的积分定义式或者对偶性推导出这个关系。
2.3.4 Fourier变换的调制定理(Modulation theorem)
平移定理的第一个表亲是调制定理,它指出:
![]() 如果 f ( t )⇌ F( s) ,则
如果 f ( t )⇌ F( s) ,则 ![]() 。
。
换句话说,时间上的相位变化对应于频率上的偏移。这是频谱的调制。
改变时间相位的一个实值版本是:
![]() 如果 f ( t )⇌ F( s) ,则
如果 f ( t )⇌ F( s) ,则 ![]() 。
。
我将把这些作为练习。
对于逆Fourier变换:
![]() 如果 F( s) ⇌ f ( t ),则
如果 F( s) ⇌ f ( t ),则 ![]() 。
。
![]() 如果 F( s) ⇌ f ( t ), 则
如果 F( s) ⇌ f ( t ), 则 ![]() 。
。
2.3.5 Fourier变换的伸缩(相似性)定理(Stretch (similarity) theorem)
如果我们在时域中拉伸或收缩变量,Fourier变换会如何变化? 如果我们将 t 缩放到 at,f ( at ) 的Fourier变换会发生什么?
我们假设 a ≠ 0,首先假设 a > 0 。则
(替换为 u = at ;因为 a > 0 , 积分上下限保持不变)
------------------------------------![]() 。
。
若 a < 0 ,当我们做变量替换 u = at 时,积分上下限反转:
------------------------------![]() (引入负号,翻转积分上下限回到原状)
(引入负号,翻转积分上下限回到原状)
-----------------------------![]() 。
。
当 a 是负值(-a = |a|)的时候,-a 是正值,我们可以结合这两种情况并充分展示伸缩定理:
![]() 如果 f ( t )⇌ F( s) ,则
如果 f ( t )⇌ F( s) ,则 ![]() 。
。
这有时也称为相似性定理(similarity theorem),因为将变量从 x 更改为 ax(作为尺度的变)也称为相似性。
逆Fourier变换的结论看起来也一样:
![]() 如果 F (s )⇌ f (t) ,则
如果 F (s )⇌ f (t) ,则 ![]() 。
。
一些重要的观察结果与伸缩定理相关。首先,这显然又是两个域之间的相互关系。
我们多说两句,我们就拿a是正值来说,这是最常见的情况。如果 a 很大(至少大于 1),则与 f (t) 相比,f (a t) 的图形会被水平挤压。频域中正在发生一些不同的事情,实际上以两种方式发生。Fourier变换为(1/a) ℱ (s/a)。如果 a 很大,则与 ℱ (s) 相比,ℱ (s/a) 会被拉伸,而不是被挤压。此外,乘以 1/a,因为变换为 (1/a) ℱ (a/ s) ,也会压缩变换的值。如果 a 很小(小于 1),则会发生相反的情况。在这种情况下,与 f (t) 相比,f (a t) 的图形会水平拉伸,而Fourier变换会水平压缩并垂直拉伸。
总而言之,在时域中延伸的函数在频域中被压缩,反之亦然(注:如果 a < 0,这是同样的现象,但还有一个额外的逆转。读者自己思考一下这件事)。经常用来描述这种现象的短语是信号不能在两种情况下局部化(localized)(即集中在一个点)时域和频域。我们将看到这一原则的更精确表述(注:事实上,量子力学中著名的Heisenberg不确定性原理就是一个例子)。
这有点类似于长周期或短周期的周期函数谱所发生的情况。假设周期为 T,请记住频谱中的点间隔为 1/ T,这一事实我们已使用过多次。 如果 T 很大,那么可以合理地认为该函数在时域中延伸——它会经过很长一段时间才重复下一个周期。但由于 1/ T 很小,频谱就会受到挤压。另一方面,如果 T 很小,那么函数在时域中会被压缩(它在重复之前只经过很短的时间),而频谱会延伸,因为 1/T 很大。
特别注意!在上面的讨论中,我试图不提及变换图的属性术语——尽管您可能条件反射地思考了这些术语,而我稍微涉及了一点——因为变换通常是复数值的。通过查看时域中的 f (t) 图形(如果 f (t) 为实数)和Fourier变换 | ℱf (s)| 的幅度,您确实可以在几何上看到这种在频域中被挤压和延展的现象(注:我们在单边指数递降及其Fourier变换中观察到了这一点,现在您应该返回到该示例并匹配 | ℱf | 的图形与参数的各种值)。
2.3.5.1 举例:缩放矩形函数(Example:The stretched rect)
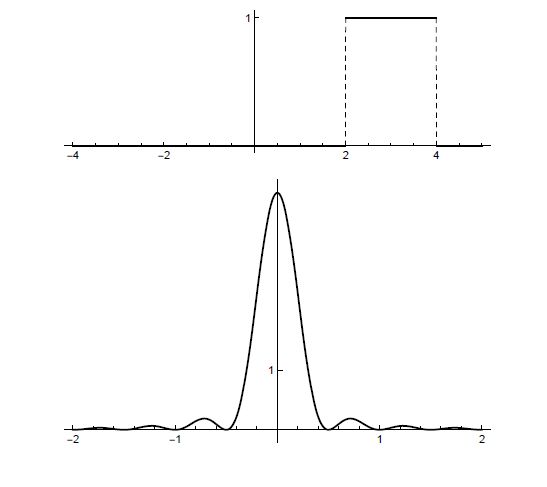
“缩放矩形函数(stretched rect)”并不是一个精当的短语,但该函数在应用中经常出现。令 p > 0 并定义
因此, ![]() 是一个宽度为 p 的矩形函数。我们可以通过直接积分求得它的Fourier变换,但如果我们观察到,我们也可以通过伸缩定理求得它:
是一个宽度为 p 的矩形函数。我们可以通过直接积分求得它的Fourier变换,但如果我们观察到,我们也可以通过伸缩定理求得它:
![]() 。
。
为了确定起见,写下Π的定义并遵循:
。
将伸缩定理应用到 Π(t/p) 我们有
![]() 。
。
这个经常出现,足以记住。
以下分别是 p = 1/5 和 p = 5 时的Fourier变换对的图。注意轴上的刻度。
------------------------图 2.11 ![]() 分别在p = 1/5 和 p = 5 时的Fourier变换对的图-----------------
分别在p = 1/5 和 p = 5 时的Fourier变换对的图-----------------
2.3.5.2 举例:缩放三角开函数(Example:Stretched triangle)
让我们引入缩放三角形函数及其Fourier变换;这些同样会经常出现。对于 p > 0 ,令
注意,这个三角形函数的宽度是 2p 。
下图是 ![]() 在 p = 0.5,1,5 时的图像。
在 p = 0.5,1,5 时的图像。
---------------------------------图 2.12 ![]() 在 p = 0.5,1,5 时的图像------------------------------------
在 p = 0.5,1,5 时的图像------------------------------------
将伸缩定理应用到Λ(t/p)我们得到
![]() 。
。
再次,值得记住。
这是相应的Fourier变换的图。找到对应的曲线图!
----------------------------图 2.13 ![]() 在 p = 0.5,1,5 时的Fourier变换图像-------------------------
在 p = 0.5,1,5 时的Fourier变换图像-------------------------
2.3.5.3 举例:双侧指数递降函数(Example:Two-sided exponential decay)
下面是一个示例,说明如何结合我们开发的属性来求得另一个常见信号的变换。让我们求得双侧指数递降函数的Fourier变换,
![]() (a是一个正常量) 。
(a是一个正常量) 。
下面是 a = 0.5,1,2 时的 g(t)片段图。
------------------------------------图 2.14 g(t) 在 p = 0.5,1,5 时的片段图--------------------------------
我们可以直接计算变换; 代入Fourier变换的公式将为我们提供我们可以做的积分。 然而,当我们求得单侧指数递降函数的Fourier变换时,我们已经完成了一半的工作。 回顾
现在认识到,g(t) 几乎等于 f (t) + f (-t) 。
它们在除了原点处之外一致,其中 g(0) = 1 且 f (t) 和 f (−t) 均为 1 。但是,当对 ![]() 积分(注:例如,请参阅早期关于如何定义频谱的评论)时,除一点外一致的两个函数显然会给出相同的结果。因此,
积分(注:例如,请参阅早期关于如何定义频谱的评论)时,除一点外一致的两个函数显然会给出相同的结果。因此,
![]()
请注意,g(t) 是偶数,G(s) 是实数。 当您进行计算时,这些对正确性和一致性(均匀性、奇数、实数或纯虚数等)的快速检查非常有用。以下是 a = 0.5, 1, 2 的 G(s)的图像。将它们匹配!
--------------------------------------图 2.15 G(s) 在 p = 0.5,1,5 时频谱的片段图--------------------------
接下来,我们将看到双侧指数递降在求解二阶常微分方程中的应用。
2.3.5.4 举例:其它Gauss函数(Other Gaussians)
如前所述,存在归一化Gauss函数的其它方式。例如,替代 ![]() ,我们可以采用
,我们可以采用
您可能从概率到统计的应用中认识到了这一点,它在这些领域作为均值(mean)为零和标准偏差(standard deviation) 为σ(或方差为 ![]() )的Gauss分布。具有均值μ和标准偏差 σ的Gauss函数是 g(x) 的平移版本:
)的Gauss分布。具有均值μ和标准偏差 σ的Gauss函数是 g(x) 的平移版本:
从几何角度来看,σ 是曲线相对于均值的峰值或分布程度的度量。从图中来看,拐点出现在μ±σ处; 因此,如果 σ 较大,则曲线会展开,如果 σ 较小,则曲线会急剧出现峰值。图下的面积仍然是 1。在下一章讨论中心极限定理时,我们将再次遇到Gauss函数。
我们面临的问题是,当以这种方式修改Gauss函数时,Fourier变换会发生什么。这可以通过平移和伸缩的结果来回答。为简单起见,以 μ = 0 为例。 为了求得Fourier变换,我们可以应用相似性定理:f (ax) ⇌ (1/|a|)F(s/a),并且 ![]() ,给出
,给出
仍然是Gauss分布,但不是我们开始时的精确复制品。请注意,当 μ = 0 时,Gauss函数是偶函数,Fourier变换是实数且偶函数。
2.3.6 Fourier变换的平移算子和伸缩算子(The shift operator and the scaling operator)
有时,将移位和缩放视为对信号的运算是有帮助的。我们定义对信号 f(x) 进行运算的延时算子(delay operator)、移位算子(shift operator),或平移算子(translation operator)![]() 为
为
![]() ,
,
( τ 表示“平移”)。
我们定义伸缩算子(scaling operator),或者缩放算子(stretch operator) ![]() 为
为
![]() ,
,
( σ表示“伸缩”)(注:这与上面的标准差σ无关。抱歉,只有这么多字母可用)。你也可以用系统的术语思考,其中,输入是一个信号 f(x) ,输出是延时信号 ![]() ,或者伸缩信号
,或者伸缩信号 ![]() (注:不要太古板,但你可以写成
(注:不要太古板,但你可以写成 ![]() ,
,![]() ,括号的位置表明您正在对信号 f 进行操作并根据公式计算 x 处的结果。就像写成 (ℱ f )(s) 而不是只写 ℱ f (s) 一样)。
,括号的位置表明您正在对信号 f 进行操作并根据公式计算 x 处的结果。就像写成 (ℱ f )(s) 而不是只写 ℱ f (s) 一样)。
如果不出意外的话,引入这些运算符可能可以更清晰地表述移位定理和伸缩定理,即变量上的冲突更少:
![]() ,
,
![]() 。
。
我们甚至可以将伸缩定理更进一步,写成
![]() ,
,
这样做可以让我们完全抑制 s 变量,如果你喜欢这样的事情:
![]() 。
。
对于逆Fourier变换,
![]() 。
。
根据 ![]() ,
,![]() 的伸缩定理只不过是交换
的伸缩定理只不过是交换 ![]() 和
和 ![]() 。
。
当平移和缩放结合在一起时,混乱常常占主导地位——我已经看到了这一点。例如 ![]() 相对于
相对于 ![]() 。
。
这两种情况并不一样,接下来,我们慢慢来分析它。
2.3.6.1 组合平移和伸缩(Combining shifts and stretches)
我们可以结合平移定理和伸缩定理来求得 f (ax - b) 的Fourier变换公式,但让我们准备一个例子。
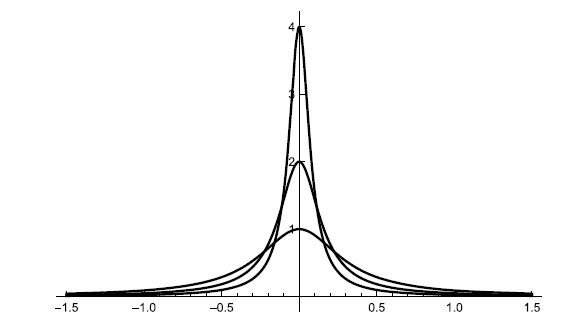
根据直接积分,很容易求得函数 ![]() 的Fourier变换。仅当 2 < t < 4 时,平移、缩放的矩形函数才非零,因此,
的Fourier变换。仅当 2 < t < 4 时,平移、缩放的矩形函数才非零,因此,
![]()
我们仍然可以引入 sinc 函数,但因式分解有点棘手:
![]() 。
。
回顾这一点是这个例子的重点的一部分。 插入给出
![]() 。
。
Fourier变换已经成了复数,因为平移这个矩形函数已经破坏了其对称性。
下面是函数Π((x-3)/2)及其Fourier变换的大小的平方 ![]() 的片段图。再一次,查看后者并不能提供有关频谱中相位的信息,只能提供有关能量的信息。
的片段图。再一次,查看后者并不能提供有关频谱中相位的信息,只能提供有关能量的信息。
-----------图 2.16 函数Π((x-3)/2)及其Fourier变换的大小的平方 ![]() 的片段图---------------------
的片段图---------------------
现在我们来做一下一般公式。 对于 f (ax - b) 的Fourier变换,只需在Fourier变换积分中进行替换即可。我们现在已经习惯了这一点,所以我们不再详细说明:
---------------------------------------------![]()
---------------------------------------------![]() 。
。
其完整特性:
![]() 如果 f ( x )⇌ ℱ( s) ,则
如果 f ( x )⇌ ℱ( s) ,则 ![]() 。
。
在 ![]() 上验证一下。当 a = 1/2 且 b = 3/2 时,我们得到
上验证一下。当 a = 1/2 且 b = 3/2 时,我们得到
![]() 。
。
与之前一样。
对于 ![]()
![]() 如果 F (s )⇌ f (x) ,则
如果 F (s )⇌ f (x) ,则 ![]() 。
。
差异在于复数指数相位因子中没有负号。
最后,让我们引入平移和缩放算子。有两种使用 σ 和 τ 的方法,具体取决于顺序; 是的,它们会得出相同的答案。一方面,
![]() ,
,
因为(注意括号和运算顺序!)
![]() 。
。
则
![]() 。
。
有效。
2.3.7 涉及Fourier变换的Parseval 恒等式(Parseval’s Identity)
我们之前顺便提到过Parseval恒等式。它指出
并且是Fourier级数的Rayleigh 恒等式Fourier变换的类比。这里,我们将推导更一般的表达式(也称为Parseval恒等式):
令 f = g 给出第一个版本。
继续下一步,
(应用逆Fourier变换到 g 和 ℱg ,这是关键 )
------------------------------------ (复数共轭)
(复数共轭)
-------------------------------------![]()
-------------------------------------![]() (更改积分顺序并交换双积分和迭代积分)
(更改积分顺序并交换双积分和迭代积分)
-------------------------------------![]() 。
。
完美!不用说,各个步骤都需要各种各样的数学假设。但我们不需要。至少现在还不行。
逆Fourier变换的 Parseval 恒等式与Fourier变换相同:
如果Parseval恒等式让你想起内积和范数,说明你的记忆力真不错!在实数域 ℝ 上两个函数的内积定义为
![]() ,
,
当积分有意义的时候,这个范数是
因此,Parseval恒等式通常写为
( f , g) = (ℱ f, ℱ g) ,
则也有
|| f || = || ℱ f || 。
后面,我们会一步讨论这个恒等式。
2.3.8 Fourier变换的导数定理(Derivative Theorems)
有人可能会说我把最好的属性留到了最后。有两个导数定理,每个定理都说明了Fourier叶变换将微分与乘法联系起来的重要且令人惊讶的属质:
![]() ,
,
ℱ f ’(s ) = 2πit ℱ f (s ) 。
对于第一个表达式,
![]()
----------------------------------![]()
----------------------------------![]()
----------------------------------![]()
----------------------------------![]() 。
。
关键的数学问题是将微分与积分互换。关键的符号问题是没有好的方法将变量 s 包含在右侧。对于这两个问题,你只需要知道自己在做什么。这就是挑战。
对于第二个等式,对 f (t )的差商进行Fourier变换:
----------------------------------------------![]() (使用平移定理)
(使用平移定理)
----------------------------------------------![]() 。
。
为了引入导数,我们需要对差商取极限。现在,
它是,
![]() 。
。
因此,
--------------------![]() 。
。
这次的数学问题是将 ![]() 与积分互换。这就是挑战。
与积分互换。这就是挑战。
我们可以重复应用每个公式来获得更Fourier变换高阶导数的版本:
![]() 。
。
逆Fourier变换的公式是什么?这只是改变符号(译注:![]() 和后面的-号)的问题:
和后面的-号)的问题:
![]() 。
。
2.4 Fourier变换的不定定义格式以及因此公式发生的变化(Different Definitions of the Fourier Transform, and What Happens to the Formulas)
我之前提到,不同的领域可能采用不同的Fourier变换及其变换的定义,也许更适合应用,或者可能反而更为困难。根据 T. W. Körner 在他的<
常见格式为
以下是常见于实践中的选择:
![]() -------------------B =±1 ,
-------------------B =±1 ,
A = 1 ------------------- B =±2π ,
A = 1 ------------------- B =±1 ,
我在本书中的定义选择的是 A = 1 ,B = -2π 。
对于一般的 ℱ,在 A 和 B未指定的情况下,我们有
![]() ,
,
![]() ,
,
![]() (保持不变),
(保持不变),
ℱ ( f ’ ) = -iBℱf ,
对于Parseval恒等式,我简单写出一些案例:
还有一个用于卷积的,我们将在下一章中遇到。为了方便起见,这里列出了结果:
ℱ ( f * g) = A(ℱf )( ℱg) 。
还要认识到,改变 ℱf 定义中的常数将会改变特定Fourier变换的公式。例如,
内容来源:
<
参考资料:
<
<< Fourier Analysis for Beginners>> Larry N. Thibos
<