【剑指offer】栈与队列4题 全刷(详解)
目录
目录
目录
[简单]剑指 Offer 09. 用两个栈实现队列
题目
方法
[简单]剑指 Offer 30. 包含min函数的栈
题目
方法1:笨办法
方法2:辅助栈
[困难]剑指 Offer 59 - I. 滑动窗口的最大值
题目
方法:单调队列
[中等]剑指 Offer 59 - II. 队列的最大值
题目
方法1:暴力for
方法2:辅助双端队列
心得
[简单]剑指 Offer 09. 用两个栈实现队列
题目
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
剑指 Offer 09. 用两个栈实现队列 - 力扣(LeetCode)
方法
思路
将一个栈当作输入栈,用于压入 appendTail 传入的数据;另一个栈当作输出栈,用于 deleteHead操作。
每次 deleteHead时,若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。
代码
class CQueue {
Stack stack1 ;
Stack stack2 ;
public CQueue() {
stack1 = new Stack<>();//入栈
stack2 = new Stack<>();//出栈
}
public void appendTail(int value) {
stack1.add(value);
}
public int deleteHead() {
//先看 出栈 空就 把入栈的数据全部倒入到出栈
if (stack2.isEmpty()){
if (!stack1.isEmpty()){
while (!stack1.isEmpty()){
stack2.add(stack1.pop());
}
}
}
if (!stack2.isEmpty()){
int res = stack2.pop();
return res;
}else return -1;
}
} 效果
[简单]剑指 Offer 30. 包含min函数的栈
题目
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例:
MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.min(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.min(); --> 返回 -2.
剑指 Offer 30. 包含min函数的栈 - 力扣(LeetCode)
方法1:笨办法
思路
求最小值?直接用迭代器遍历这个栈,找到最小值。
朴实无华
代码
class MinStack {
Stack stack ;
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<>();
}
public void push(int x) {
stack.push(x);
}
public void pop() {
stack.pop();
}
public int top() {
return stack.peek();
}
public int min() {
int min = stack.peek();
Iterator iterator = stack.iterator();
while (iterator.hasNext()) {
Integer next = (Integer) iterator.next();
if (min > next){
min = next;
}
}
return min;
}
}
效果
效果超级低,可见这个方法真的无脑、不好
我总是能第一时间想出最蠢的办法
方法2:辅助栈
思路
根据题意,我们需要在常量级的时间内找到最小值!
这说明,我们绝不能在需要最小值的时候,再做排序,查找等操作来获取!
所以,我们可以创建两个栈,一个栈是主栈,另一个是辅助栈 ,用于存放对应主栈不同时期的最小值。
代码
class MinStack {
Deque xStack;
Deque minStack;
public MinStack() {
xStack = new LinkedList();
minStack = new LinkedList();
minStack.push(Integer.MAX_VALUE);
}
public void push(int x) {
xStack.push(x);
minStack.push(Math.min(minStack.peek(), x));
}
public void pop() {
xStack.pop();
minStack.pop();
}
public int top() {
return xStack.peek();
}
public int min() {
return minStack.peek();
}
}
效果
[困难]剑指 Offer 59 - I. 滑动窗口的最大值
题目
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。
示例:
输入: nums =[1,3,-1,-3,5,3,6,7], 和 k = 3 输出:[3,3,5,5,6,7] 解释:滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
剑指 Offer 59 - I. 滑动窗口的最大值 - 力扣(LeetCode)
同下面的题
239. 滑动窗口最大值 - 力扣(LeetCode)
方法:单调队列
头疼欲裂,第一次看到困难题,直接暴力肯定能做,但是大概率也是超时,想了半天想不出,只能硬着头皮看题解、教学视频。
想到了要用队列,但是接下来就没思路了。
很喜欢评论区里的一段话,他用一个很贴切的例子来说明出了这道题的解法,可以品味一下。
“
虫子的世界
发布于 广东
(编辑过)
2021.11.08
单调队列真是一种让人感到五味杂陈的数据结构,它的维护过程更是如此.....就拿此题来说,队头最大,往队尾方向单调......有机会站在队头的老大永远心狠手辣,当它从队尾杀进去的时候,如果它发现这里面没一个够自己打的,它会毫无人性地屠城,把原先队里的人头全部丢出去,转身建立起自己的政权,野心勃勃地准备开创一个新的王朝.....这时候,它的人格竟发生了一百八十度大反转,它变成了一位胸怀宽广的慈父!它热情地请那些新来的“小个子”们入住自己的王国......然而,这些小个子似乎天性都是一样的——嫉妒心强,倘若见到比自己还小的居然更早入住王国,它们会心狠手辣地找一个夜晚把它们通通干掉,好让自己享受更大的“蛋糕”;当然,遇到比自己强大的,它们也没辙,乖乖夹起尾巴做人。像这样的暗杀事件每天都在上演,虽然王国里日益笼罩上白色恐怖,但是好在没有后来者强大到足以干翻国王,江山还算能稳住。直到有一天,闯进来了一位真正厉害的角色,就像当年打江山的国王一样,手段狠辣,野心膨胀,于是又是大屠城......历史总是轮回的。
”
当然了,如果你直接初读这段话也是不好理解的,建议在看几遍题解之后,再读这段话就懂了。
如果题解不好看懂,我推荐看这个视频
单调队列正式登场!| LeetCode:239. 滑动窗口最大值_哔哩哔哩_bilibili
搞不懂,以后遇到滑动窗口或者单调队列这样的再补一下这块吧。。。
[中等]剑指 Offer 59 - II. 队列的最大值
题目
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
示例 1:
输入: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"] [[],[1],[2],[],[],[]] 输出: [null,null,null,2,1,2]
示例 2:
输入: ["MaxQueue","pop_front","max_value"] [[],[],[]] 输出: [null,-1,-1]
限制:
1 <= push_back,pop_front,max_value的总操作数 <= 100001 <= value <= 10^5
剑指 Offer 59 - II. 队列的最大值 - 力扣(LeetCode)
方法1:暴力for
思路
队列我们用数组去模拟,两个指针,一个in,一个out,初始的时候都是指向-1,执行入队列的时候就in++,执行出队列的时候,就是out++,所以队列的有效范围就是arr[out] , arr[in] ,前开后闭。
求最大值的操作就是遍历一遍这个队列,返回最大值即可。
代码
class MaxQueue {
int arr[] = new int[10000];
int in = -1;
int out = -1;
public MaxQueue() {
}
public int max_value() {
if (!isNull()){
int max = Integer.MIN_VALUE;
for (int i = this.out+1; i <= this.in; i++) {
if (arr[i] > max){
max = arr[i];
}
}
return max;
}else return -1;
}
public void push_back(int value) {
in ++;
arr[in] = value;
}
/**
* 为空
*/
public boolean isNull(){
if (this.out >= this.in){
return true;
}else return false;
}
public int pop_front() {
if (!isNull()){
out ++;
return arr[out];
}else return -1;
}
}
方法2:辅助双端队列
思路
思路和图解取自
作者:腐烂的橘子
链接:https://leetcode.cn/problems/dui-lie-de-zui-da-zhi-lcof/solutions/136701/ru-he-jie-jue-o1-fu-za-du-de-api-she-ji-ti-by-z1m/
我们知道对于一个普通队列,push_back 和 pop_front 的时间复杂度都是 O(1),因此我们直接使用队列的相关操作就可以实现这两个函数。
对于 max_value 函数,我们通常会这样思考,即每次入队操作时都更新最大值:
但是当出队时,这个方法会造成信息丢失,即当最大值出队后,我们无法知道队列里的下一个最大值。
为了解决上述问题,我们只需记住当前最大值出队后,队列里的下一个最大值即可。
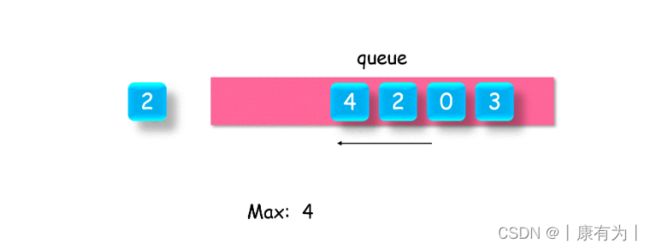
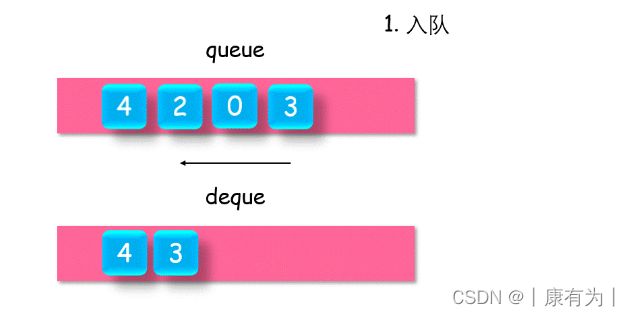
具体方法是使用一个双端队列 deque,用于记录最大值,在每次入队时,如果 deque 队尾元素小于即将入队的元素 value,则将小于 value 的元素全部出队后,再将 value 入队;否则直接入队。
当3进入时,3比辅助队列中的0 和 2 大,所以3进入了后辅助队列中的2 0 就没用了,将2 0 移出辅助队列,因为是双端队列,所以2 0 可以从队尾走出去。
出队列就简单了,出之前判断一下连队列的头和辅助队列的头是不是同一个,是同一个就一起出,不是的话就只出队列的头,不出辅助队列的头。
代码
class MaxQueue {
//用链表来模拟队列
LinkedList list;
//辅助队列,用链表来模拟双端队列
LinkedList helpList;
public MaxQueue() {
list = new LinkedList<>();
helpList = new LinkedList<>();
}
public int max_value() {
if(helpList.isEmpty())return -1;
return helpList.peekFirst();
}
//入队列
public void push_back(int value) {
list.add(value);
//如果新来的value 比 辅助队列前面的值大,那么前面的值都没有用了,将前面的比value小的值都从末尾排出
while(!helpList.isEmpty() && helpList.peekLast() < value){
helpList.pollLast();
}
//再将新来的大一大一点的这个value 入到辅助队列中
helpList.offer(value);
}
//出队列
public int pop_front() {
if(list.isEmpty()) return -1;
//如果队列的头 和 辅助队列的头 一样,那就两个队列都一起出
if(list.peekFirst().equals(helpList.peekFirst())){
helpList.pollFirst();
return list.pollFirst();
}
//否则只出队列的
return list.pollFirst();
}
} 效果
(效果不好的话,多提交几次)
心得
1. 如果一道题实在想不出来好的方法,那能用for就用for吧,说不定暴力的解法也能过。
2. 多熟悉API,java的这个LinkedList太好用了,既可用于队列,又能模拟双端队列,实用性非常强,因为它可以查看、删除对头队尾的元素,所以灵活性很高,可以多用用这个。