智能优化算法:人类行为优化算法-附代码
智能优化算法:人类行为优化算法
文章目录
- 智能优化算法:人类行为优化算法
-
- 1.人类行为优化
- 2.实验结果
- 3.参考文献
- 4.Matlab
- 5.python
摘要:HBBO 是 Seyed-Alireza Ahmadi 于 2017 年基于人类行为而提出的一种新型元启发式优化算法。。具有寻优能力强,收敛速度快等特点。
1.人类行为优化
该算法基于以下假设: (1)所有初始个体都分布在不同领 域; (2)各领域中, 每个个体都试图通过教育来提高 自己; (3)每个个体从全社会中随机寻找顾问进行咨 询; (4)在某些领域, 个体可能会改变他的学习领域 。 HBBO 算法描述简述如下:
(1)初始化。在具有 N v a r N_{\mathrm{var}} Nvar 个变量的优化问题中, 通过式(2)随机生成 N pop N_{\text {pop }} Npop 个初始个体, 并将其随机分 配到不同领域, 这些个体构成社会, 每个领域初始 个体数量通过式 (3) 表示; 初始个体函数值计算公式为
Individual = [ x 1 , x 2 , ⋯ , x N v m ] ( 2 ) N . Ind i = round { N p o p / N field } ( 3 ) function valua = f ( x 1 , x 2 , ⋯ , x N v e r ) ( 4 ) \begin{aligned} \text { Individual } & =\left[x_1, x_2, \cdots, x_{N_{\mathrm{vm}}}\right](2) \\ N . \operatorname{Ind}_i & =\operatorname{round}\left\{N_{\mathrm{pop}} / N_{\text {field }}\right\} (3)\\ \text { function valua } & =f\left(x_1, x_2, \cdots, x_{N_{\mathrm{ver}}}\right)(4) \end{aligned} Individual N.Indi function valua =[x1,x2,⋯,xNvm](2)=round{Npop/Nfield }(3)=f(x1,x2,⋯,xNver)(4)
式中, Individual 为初始个体; N v a r N_{\mathrm{var}} Nvar 为变量数量; N . I n d i N . \mathrm{Ind}_i N.Indi 为第 i i i 个领域个体数量; N pop N_{\text {pop }} Npop 为个体总量; N field N_{\text {field }} Nfield 为领域数量; function valua 为函数值。
(2) 教育。 H B B O \mathrm{HBBO} HBBO 算法中, 每个个体都试图通过 向自己领域中最优个体(专家个体) 进行学习来提高 自己 (专家个体为各领域中具有最佳适应度值的个 体)。
(3)咨询。 HBBO 算法中, 每个个体(最优个体 除外)从全社会中随机寻找顾问并咨询。在咨询过程 中, 如果新变量具有更好的函数值, 则将原变量替 换为新变量; 否则保留原变量。将被改变的随机变 量数量表示为
N c = round { σ × N v a r } (5) N_c=\operatorname{round}\left\{\sigma \times N_{\mathrm{var}}\right\} \tag{5} Nc=round{σ×Nvar}(5)
式中, σ \sigma σ 为咨询因子; 其他参数意义同上。
(4)领域变化概率。在迭代过程中, 某些领域 个体可能会改变他的学习领域。HBBO 算法采用秩 概率法计算每个领域的变化概率, 每个领域根据其 各自的函数值进行排序。即
sort fields = [ field 1 , field 2 , ⋯ , field n ] (6) \text { sort fields }=\left[\text { field }_1, \text { field }_2, \cdots, \text { field }_n\right] \tag{6} sort fields =[ field 1, field 2,⋯, field n](6)
式中, sort fields 为领域排序; field 、 、 、 field n n n 分别为具 有最差和最佳适应度值的专家个体。每个领域的变 化概率计算公式为
P i = O i / ( N field + 1 ) (7) P_i=O_i /\left(N_{\text {field }}+1\right) \tag{7} Pi=Oi/(Nfield +1)(7)
式中, P i 、 O i P_i 、 O_i Pi、Oi 分别为第 i i i 个领域变化概率和排序 顺序。
通过上述计算, 具有更好适应度值的专家个体 其领域变化可能性较小, 而具有较差适应度值的专 家个体其领域变化可能性较大。在领域变化过程中, 根据函数值, 定义每个个体的选择概率为
P . S j = ∣ f ( Individual j ) / ∑ k = r N i = 1 f ( Individual k ) (8) P . S_j=\mid f\left(\text { Individual }_j\right) / \sum_{k=\mathrm{r}}^{N_{i=1}} f\left(\text { Individual }_k\right) \tag{8} P.Sj=∣f( Individual j)/k=r∑Ni=1f( Individual k)(8)
式中, P . S j P . S_j P.Sj 为第 j j j 个个体的选择概率; N ind N_{\text {ind }} Nind 为所选领 为第 k k k 个个体, k = 1 , 2 , ⋯ , N ind k=1,2, \cdots, N_{\text {ind }} k=1,2,⋯,Nind 。
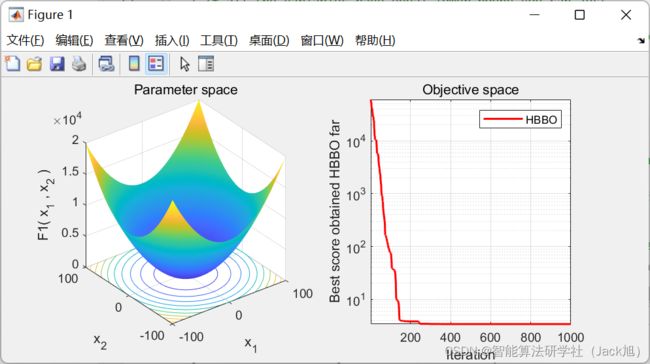
2.实验结果
3.参考文献
[1] Ahmadi, Seyed-Alireza. “Human Behavior-Based Optimization: a Novel Metaheuristic Approach to Solve Complex Optimization Problems.” Neural Computing and Applications, vol. 28, no. S1, Springer Science and Business Media LLC, May 2016, pp. 233–44, doi:10.1007/s00521-016-2334-4.