Practices9(双指针)|283. 移动零、11. 盛最多水的容器、15. 三数之和
283. 移动零
1.题目:
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums =[0,1,0,3,12]输出:[1,3,12,0,0]
示例 2:
输入: nums =[0]输出:[0]
2.思路:
双指针左指针的左面全是不为零的数,右指针去寻找,找到不为零的和左指针交换,做指针加加,右指针继续寻找,直到找到数组长度的尾巴。
-
左指针左边均为非零数;
-
右指针左边直到左指针处均为零
因此每次交换,都是将左指针的零与右指针的非零数交换,且非零数的相对顺序并未改变
3.代码:
class Solution {
public void moveZeroes(int[] nums) {
int left=0,right=0;
while(right11. 盛最多水的容器
1.题目:
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
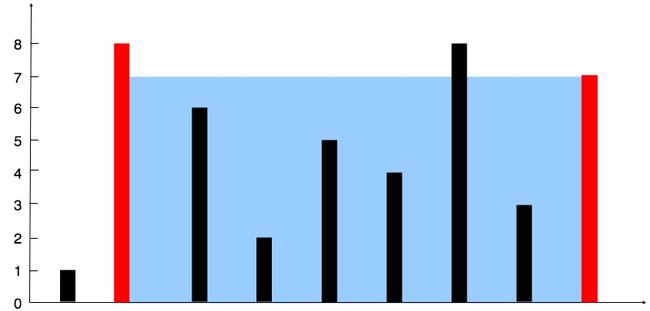
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
2.思路:
双指针遍历,但是数据多,优化两个指针一前一后的去遍历。
若向内 移动短板 ,水槽的短板 可能变大,因此下个水槽的面积 可能增大 。
若向内 移动长板 ,水槽的短板不变或变小,因此下个水槽的面积 一定变小
3.代码:
class Solution {
public int maxArea(int[] height) {
int cap=0;
/*for(int i=0;i15. 三数之和
1.题目:
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
2.思路:
先遍历一个数,求和问题就变成了两数求和。
注意去重问题!!对每个元素去重。当下一个遍历的元素和当前元素相同时,考虑去重问题。
3.代码:
lass Solution {
public List> threeSum(int[] nums) {
List> res=new ArrayList<>();
Arrays.sort(nums);
for(int i=0;i0){
return res;
}
if(i>0 && nums[i]==nums[i-1]){
continue;
}
int left=i+1,right=nums.length-1;
while(lefttemp){
right--;
}else{//找到了
res.add(Arrays.asList(nums[i],nums[left],nums[right]));
while(left< right && nums[left]==nums[left+1]){
left++;
}
while(left