《算法竞赛·快冲300题》每日一题:“造电梯”
《算法竞赛·快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。
文章目录
- 题目描述
- 题解
- C++代码
- Java代码
- Python代码
“ 造电梯” ,链接: http://oj.ecustacm.cn/problem.php?id=1790
题目描述
【题目描述】 现在给你一张建筑的平面图,按照要求,建筑的每一个部分都应该是轮椅使用者可以到达的,这意味着必须安装电梯。
给定的平面图是一个n*m的矩阵,里面的数字表示这个位置的高度。可以在建筑中的任意位置放置电梯,电梯可以停在所有楼层。
需要保证可以使用电梯到达所有高楼层。相同高度的楼层之间是互通的,联通准则是四联通。
需要求解最少需要多少个电梯,注意高度为1的不需要电梯。
下图展示了样例2的可视化三维图。
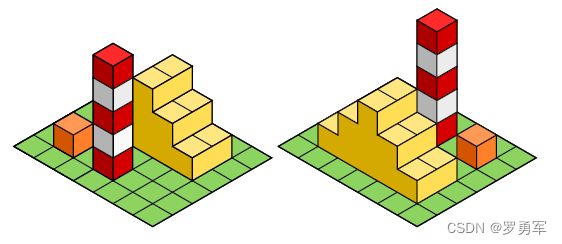
【输入格式】 输入第一行为n和m(1≤n,m≤500)。
接下来n行,每行m个整数xij,表示平面图,0≤xij≤10^9。
【输出格式】 输出最少电梯数量
【输入样例】
样例1:
2 3
1 2 3
1 3 2
样例2:
6 7
0 0 0 0 0 0 0
0 1 2 3 2 1 0
0 1 2 3 2 1 0
0 0 0 0 0 0 0
0 1 0 5 0 0 0
0 0 0 0 0 0 0
【输出样例】
样例1:
2
样例2:
2
题解
电梯是装在建筑内部的,例如样例2,高度5的柱子内部需要一个电梯,楼梯状的建筑也需要一个电梯。
注意一个建筑内部可能需要不止一个电梯,例如平面上一个建筑的高度是{5, 2, 4},那么需要在5和4上建2个电梯。
本题是“洪水填充(《算法竞赛》清华大学出版社,罗勇军,郭卫斌著,120页,3.3 洪水填充)”的应用:从最高处开始倒水,那么水会平流或者往下流,这相当于建了一部电梯;这次倒水没有流到的地方,继续从下一个最高处倒水…
以样例2为例:
(1)从最高的“5”开始倒水,水会平流或往下流,那么会继续淹没所有的“0”。这次倒水相当于建设了一部电梯。没有被这次倒水淹没的有第二行和第三行的“1 2 3 2 1”,还有倒数第二行的“1”。
(2)继续从剩下的最高点“3”开始倒水,水会平流或往下流,那么第二行和第三行的“1 2 3 2 1”,还有所有的“0”都会淹没。这次倒水也相当于建设了一部电梯。没有被这次倒水淹没的有倒数第二行的“1”,不过它不需要建设电梯。
“洪水填充”用BFS或DFS都行,下面的代码用BFS实现。把平面的所有点放进优先队列,然后依次取出队列中的最高点,并从它开始“洪水填充”。
【重点】 洪水填充。
C++代码
代码的计算复杂度,设平面上共n个点,每个点只需要处理一次,优先队列进出一次是O(logn)的,所以总复杂度O(nlogn)。
#include Java代码
import java.util.*;
class Point implements Comparable<Point> {
int x, y, h;
public Point(int x_, int y_, int h_) {
x = x_;
y = y_;
h = h_;
}
public int compareTo(Point r) { return Integer.compare(-h, -r.h); }
}
public class Main {
static int[] dx = { 1, 0, -1, 0 };
static int[] dy = { 0, 1, 0, -1 };
static int n, m;
static int[][] a;
static boolean[][] done;
public static void floodfill(int x, int y) {
done[x][y] = true;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx < 0 || nx >= m || ny < 0 || ny >= n || done[nx][ny])
continue;
if (a[nx][ny] <= a[x][y])
floodfill(nx, ny);
}
}
public static void floodfill_bfs(int sx, int sy) {
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[] { sx, sy });
done[sx][sy] = true;
while (!queue.isEmpty()) {
int[] curr = queue.poll();
int x = curr[0];
int y = curr[1];
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !done[nx][ny] && a[nx][ny] <= a[x][y]) {
queue.add(new int[] { nx, ny });
done[nx][ny] = true;
}
}
}
}
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
n = input.nextInt();
m = input.nextInt();
a = new int[m][n];
done = new boolean[m][n];
PriorityQueue<Point> Q = new PriorityQueue<>();
for (int j = 0; j < n; j++) {
for (int i = 0; i < m; i++) {
a[i][j] = input.nextInt();
done[i][j] = (a[i][j] <= 1);
if (a[i][j] > 1) Q.add(new Point(i, j, a[i][j]));
}
}
int ans = 0;
while (!Q.isEmpty()) {
Point p = Q.poll();
if (!done[p.x][p.y]) {
ans++;
floodfill_bfs(p.x, p.y);
}
}
System.out.println(ans);
input.close();
}
}
Python代码
from collections import deque
import heapq
import sys
input = sys.stdin.readline
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]
n, m = map(int, input().split())
a = [[0] * n for _ in range(m)]
done = [[False] * n for _ in range(m)]
Q = []
for j in range(n):
row_a = list(map(int, input().split()))
for i in range(m):
a[i][j] = row_a[i]
if a[i][j] <= 1: done[i][j]=True
else: heapq.heappush(Q, (-a[i][j], i, j))
ans = 0
while Q:
_, sx, sy = heapq.heappop(Q)
if not done[sx][sy]:
ans += 1
q = deque([(sx, sy)])
done[sx][sy] = True
while q:
x, y = q.popleft()
for i in range(4):
nx, ny = x + dx[i], y + dy[i]
if 0 <= nx < m and 0 <= ny < n and not done[nx][ny] and a[nx][ny] <= a[x][y]:
q.append((nx, ny))
done[nx][ny] = True
print(ans)