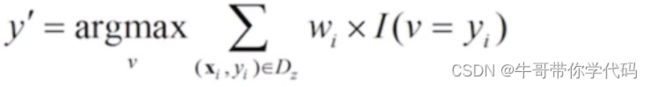KNN分类器、神经网络原理基础与代码实现
急切学习
两步：（1）归纳 （2）演绎
例如：贝叶斯分类器、决策树分类等等。
惰性学习
将训练数据建模过程推迟到需要对样本分类时（直观理解：死记硬背，记住所有的训练数据，仅仅当记录的属性值与一个训练记录完全匹配才与它分类）
实例：knn分类器
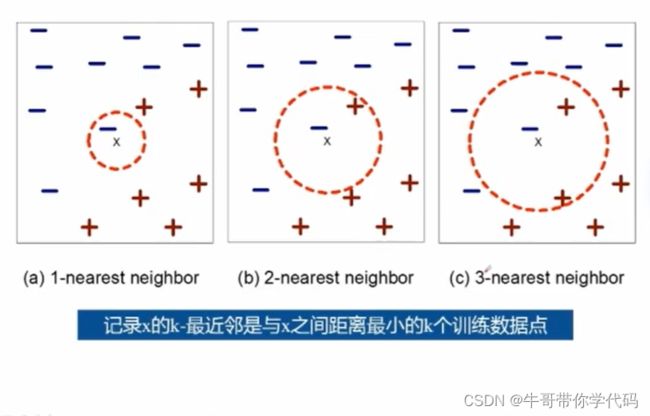
最近邻
使用“最近”的k个点（最近邻）进行分类
k-最近邻分类算法
1、令k是最近邻数目，D是训练样例的集合
2、for每个测试样例z=(x',y') do
3、计算z和每个样例（x，y）∈D之间的距离d(x',x) (此处的计算开销很大)
4、选择离z最近的k个训练样例的集合Dz
5、 
v
6、end for
距离加权表决
两种特殊的数据结构提前对训练集进行优化存储
- Kd-Tree
- Kd-Ball
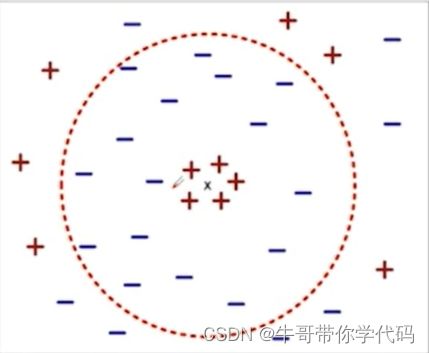
k值的选择
1、如果k太小，则对噪声点敏感
2、如果k太大，邻域可能包含很多其他类的点
规范化
属性可能需要规范化，防止距离度量被具有很大值域的属性所左右。
代码实现
支持向量机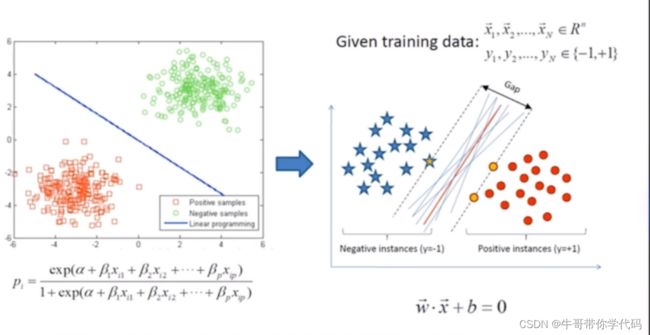
线性不可分的解决方案：核变化将低维空间数据映射到高维空间。
感知机
最简单的神经网络的雏形：感知机
感知机通过有限次训练就能学会正确的行为。属于线性可分的分类器。
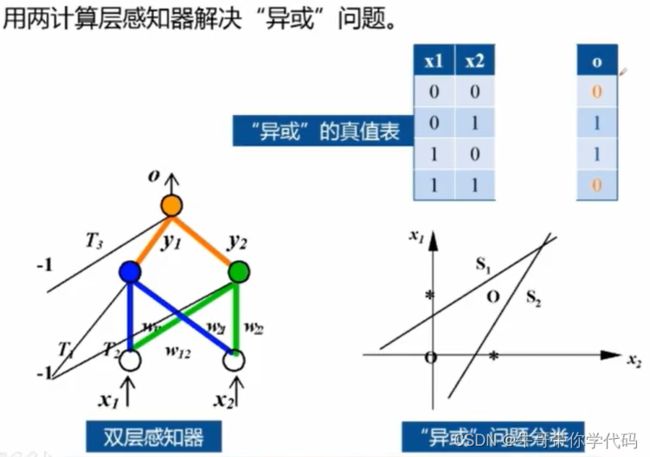
感知机没法解决异或这种线性不可分问题。所以为了解决线性不可分问题，我们将多个线性分类器进行组合，然后得到了多层感知机。对多层感知机进行进一步的延伸就获得了多层神经网络。
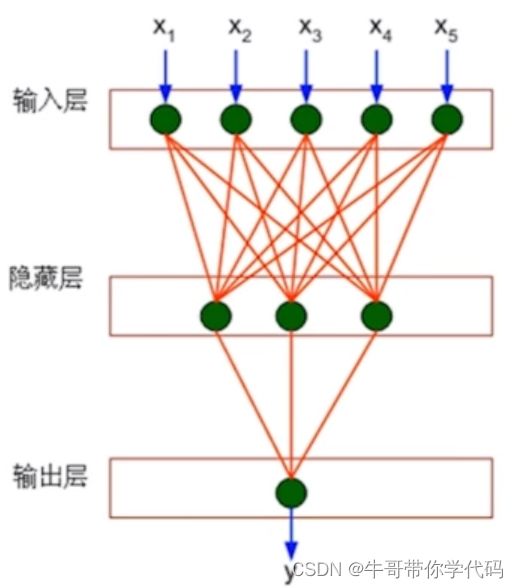
神经网络
神经网络模型比感知机模型更为复杂，输入层与输出层之间包含隐藏层
最经典： 误差反向传播（BP）神经网络
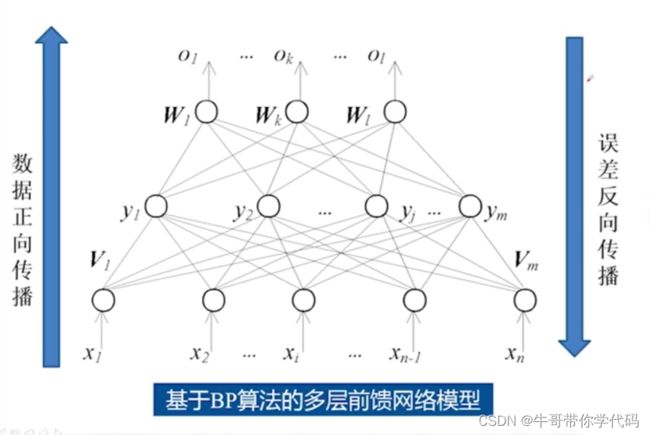
从下往上会存在一个输入，由权值我们可以正向地获得一个输出值，这个输出又称作预测值， 误差会从上向下进行反向传播，总而言之，存在数据正向传播，误差反向传播。
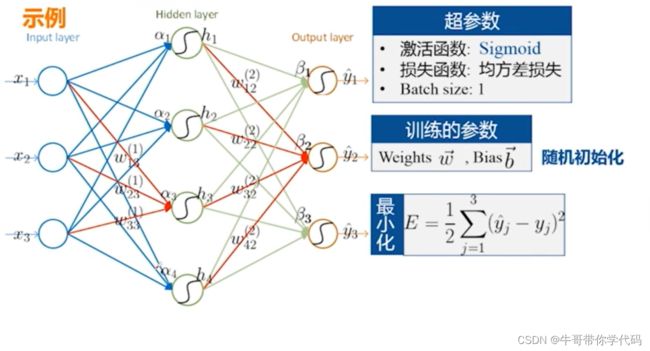
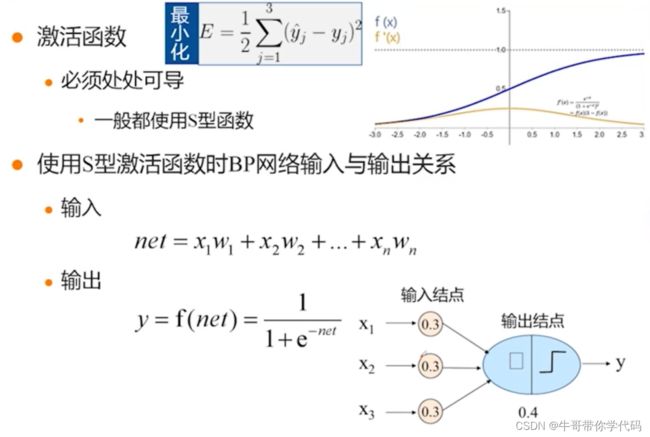
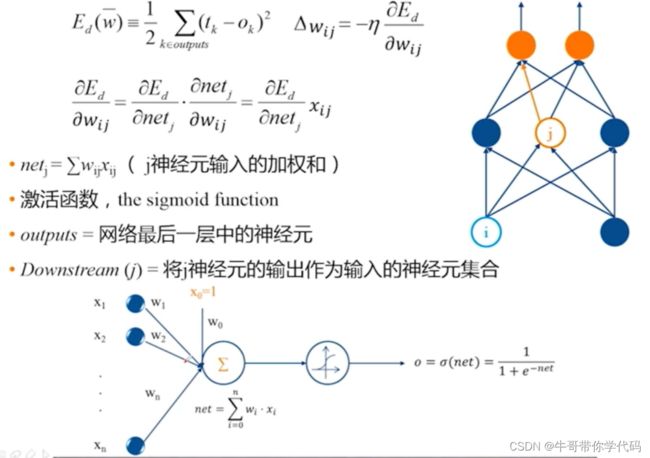
通常在BP神经网络中我们选择的激活函数为Sigmoid函数，其中Sigmoid函数的特点为处处可导。输入为加权求和的值。对于加权求和得到的数值，代入Sigmoid函数进行进一步的计算，假如这个数值大于0.5，那么该数值属于正类，假如小于0.5，则认为他属于负类。
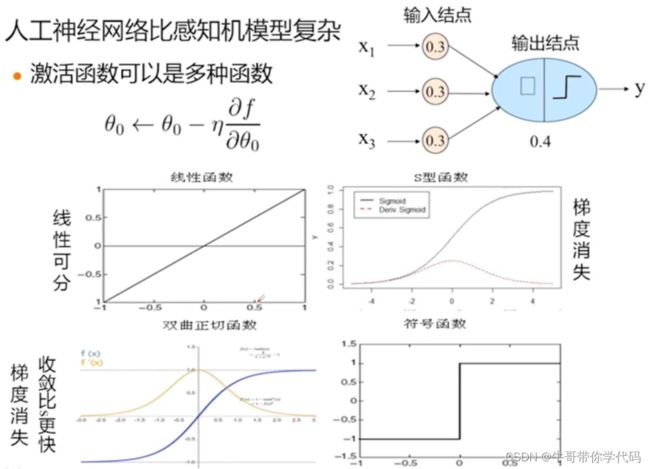
线性函数的梯度为0，那么在权值调整过程中没法使用上述减去学习率减去偏导数的方式调整权值，因此在线性函数中较少使用上述方法进行调整。
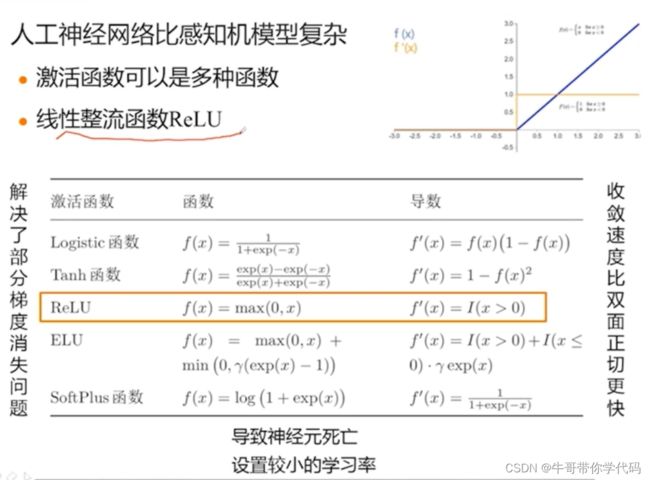
对于Sigmoid函数和双面正切函数均存在梯度消失问题，对此，我们为了解决激活函数中的梯度消失问题，我们还常会使用线性整流函数作为梯度函数。
假如大于0，那么就会是一个直线，权值每次都可以通过这个常数进行调整，但是，假如输入是负值的话，偏导会是0，就会出现和前面的线性可分一样，没办法对权值进行下一步的调整。也就导致了神经元的死亡。所以当使用线性整流函数时，我们通常要设置一个较小的学习率。
BP神经网络的主要流程
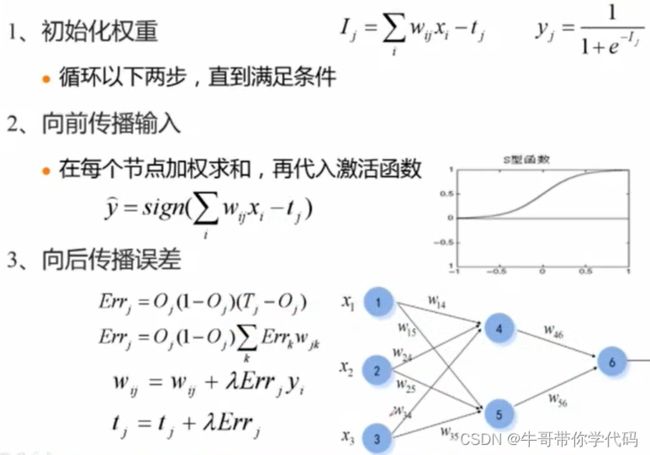
BP神经网络的求解过程
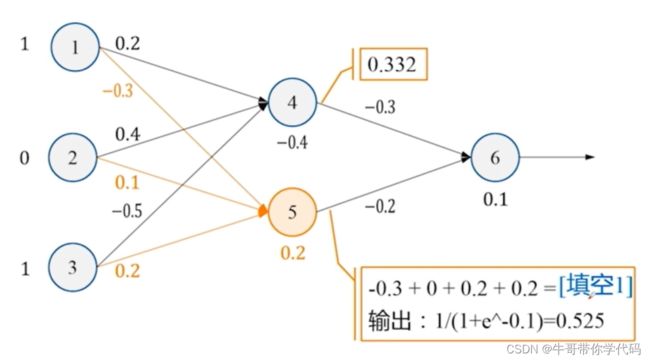
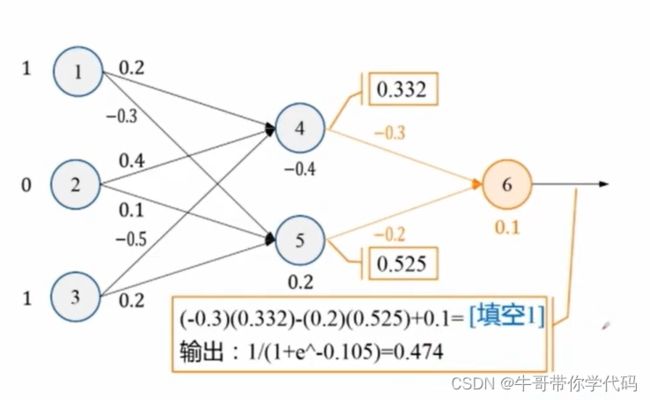
首先使用各个神经元的数值与对应的权值相乘再相加，将数值加上偏置项，最终将对应的数值代入激活函数Sigmoid即可获得输出。 再将获得的第二层神经网络的数值作为第三层神经元的输入进行下一步计算，即可获得最后的结果。
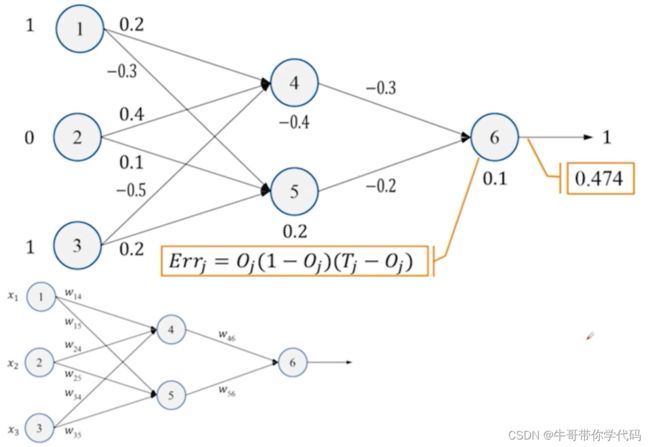
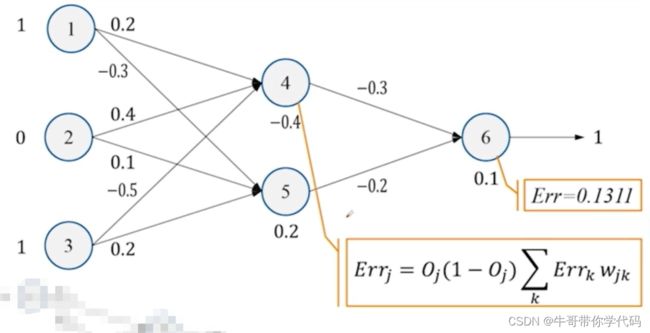
误差计算
预测输出Oj
真实输出Tj
Errj=Oj(1-Oj)(Tj-Oj)
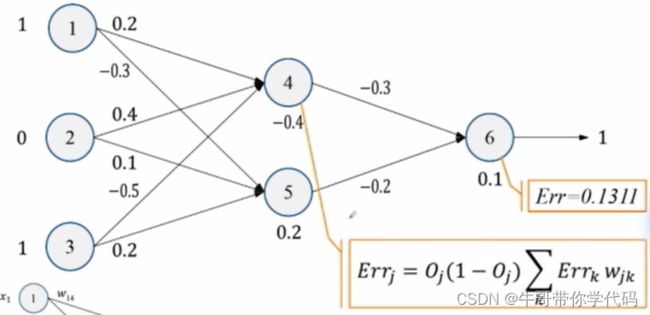
得到对应的误差后，再对误差进行下一步的反向传播。求解反向传播误差的公式
求解第四个神经元的误差
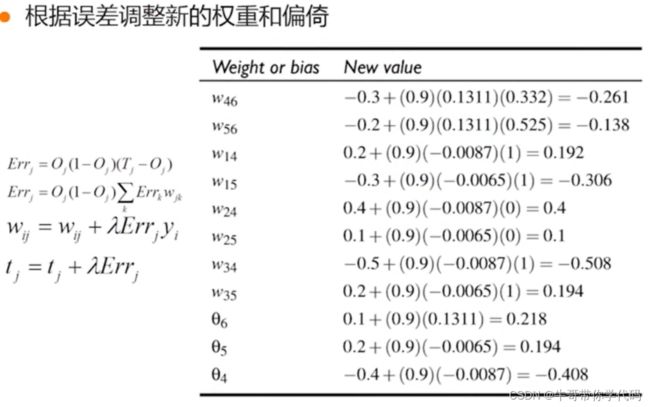
下一步对权值进行下一步的调整，根据梯度下降法的原理可知
权值调整公式=初始权值+学习率*对应误差*对应y
对于学习率取值大小对迭代过程的影响：
假如学习率过大的话，可能能够很快地跳到收敛点， 但是不一定能够到达最优的收敛点，可能会在收敛点来回进行一个徘徊。没法达到最优的解；假如学习率太小的话，可能到达收敛点的步子很小，到达收敛点的次数要很多次才能够到达。
后向传播算法的推导
后向传播BP网络注意事项
初始值选择
权值向量以及阀值的初始值应设定在一均匀分布的小范围内
初始值不能为零，否则性能曲面会趋向于鞍点
为什么鞍点不好，因为他在一个维度上面是最小值，而在另外一个维度上面又是最大值，不符合我们想要找的在所有维度都是最小值的情况。
初始值不能太大，否则远离优化点，导致性能曲面平坦，学习率很慢
训练样本输入次序
不同，也会造成不一样的学习结果
在每一次的学习循环中，输入向量输入网络的次序应使其不同
BP算法的学习过程的终止条件
权值向量的梯度<给定值
均方误差值<给定误差容限值
若其推广能力达到目标则予终止
可以结合上述各种方式
神经网络的主要特性：
1、普适性较强，精度较高
2、噪声敏感
3、训练非常耗时，但对目标分类较快
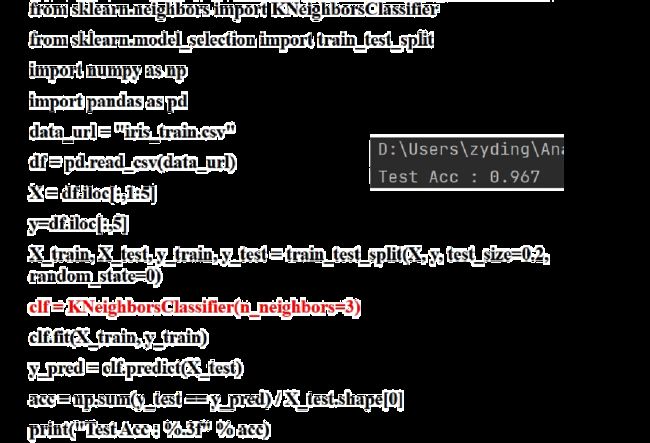
代码实现（多层感知机——MLP）
