DEBERTA: DECODING-ENHANCED BERT WITH DISENTANGLED ATTENTION

Paper: https%3A//arxiv.org/pdf/2006.03654.pdf
Code: https%3A//github.com/microsoft/DeBERTa
- 在DeBerta中单词间的权重分别根据其内容和相对位置使用解耦的矩阵进行计算。
- DeBERTa将上下文的内容和位置信息用于MLM。考虑这些词的绝对位置。
- 新的虚拟对抗训练方法,用于将PLM微调到下游NLP任务。
DEBERTA:具有分离注意力的解码增强型 BERT
预训练神经模型的研究已经显著提高了许多自然语言处理(NLP)任务的性能。本文提出了一种新的基于解耦注意的decoding增强BERT模型(DeBERTa),利用两种新技术对BERT模型和RoBERTa模型进行了改进。第一种是解耦注意机制,其中每个单词用两个向量表示,分别对其内容和位置进行编码,单词之间的注意权重使用内容和相对位置的解耦矩阵计算。其次,在模型预训练中,利用增强掩码解码器在解码层中加入绝对位置来预测掩码令牌;其次,在模型预训练中,利用增强掩码解码器在解码层中加入绝对位置来预测掩码token;此外,还采用了一种新的虚拟对抗训练方法进行微调,以提高模型的泛化能力。研究表明,这些技术显著提高了模型预训练的效率,以及自然语言理解(NLU)和自然语言生成(NLG)下游任务的性能。与RoBERTa-Large相比,在一半的训练数据上训练的DeBERTa模型在广泛的NLP任务上表现始终更好,在MNLI上提高了0.9%(90.2%比91.1%),在SQuAD v2.0上提高了2.3%(88.4%比90.7%),在RACE上提高了3.6%(83.2%比86.8%)。这种显著的性能提升使得单一DeBERTa模型在宏观平均分数(89.9对89.8)方面首次超过了人类在SuperGLUE基准上的表现(Wang ,2019a),而整体DeBERTa模型在2021年1月6日的SuperGLUE排行榜上位居榜首。远远超过人类基准(90.3对89.8)。
INTRODUCTION
Transformer已成为用于神经语言模型的最有效的神经网络体系结构。与按顺序处理文本的循环神经网络(RNN)不同,transformer应用self-attention功能来并行计算输入文本中的每个单词的注意力权重,从而衡量每个单词对另一个单词的影响,因此与RNN相比,它可以并行大规模模型训练(Vaswani et al.,2017)。自2018年以来,我们已经看到了一系列基于transformer的大规模预训练语言模型(PLM)的兴起,例如GPT(Radford等人,2019; Brown等人,2020),BERT(Devlin等人)。等人,2019),RoBERTa(Liu等人,2019c),XLNet(Yang等人,2019),UniLM(Dong等人,2019),ELECTRA(Clark等人,2020),T5(Raffel等人)等人,2020),ALUM(Liu等人,2020),StructBERT(Wang等人,2019c)和ERINE(Sun等人,2019)。这些PLM使用特定任务label进行了微调,并在许多下游自然语言处理(NLP)任务中创造了新的技术水平(Liu等人,2019b; Minaee等人,2020; Jiang等人,2020 ; He等人,2019a; b; Shen等人,2020)。
在本文中,我们提出了一种新的基于Transformer的神经语言模型DeBERTa(具有解耦注意力的解码增强BERT),它使用两种新颖的技术改进了以前的最新PLM:解耦注意力机制和增强的mask解码器。
解耦注意力: 与BERT不同,在BERT中,输入层中的每个单词都使用一个向量来表示,该向量是其单词(内容)嵌入和位置嵌入的总和, 在DeBerta中单词间的权重分别根据其内容和相对位置使用解耦的矩阵进行计算。 这是由于观察到一个单词对的注意力权重不仅取决于它们的内容,而且还取决于它们的相对位置。 例如,单词“deep”和“learning”相邻时的的关系要强于出现在不同句子中。
增强的mask解码器: 与BERT一样,DeBERTa也使用mask语言模型(MLM)进行了预训练。 MLM是一项填空任务,在该任务中,模型被教导要使用mask token周围的单词来预测mask的单词应该是什么。 DeBERTa将上下文的内容和位置信息用于MLM。解耦注意力机制已经考虑了上下文词的内容和相对位置,但没有考虑这些词的绝对位置,这在很多情况下对于预测至关重要。考虑一下句子“a new store opened beside the new mall”,其斜体字“store”和“mall”被mask以进行预测。尽管两个单词的局部上下文相似,但是它们在句子中扮演的句法作用不同。 (这里,句子的主题是“store”而不是“mall”。)这些句法上的细微差别在很大程度上取决于单词在句子中的绝对位置,因此考虑单词在语言模型中的绝对位置是很重要的。 DeBERTa在softmax层之前合并了绝对单词位置嵌入,在该模型中,模型根据词内容和位置的聚合上下文嵌入对Masked单词进行解码。
此外,我们提出了一种新的虚拟对抗训练方法,用于将PLM微调到下游NLP任务。 该方法可有效改善模型的泛化性能。
我们通过全面的实证研究表明,这些技术大大提高了预训练的效率和下游任务的性能。在NLU任务中,与RoBERTa-Large相比,在一半的训练数据上训练的DeBERTa模型在各种NLP任务中始终表现更好,对MNLI的改进为+ 0.9%(90.2%对91.1%)。 SQuAD v2.0改进为+2.3%(88.4%对90.7%),RACE增长了+ 3.6%(83.2%对86.8%)。在NLG任务中,DeBERTa在Wikitext-103数据集上的困惑度从21.6降低到19.5。我们通过预训练由48个包含15亿个参数的Transformer层组成的更大模型来进一步扩展DeBERTa。单个15亿参数的DeBERTa模型在SuperGLUE基准上(Wang,2019a)大大优于110亿个参数的T5(0.6%(89.3%对89.9%)),并首次超过了人类基线(89.9对89.8)。截至2021年1月6日,集成的DeBERTa模型位于SuperGLUE排行榜的顶部,比人类的基线要高出很多(90.3对89.8)。
BACKGROUND
TRANSFORMER
基于transformer的语言模型由堆叠的transformer块组成(Vaswani,2017)。每个块都包含一个多头self-attention层,后面是一个全连接的位置前馈网络。标准的self-attention机制缺乏编码单词位置信息的自然方法。因此,现有的方法给每个输入词的嵌入增加了位置偏差,使得每个输入词由一个向量表示,其值取决于其内容和位置。位置偏差可以使用绝对位置嵌入(Vaswani,2017; Radford,2019; Devlin,2019)或相对位置嵌入(Huang,2018; Yang,2019)来实现。研究表明,相对位置表示对于自然语言理解和生成任务更有效(Dai,2019; Shaw,2018)。提出的解耦注意力机制与所有现有方法的不同之处在于,我们表示每个输入词,通过使用两个对词的内容和位置进行编码的单独向量,并使用解耦的矩阵分别计算其内容和相对位置来计算词间的注意力权重。
MASKED LANGUAGE MODEL
基于transformer的PLM通常在大量文本上进行预训练,称为mask语言模型(MLM)模型,使用自监督目标来学习上下文单词表示(Devlin 2019)。具体来说,给定序列 X = { x i } X=\{x_i\} X={xi},我们通过随机masking其15%的token将其分解为 X ~ \widetilde{X} X ,然后训练由 θ θ θ参数化的语言模型,通过预测以 X ~ \widetilde{X} X 为条件的被masking的token x ~ \widetilde{x} x 来重构 X X X

其中 C C C是序列中被mask token的索引集。BERT的作者提议保持10%的mask token不变,另外10%的token由随机选择的token代替,其余的token由[MASK] token代替。
THE DEBERTA ARCHITECTURE
注意力解耦:内容和位置嵌入向量方法
对于序列中位置i处的token,我们使用两个向量, { H i } \{H_i\} {Hi}和 { P i ∣ j } \{P_{i|j}\} {Pi∣j}表示它,它们分别表示内容和与位置 j j j处的token的相对位置。 token i i i和 j j j之间的交叉注意力得分的计算可以分解为四个部分:

也就是说,一个单词对的注意力权重可以使用其内容和位置的解耦的矩阵计算为四个注意力(内容到内容,内容到位置,位置到内容和位置到位置)的得分的总和。
现有的相对位置编码方法在计算注意力权重时使用单独的嵌入矩阵来计算相对位置偏差(Shaw,2018; Huang,2018)。 这等效于仅使用等式2中的**“内容到内容”和“内容到位置”**来计算注意力权重。我们认为位置到内容也很重要,因为单词对的注意力权重不仅取决于它们的内容。根据它们的相对位置,只能使用内容到位置和位置到内容进行完全建模。 由于我们使用相对位置嵌入,因此位置到位置项不会提供太多附加信息,因此在我们的实现中将其从等式2中删除。
以单头注意力为例,标准的self-attention操作(Vaswani,2017)可以表述为:

其中, H ∈ R N x d H \in R^{Nxd} H∈RNxd代表输入隐藏向量, H o ∈ R N x d H_o \in R^{Nxd} Ho∈RNxd表示self-attention输出, W q , W k , W v ∈ R d x d W_q, W_k, W_v\in R^{dxd} Wq,Wk,Wv∈Rdxd为投影矩阵, A ∈ R N x N A \in R^{NxN} A∈RNxN为注意力矩阵, N N N为输入序列的长度, d d d为隐藏层的维度。
将 k k k表示为最大相对距离,将将 δ ( i , j ) ∈ [ 0 , 2 k ) \delta(i,j) \in [0,2k) δ(i,j)∈[0,2k)表示为从token i i i到token j j j的相对距离,定义为:
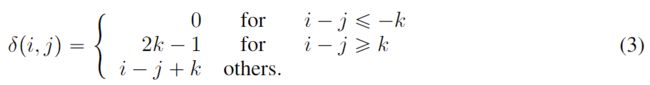
我们可以用等式4表示具有相对位置偏差的解耦的self-attention,其中 Q c Q_c Qc, K c K_c Kc和 V c V_c Vc是分别使用投影矩阵 W q , c , W k , c , W v , c ∈ R d x d W_{q,c},W_{k,c},W_{v,c} \in R^{dxd} Wq,c,Wk,c,Wv,c∈Rdxd生成的投影内容向量, P ∈ R 2 k x d P \in R^{2kxd} P∈R2kxd表示所有层之间共享的相对位置嵌入向量(即,在向前传播期间保持固定),以及 Q r Q_r Qr和 K r K_r Kr分别是使用投影矩阵 W q , r , W k , r , W v , r ∈ R d x d W_{q,r}, W_{k,r}, W_{v,r}\in R^{dxd} Wq,r,Wk,r,Wv,r∈Rdxd生成的投影相对位置向量。
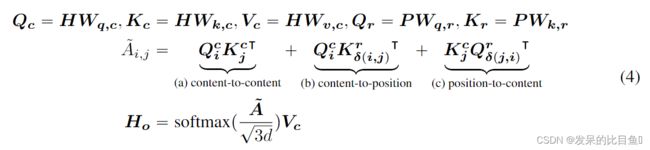
A i , j ~ \widetilde{A_{i,j}} Ai,j 是注意力矩阵 A ~ \widetilde{A} A 的元素,表示从token i i i到token j j j的注意力得分。 Q i c Q^c_i Qic是 Q c Q_c Qc的第 i i i行。 K j c K^c_j Kjc是 K c K_c Kc的第 j j j行。 K δ ( i , j ) r K^r_{\delta(i,j)} Kδ(i,j)r 是关于相对距离 δ ( i , j ) \delta(i,j) δ(i,j) 的 K r K_r Kr的第 δ ( i , j ) \delta(i,j) δ(i,j)行。 Q δ ( j , i ) r Q^r_{\delta(j,i)} Qδ(j,i)r是关于相对距离 δ ( j , i ) \delta(j,i) δ(j,i) 的 Q r Q_r Qr的第 δ ( j , i ) \delta(j,i) δ(j,i)行。请注意,此处我们使用 δ ( j , i ) \delta(j,i) δ(j,i)而不是 δ ( i , j ) \delta(i,j) δ(i,j)。 这是因为对于给定的位置 i i i,位置到内容计算是对于 i i i处的query位置和 j j j处的 k e y key key内容的注意力权重,因此相对距离为 δ ( j , i ) \delta(j,i) δ(j,i) 。 位置到内容的计算公式为 K j c Q j , i r K^c_jQ^r_{j,i} KjcQj,ir。 内容到位置的计算方法与此类似。
最后,我们将缩放因子 1 3 d \frac{1}{\sqrt{3d}} 3d1应用在 A ~ \widetilde{A} A 上。 该因子对于稳定模型训练非常重要(Vaswani,2017),尤其是对于大型PLM。

EFFICIENT IMPLEMENTATION
对于长度为 N N N的输入序列,需要 O ( N 2 d ) O(N^2d) O(N2d)的空间复杂度(Shaw,2018; Huang等人,2018; Dai,2019)来存储每个token的相对位置嵌入。 但是,以内容到位置为例,我们注意到由于 δ ( i , j ) ∈ [ 0 , 2 k ) \delta(i,j) \in [0,2k) δ(i,j)∈[0,2k)和所有可能的相对位置的嵌入始终是 K r ∈ R 2 k x d K_r \in R^{2kxd} Kr∈R2kxd的子集,因此我们可以对于所有quiries在注意力计算中重用 K r K_r Kr。
在我们的实验中,我们将最大相对距离k设置为512,以进行预训练。可以使用算法1高效地计算出解耦的注意力权重。令δ是根据等式3的相对位置矩阵,即 δ [ i , j ] ) = δ ( i , j ) \delta[i,j])=\delta(i,j) δ[i,j])=δ(i,j),我们没有为每个query分配不同的相对位置嵌入矩阵,而是将每个query向量 Q c [ i , : ] Q_c[i,:] Qc[i,:]乘以 K r T ∈ R d x 2 d K^T_r \in R^{dx2d} KrT∈Rdx2d ,如第3-5行所示。然后,我们使用相对位置矩阵δ作为索引,如第6-10行中所示。为计算位置到内容的注意力得分 A ~ p → c [ : , j ] \widetilde{A}_{p \rightarrow c}[:,j] A p→c[:,j],即注意力矩阵 A ~ p → c \widetilde{A}_{p \rightarrow c} A p→c的列向量,如第11-13行所述,通过 Q r T Q^T_r QrT乘以每个key向量 K c [ j , : ] K_c[j,:] Kc[j,:]。最后,如第14-18行那样,我们通过相对位置矩阵 δ δ δ提取相应的注意力得分作为索引。不需要分配内存来存储每个query的相对位置嵌入,从而降低了空间复杂度 O ( k d ) O(kd) O(kd)(对于存储 K r K_r Kr和 Q r Q_r Qr)。
ENHANCED MASK DECODER ACCOUNTS FOR ABSOLUTE WORD POSITIONS(绝对单词位置的增强型mask解码器)
DeBERTa是使用MLM进行预训练的,在该模型中,模型被训练为使用mask token周围的单词来预测mask词应该是什么。 DeBERTa将上下文的内容和位置信息用于MLM。 解耦注意力机制已经考虑了上下文词的内容和相对位置,但没有考虑这些词的绝对位置,这在很多情况下对于预测至关重要。
给定一个句子“a new store opened beside the new mall”,并用“store”和“mall”两个词mask以进行预测。 仅使用局部上下文(例如,相对位置和周围的单词)不足以使模型在此句子中区分store和mall,因为两者都以相同的相对位置在new单词之后。 为了解决这个限制,模型需要考虑绝对位置,作为相对位置的补充信息。 例如,句子的主题是“store”而不是“mall”。 这些语法上的细微差别在很大程度上取决于单词在句子中的绝对位置。
有两种合并绝对位置的方法。 BERT模型在输入层中合并了绝对位置。 在DeBERTa中,我们在所有Transformer层之后将它们合并,然后在softmax层之前进行mask token预测,如图2所示。这样,DeBERTa捕获了所有Transformer层中的相对位置,仅将绝对位置用作补充信息。 解码被mask的单词时。 因此,我们将DeBERTa的解码组件称为增强型Masked解码器(EMD)。 在实证研究中,我们比较了合并绝对位置的这两种方法,并观察到EMD效果更好。 我们推测,BERT所使用的绝对位置的早期合并可能会不利地阻碍模型学习足够的相对位置信息。 此外,EMD还使我们能够引入除位置以外的其他有用信息,以进行预训练。 我们将其留给以后的工作。
除NLU任务外,DeBERTa还可以扩展为处理NLG任务。 为了使DeBERTa像自回归模型一样操作以生成文本,我们使用了一个三角形矩阵进行self-attention,并按照Dong(2019)的方法将self-attention Masked的上三角部分设置为负无穷。
SCALE INVARIANT FINE-TUNING
本节介绍了一种新的虚拟对抗训练算法, Scale-invariant-Fine-Tuning 不变微调(SiFT),它是Miyato(Jiang et al2020)中描述的算法的一种变体,用于微调。
虚拟对抗训练是一种改进模型泛化的正则化方法。 它通过对抗性样本提高模型的鲁棒性,对抗性样本是通过对输入进行细微扰动而创建的。 对模型进行正则化,以便在给出特定于任务的样本时,该模型产生的输出分布与该样本的对抗性扰动所产生的输出分布相同。
对于NLP任务,扰动将应用于单词嵌入,而不是原始单词序列。 但是,嵌入向量的value范围(范数)在不同的单词和模型之间有所不同。 对于具有数十亿个参数的较大模型,方差会变大,从而导致对抗训练有些不稳定。
受层归一化的启发(Ba et al.,2016),我们提出了SiFT算法,该算法通过应用扰动的归一化的词嵌入来提高训练稳定性。 具体来说,在我们的实验中将DeBERTa微调到下游NLP任务时,SiFT首先将单词嵌入向量归一化为随机向量,然后将扰动应用于归一化的嵌入向量。 我们发现,归一化大大改善了微调模型的性能。 对于较大的DeBERTa模型,此改进更为突出。 我们将SiFT的全面研究留给未来的工作。
CONCLUSIONS
本文介绍了一种新的模型架构DeBERTa(注意力解耦的增强解码的BERT),它使用两种新颖的技术改进了BERT和RoBERTa模型。 首先是解耦的注意力机制,其中每个单词分别使用两个编码其内容和位置的向量表示,单词间的注意力权重分别使用解耦的矩阵计算其内容和相对位置。 其次是增强的mask解码器,它在解码层中合并了绝对位置,以在模型预训练中预测被mask的token。 此外,一种新的虚拟对抗训练方法用于微调,以改善模型对下游任务的概括。
我们通过全面的实证研究表明,这些技术显着提高了模型预训练的效率和下游任务的性能。 具有15亿个参数的DeBERTa模型就macro-average得分而言,首次超过了SuperGLUE基准的人类表现。
DeBERTa在SuperGLUE上超越人类的表现标志着通向通用AI的重要里程碑。 尽管在SuperGLUE上取得了令人鼓舞的结果,但该模型绝不能达到NLU的人文水平。 人类非常善于利用从不同任务中学到的知识来解决一项新任务,而无需或几乎没有特定任务的演示。 这被称为组合的综合,即对熟悉的组合的(子任务或基本的解决问题的技能)进行新组合的(新任务)的能力。 展望未来,值得探索如何使DeBERTa以更明确的方式组成合成结构,允许结合自然语言的神经和符号计算,去做类似于人类所做的事情。