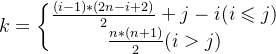数据结构 第四章 串、数组和广义表 学习笔记
目录
一、串
4.1 串的定义
4.2 串的存储
4.3 串的匹配
4.3.1 BF算法(暴力)
4.3.2 KMP算法
4.3.3 字符串哈希
4.4 注意
二、数组
4.1 数组的类型定义
4.2 数组的存储
4.3 特殊矩阵的压缩存储
4.3.1 对称矩阵
4.3.2 三角矩阵
4.3.3 对角矩阵
三、广义表
4.1 广义表的定义
4.2 广义表的操作
4.3 广义表的存储
4.3.1 头尾链表的存储结构
4.3.2 扩展线性链表的存储结构
一、串
4.1 串的定义
串(string)(或字符串)是由零个或多个字符组成的有限序列,一般记为
![]()
其中s为串的名字,其中元素可以是字母、数字或其他字符;传中字符的数目n称为串的长度,零个字符的串称为空串,其长度为0。
在C语言中,我们常常用char s[ ]的形式来表示一个串,而在C++中当调用了头文件#include
4.2 串的存储
串的存储有两种方式,顺序存储和链式存储,由于串作为一种一对一的逻辑结构(也就是线性结构),它的声明和存储模式就是一种线性表,而线性表的存储和操作已经在第二章讲的差不多了,就不再在这里赘述了。
4.3 串的匹配
说到串,最经典的一类题就是字符串匹配问题了,在这里放一道例题和三种解法:
4.3.1 BF算法(暴力)
这种算法最为直观,简单来说就是运用双指针对每一位进行比较,这时,时间复杂度为O(n*m)
#include
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 100;
const int mod = 1e9 + 7;
void solve()
{
string x,y;
cin>>x>>y;
int len=y.length();
x=x+x;
for(int i=0;i=x.length())
{
f=1;
break;
}
if(x[p]!=y[k])
{
f=1;
break;
}
}
if(!f)
{
cout<<"Yes\n";
return;
}
}
}
}
cout<<"No\n";
}
signed main()
{
int t;
cin>>t;
while(t--)
{
solve();
}
} 4.3.2 KMP算法
简单来说就是在BF算法的基础上加了一点记忆化搜索,减少了重复查找一段已经确认相同的子串,使得复杂度降为O(n+m)
4.3.3 字符串哈希
就是将每一段字符串看作一个高进制的数字(哈希值),然后通过匹配哈希值的方式来查找相同子串,复杂度为O(n-m),但是有时出题人可能卡哈希(即两个不同的字符串,在经过取模后哈希值相同),因此经常需要用到双哈希(据wls说双哈希也有人卡,他曾用过三哈希)。
4.4 注意
区分一下子串和子序列的概念:子串指的是串中连续的某一段;子序列则指的是需要按照串的序列但是不一定要连续的串。
另外,在串中的比较我们通常说的是字典序比较。在字典中,我们查询一个单词或者一个字往往都要以它的单词(或拼音)在26个字母中的排序来查找,这也就是字典序的由来,当串中不仅仅包括字母时,它的比较往往遵循ACII表每个字符的对应值来进行比较。
在串中,空串指的是长度为0的串,而不是有空格的串,在串中,空格也被看作一个符号。
二、数组
4.1 数组的类型定义
数组是由类型相同的数据元素构成的有序集合,每个元素称为数组元素,每个元素受n个线性关系的约束(这里的n指的是数组的维度不是数组长度)。
4.2 数组的存储
之前在第一章也说了,由于数组本身自带了这种一对一的逻辑关系(线性结构),且数组一般不发生插入和删除操作,所以都采用顺序存储的方式,这样可以更加直观的表达元素之间的关系。
而正是因为这一种顺序存储的方式,我们可以在O(1)的时间内完成对数组内任意位置元素的访问(又称随机存取结构),具体完成方式即是第一章所说的计算地址的方式。
4.3 特殊矩阵的压缩存储
由于矩阵在日常生活中较为常用,而很多特殊矩阵有很多相同元或是仅仅需要存储部分位置的元素,为了节省空间,于是便有了压缩存储
4.3.1 对称矩阵
由于对称矩阵元素关于对角线对称(即满足![]() ),那么我们可以用一个一维数组来存储,数组每个位置存储元素位置关系如下:
),那么我们可以用一个一维数组来存储,数组每个位置存储元素位置关系如下:
4.3.2 三角矩阵
几乎与对称矩阵存储方式一样,以主对角线划分,存在上三角矩阵和下三角矩阵,除了对角线的另一半元素只要相同,那么我们就可以将相同那一半元素只用一个存储单位存储,另一半按照对称矩阵的公式存储。
1)上三角
2)下三角
4.3.3 对角矩阵
对角矩阵所有非零元都能几种在以主对角线为中心的带状区域
总而言之,能用压缩存储的矩阵往往为稀疏矩阵,以上为三种比较典型的例子。
三、广义表
4.1 广义表的定义
广义表是线性表是线性表的推广,也称为列表,广义表一般记作
![]()
在广义表中,我们往往认为表中的每个既可以是广义表也可以是一个元素,而我们常常用大写字母代表广义表,小写字母代表单个元素。
4.2 广义表的操作
由于广义表的结构复杂且多变,所以广义表主要只有两个操作:取表头和表尾。
表头可以是单个元素也可以是一个广义表,但是表尾是去除表头之外其余元素组成的表,即表尾一定为一个广义表。
注意:广义表中()代表空表,长度为0,(())代表长度为1,有一个元素为空表,此时表头表尾都是空表()。
4.3 广义表的存储
由于广义表每个元素存储的元素并不统一,并不适用顺序存储,主要用两种链式存储。
4.3.1 头尾链表的存储结构
由前面的定义我们可以发现,只要确定了一个表的表头和表尾,那么一个表也就确定了,并且由于表中元素只有原子和广义表两种,因此需要两种结点:表结点和原子结点。
4.3.2 扩展线性链表的存储结构
唯一区别在于所有结点都是由三个域组成:指示表头的指针域,指示表尾的指针域和值域。
广义表的深度是指广义表中展开后所含括号的层数,广义表的长度是指广义表中所 含元素的个数。