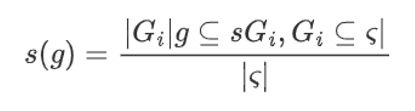数据挖掘之子图模式

---

子图模式概述

图和子图

• 图的结构很简单，就是由顶点V集和边E集构成，因此图可以表示成：G=(V,E)。

• 子图是一个图中的一部分，其可以表示为：

• 子图模式：是用来提取图数据库中的频繁子结构的一种模式。子图关系可以表示为：G′⊆ sG。

频繁子图

如何判断某子图是频繁子图？

支持度:给定图的集族ς, 子图g的支持度定义为包含它的所有图所占的百分比。

有了支持度的定义就可以计算某子图在图集中的占比，如此便可来规定频繁子图。

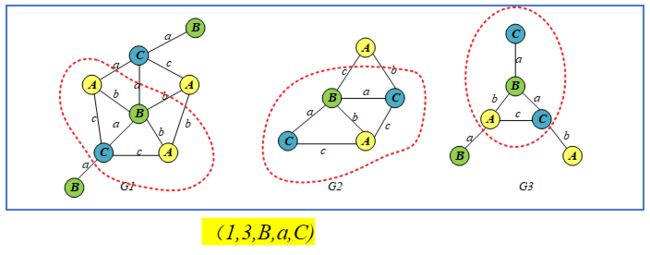
• 例子：计算子图g1, g2, g3在如下图数据集中的支持度

对频繁子图的搜索与查找也就称之为频繁子图挖掘。频繁子图挖掘(frequent subgraph mining) ：
给定集合 ς 和支持度阈值 minsup，频繁子图挖掘的目标是找出使得所有 s(G) ≥ minsup 的子图G。

目前常用的两种频繁子图挖掘的算法为 Apriori 与 gSpan。接下来将分别介绍无向有权图的 Apriori 与 gSpan算法。

---

类Apriori算法

Apriori algorithm是关联规则里一项基本算法。由Rakesh Agrawal 在 1994年提出的，详细的介绍来自于《Fast Algorithms for Mining Association Rules》。

关联规则

关联规则形如“如果…那么…(If…Then…)”，前者为条件，后者为结果。

关联规则的目的在于在一个数据集中找出项之间的关系，也称之为购物篮分析 (market basketanalysis)。

例如，购买鞋的顾客，有10%的可能也会买袜子，60%的买面包的顾客，也会买牛奶。这其中最有名的例子就是"尿布和啤酒"的故事了。

置信度与支持度

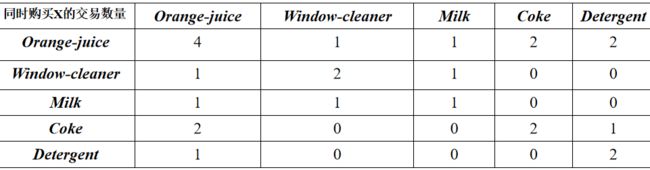
假设有如下表的购买记录

按照关联规则进行整理得到下表：

• 置信度：置信度表示了这条关联规则有多大程度上值得可信。
  设条件的项的集合为A,结果的集合为B。
  置信度计算在A中，同时也含有B的概率，即Confidence(A==>B)=P(B|A)。
  例如计算“如果Orange-juice则Coke”的置信度。由于在含有Orange-juice的4条交易中，仅有2条交易含有Coke，其置信度为0.5。

• 支持度：支持度计算在所有的交易集中，既有A又有B的概率。 Support(A and B)=P(AB)
  例如在5条记录中，既有Orange-juice又有Coke的记录有2条。则此条规则的支持度为2/5=0.4。
  现在这条规则可表述为，如果一个顾客购买了Orange-juice,则有50%的可能购买Coke 。而这样的情况（即买了Orange-juice会再买Coke ）会有40%的可能发生。

类Apriori算法步骤

1. 候选产生：合并频繁（k-1）子图对，得到候选k-子图。
2. 候选剪枝：丢弃包含非频繁的 (k-1) 子图的所有候选 k 子图。
3. 支持度计算：统计 ς 中包含每个候选的图的个数。
4. 候选删除：丢弃支持度小于minsup的所有候选子图。

候选产生

• 在候选产生阶段，合并 (k-1) 子图为 k 子图，首要问题是如何定义子图的大小 k。
  通过添加一个顶点，迭代地扩展子图的方法称作顶点增长（vertex growing）。
  k 也可以是图中边的个数，添加一条边到已有的子图中来扩展子图的方法称作边增长（edge growing）。

• 为了避免产生重复的候选，我们可以对合并施加条件：两个 (k-1) 子图必须共享一个共同的 (k-2) 子图，共同的子图称为核（core）。

• 由此，产生了两种子图候选产生的方法：

  • 顶点增长（vertex growing）
  • 边增长（edge growing）

顶点增长

通过添加一个新的结点到已经存在的一个频繁子图上来产生候选。可以使用邻接矩阵来表示图，每一项M(i, j)为链接vi和vj的的边或者0。

边增长

边增长将一个新的边插入到一个已经存在的频繁子图中。
与顶点增长不同，结果子图的顶点个数不一定增长。

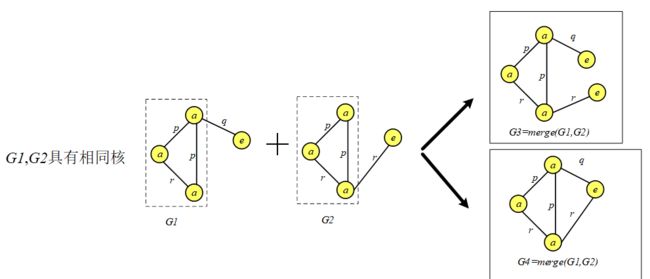
边增长合并过程：一个频繁子图 g1 和另一个频繁子图 g2 合并，仅当从 g1 删除一条边后得到的子图与从 g2 中删除一条边后得到的子图的拓扑等价，合并后的结果是 g1 添加 g2 那条之外的边。

候选剪枝

• 候选剪枝需要剪去(k-1)子图非频繁的候选。可以通过以下方式实现：相继从 k 子图中删除一条边，并检查得到的(k-1) 子图是否连通且频繁。如果不是，则该候选 k 子图可以丢弃。意思是一次删除一条，总共有 k 个子图要检测。

• 为了检查(k-1)子图是否频繁，需要将其与其他的(k-1)子图匹配，此时需判定两个图是否拓扑等价，即处理图同构的问题。

如何处理图同构

• 处理图同构的问题的标准方法是，将每个图都映射到一个唯一的串表达式，称作代码或规范标号(canonical label)。如果两个图是同构的，则它们的代码一定相同。这个性质可以使得我们通过比较图的规范编号来检查图同构。
• 构造图的规范标号的步骤如下：
  1. 找出图的邻接矩阵表示。可利用矩阵中的基本矩阵进行行列互换。
  2. 确定每个邻接矩阵的串表示，由于邻接矩阵是串表示的，因此只需要根据矩阵的上三角阵部分构造串就足够了。
  3. 比较图的所有串表示，并选出具有最小（最大）字典序值的串，确保每个图的字符串唯一。

支持度计算

当我们剪枝完成之后，将剪枝后剩余的候选图进行支持度计算，将其中大于支持度阈值的候选图记为满足条件的频繁子图。

候选删除

对于所有频繁的候选子图，还需要进行图的同构测试，以减除重复的频繁候选子图。

类Apriori算法总结

类Apriori方法在每一层频繁子图的挖掘过程中，算法都会产生大量的非频繁的候选子图。
然后对候选的频繁子图执行支持度计数。
对于所有频繁的候选子图，还需要进行图的同构测试，以减除重复的频繁候选子图。
因为图的同构测试是一种NP完全问题，所以对于大规模的频繁子图进行图的同构测试是一个开销很大的过程，甚至是不可能完成的任务。
因此，大量生成的候选子图和图的同构测试的巨大开销是Apriori类方法的性能瓶颈。

---

gSpan算法

gSpan 算法通过执行最右扩展的策略减少了候选子图重复的产生，同时也保证了搜索结果的完备性。

gSpan 算法设计出一种新式的图的规范标号，将图的同构测试与重复图的检测结合到一块，避免了在已经获得的频繁子图集合中搜索重复图。

DFS编码

• 为了遍历图，gSpan算法采用深度优先搜索。
• 初始，随机选择一个起始顶点，并且对图中访问过的顶点做标记。
• 被访问过的顶点集合反复扩展，直到建立一个完全的深度优先搜索 (DFS) 树。
• DFS编码采用五元组的方式进行表示(vi , vj , A, a, B)，其中vi , vj 表示点的ID；
  A，B表示点的标号；
  a 为A, B点之间边的标号。

确定唯一DFS编码

一个图可能有多个DFS编码。选择其中最小的DFS编码作为唯一编码。例：

比较 g1(X,a,Y)、g2(Y,a,X)与g3(X,a,X)
按照字典序比较字符串(A 则可以得出g3(X,a,X)> g1(X,a,Y)> g2(Y,a,X)

gSpan最右路径扩展规则

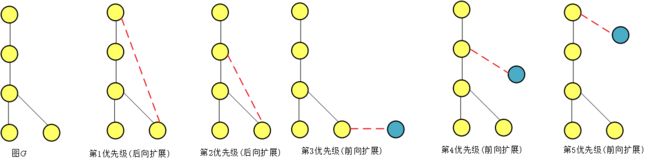
• 给定图G 和G 的DFS树T ，一条新边 e 可以添加到最右节点和最右路径上另一个节点之间（后向扩展）.
• 或者可以引进一个新的节点并且连接到最右路径上的节点（前向扩展）。
• 由于这两种扩展都发生在最右路径上，因此称为最右扩展。

gSpan算法步骤

1. 遍历所有的图，计算出所有的边和点的频度。
2. 将频度与最小支持度数做比较，移除不频繁的边和点。
3. 重新将剩下的点和边按照频度进行排序，将他们的排名号给边和点进行重新标号。
4. 再次计算每条边的频度，计算完后，然后初始化每条边，并且进行此边的subMining()挖掘过程。subMining过程如下：
   1. 根据graphCode重新恢复当前的子图。
   2. 判断当前的编码是否为最小DFS编码，如果是加入到结果集中，继续在此基础上尝试添加可能的边，进行继续挖掘。
   3. 如果不是最小编码，则此子图的挖掘过程结束。

gSpan算法示例

1. gSpan算法图集输入：

图集中共有14个A顶点，8个B顶点，7个C顶点。15条a边，13条b边，8条c边。

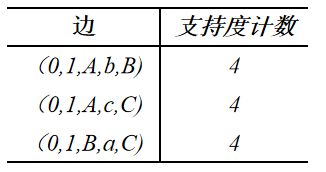
2. 遍历所有的图，计算出所有的边和点的频度：

3. 这三条边为频繁子图开始，以其中一条边开始扩展，因为这些边是频繁的，所以后面在频繁子图出现的边也必须是这三条边中的一条。

4. 选择 support >= 3 的继续扩展

5. 将符和的候选边加入继续进行拓展

6. 基于优先级规则的下一步是尝试将唯一常用边(C, c, A) 做连接

此次得到的结构仅存在于其中的一个图表中，因此将进入下一个增长优先级。
由于v3与v1已经存在连接，故第二优先级不再适用，因此尝试再次从v3增长/延伸，由此可以添加（C，a，B）或（C，c，A）。

7. 尝试添加（C，c，A）。但在留下的任何图表中都找不到它。
   由于在这里再次走向死胡同，将进入第五个优先增长选择：再次从根增长。
   如果试图从根v0增长，可以使用（A，b，B）或（A，c，C）。
   从（A，b，B）开始，将得到一个如下所示的子图

这在(G1-G5)的任何图表中都找不到，所以添加（A，c，C）作为最后的尝试

添加（A，c，C）后得到的子图，在(G1-G5)的找不到表明该结构增长终止。

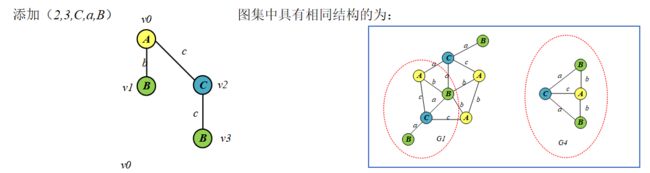
8. 回到最近一个待定状态（1,3,B,b,A），其support<3，继续回到（3,0,C,c,A）support<3，继续回到上一个待定状态(2,0,C,c,A)，如下:

图集中具有相同结构的为：

9. 此时可以从C节点扩展，我们的两个选项是（2,3,C,a,B）和（2,3,C,c,A）

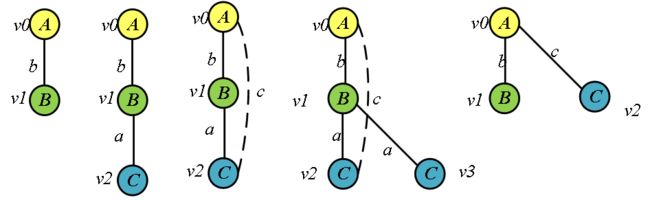
10. 至此第一条边扩展结束得到的频繁子图为

11. 第一条边扩展结束，依次扩展第二条边（0,1,A,c,C）并在原图中去掉(A,b,B)边。

扩展过程如边（0,1,A,b,B）相同，扩展之后得到的频繁子图为

12. 第二条边扩展结束，依次扩展第三条边（0,1,B,a,C）并在原图中去掉(A,b,B)与(A,c,C)边。扩展之后得到的频繁子图为

13. 至此遍历完了右表中的全部边，得到了所有的频繁子图，如下：

gSpan算法小结

• gSpan算法总的思想大致为，先生成频繁树，再在频繁树的基础上，生成频繁子图，满足最小支持度，满足最小DFS编码的所有频繁子图。

• gSpan 算法通过执行最右扩展的策略减少了候选子图重复的产生，同时也保证了搜索结果的完备性。

• gSpan 算法设计出一种新式的图的规范标号，将图的同构测试与重复图的检测结合到一块，避免了在已经获得的频繁子图集合中搜索重复图。