算法通过村第三关-数组基础笔记|爱不起的数组
文章目录
- 前言
- 线性表的概念
-
- 什么是线性表
-
- 从语言实现的角度看
- 从存储的角度看
- 从访问限制的角度看
- 从扩容的角度看
- 数组的概念
- 数组元素的特征
- 数组的基本操作
-
- 数组的创建和初始化
- 查找一个元素
- 增加一个元素
- 删除一个元素
- 总结
前言
提示:孩子们有时候挺伤人的,他们以为只要你恰好是个大人,你就刀枪不入,怎么也不会受伤。
谈起数组,都是令人头疼的问题,恶心的临界判断
当然了这里不是吐槽的,我们要把数组这一块学会的,还是一步一步的来吧,先补习一下知识:
- 什么是线性表
- 数组的概念
- 数组元素的存储特征
线性表的概念
什么是线性表
先来谈谈常见的数据结构:

Q:当然了这就要问了,什么是线性表?
A:所谓的线性表就是具有相同特征元素的一个有限序列,其中所含元素的个数成为线性表的长度。
我们从多角度分析一下:
从语言实现的角度看
从存储的角度看
可分为顺序型和链表型:
顺序型:就是将数据存放在一段固定的区间内,此时访问元素的效率非常高,但是删除和增加元素的代价比较大,如果想扩容只能整体搬迁。
链表型:元素之间是通过地址依次连接的,因此访问时必须要从头开始逐步向后找,所以说查找的效率低,删除和增加的效果非常好,并不需要考虑扩容的问题。常见的链表实现方式:单链表,循环链表,双链表等等。
从访问限制的角度看
栈和队列又被称为访问受限的线性表,插入和删除受到了限制,只能在固定的位置进行。而Hash比较特殊,其内部真正存储数据的一般是数组,但是访问是通过映射来实现的,因此大部分材料里面比不将Hash归结到线性表中。
线性表的知识框架图:
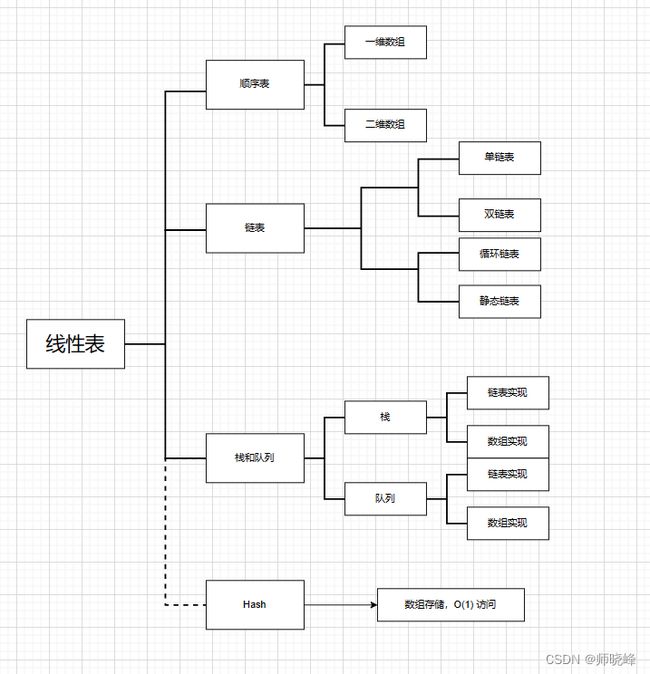
线性表的常见问题:初始化、求表长、增删改查等、其本质就是上面的每种数据结构至少要有这几中操作,当然大部分的算法题目也是基于此扩展的。
从扩容的角度看
采用分离式结构的顺序表,若将数据更换为存储空间更大的区域,则可以在不改变表对象的前提下对其数据存储区进行扩容,所有使用这个表的地方都不必修改。只要程序的要运行环境(计算机系统)还有剩余,这种表结构就不会因为满了而导致无法进行操作。人们把采用这种技术实现的顺序表称为动态顺序表,因为其容量可以在使用中动态变化。
扩容的两种策略:
- 每次扩容增加固定的数目的存储位置,比如每次扩充10个元素位置,这种策略可以称为线性增长。特点是:节省空间,但是扩充操作频繁,操作次数多。
- 每次扩容容量加倍,比如每一次扩充增加一倍存储空间。特点是:减少了扩充操作的执行次数,但是可能会造成浪费空间资源。典型的以空间换时间,推荐的方式。(java)
数组的概念
数组是线性表最基本的结构,特点是元素是一个紧密在一起的序列,相互之间不需要记录彼此的关系就能访问,比如月份,星球等。
数组用索引的数组来标识每项数据在数组中的位置,且在大多数编程语言中,索引是从0 算起的。我们可以通过索引快速定位到数组中的元素。

数组有两点需要注意的:
- 索引从0开始 及第一个 存储元素的位置是a[0],最后一个存储元素的位置是a[length-1]。
- 数组中的元素在内存中是连续存储的,且每个元素占用相同的大小内存。
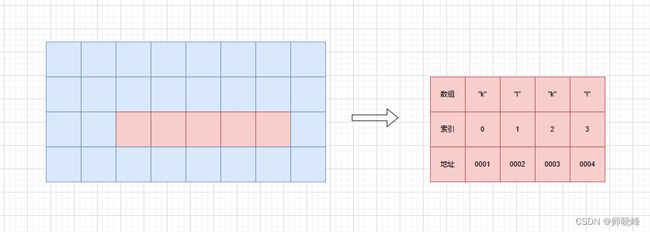
注意:数组空间不一定是满的,100的空间可能只用了10个位置,所以要注意数据个数的变化size和数组长度length可能不一样。
数组元素的特征
数组中的经典问题:
Q:我创建了一个大小为10的数组,请问此时数组里面是什么?
A:在Java里面,会默认初始化为0.
Q:是否可以只初始化一部分位置?初始化的本质是什么?
A:当然可以,你可以将前面5个位置赋值,后面的空着。比如数组内容{1,2,3,4,5,0,0,0,0,0}.初始化的本质就是覆盖已有的值,你需要的值覆盖原来的0,因为数组本来是{0,0,0,0,0,0,0,0,0,0}.这里只是做了替换。因此你想要知道有效元素的个数,就必须有一个额外的变量,例如size来标记。
Q:那么上面已经初始化的元素之间是否可以空着,比如这样{1,0,0,2,0,3,8,3,9},0表示还没有初始化的数据。
A:不可以! 当然不可以这么做。要初始化,就必须从前向后的连续空间初始化,不可以出现空缺的情况,这里违背数组的原则。你在进行某种运算期间可以先给一部分位置赋值,而一旦稳定了,就不再可能在出现空位置的情况。
Q:如果我需要的数据在中间的某一段该怎么办?比如{0,0,0,3,4,5,5,67,0,0,0},此时我想获取3-67的元素呢?
A:你需要使用两个变量,例如left = 3 ,right = 7 来表示区间[left,right]是有效的。
Q:我删除的时候,已经被删除的位置该是什么呢?例如原始数组为{1,2,3,4,5,0,0},我删除了4之后,根据数组的移动原则,从4开始向前移动,变成{1,2,3,5, ?,0,0},原来5的位置应该是什么呢?
A:还是5,也就是删除4之前的结构是{1,2,3,5, 5,0,0},此时便是元素数量的size会建议变成4,原来5的位置还是5,因为我们是通过size来标记元素数量的,所以最后一个5不会呗访问到。
Q:这里的5看起来不好看,可以用来再优化一下?
A:不必要,没啥用。
数组的基本操作
当然在面试中,大多使用int类型,所以这里我们就使用int来举例啦
数组的创建和初始化
int[] arr = new int[10];
数组最基础的初始化就是循环赋值
for(int i = 0; i < arr.length, i++)
arr[i] = i;
但是这种方式在面试题中一般不行,因为很多题目会给出若干测试数据组让你都能测试通过,比如给你[0,1,2,3,4,5,6]和[0,3,4,5,6,1]。这样的时候怎么初始化最优呢?
显然这里不能使用循环了,too low,可以试试一下的写法
int[] arr = new int[]{0,1,2,3,4,5,6};
// 也可以这样写
int[] arr = {0,3,4,5,6,1};//背下来 记住 ⭐⭐⭐⭐⭐
这样的化,如果测试第二组数据,直接将其替换就行,并且简单方便,在面试中也是比较常用的,牢记⭐,
注意:创建数组时大小就是元素的数量,是无法再插入元素的,如果你需要增加新的元素就不能这么用。
查找一个元素
我们探讨一下为什么数组的题目这么多呢?
其实多数题目的本质实在查找问题,而数组时查找的最佳载体。很多复杂的算法都是为了提高查询效率的,比如二分查找,二叉树,红黑树,B+树,Hash和堆等等。另一方面很多算法的本质也是查找问题,就比如滑动窗口问题,回溯问题,动态规划问题等待都是再寻找目标结果。
这里简单的写一个等值查找,实现如下:
/**
* @param arr
* @param size 已经存放的元素容量
* @param key 待查找的元素
* @return
*/
public static int findByElement(int[] arr, int size, int key) {
// 参数校验
if (arr == null || size == 0) {
return -1;
}
for (int i = 0; i < size; i++) {
if (arr[i] == key) {
return i;
}
}
return -1;
}
增加一个元素
增加和删除元素时数组最基本的操作,看别人的代码很容易,但是自己写代码的时候,你就知道了“纸上谈兵”。能准确的处理游标和边界等情况是数组算法最基础重要的问题之一。所以当然需要自己亲手写一边才可以,不要觉得简单就不去做,当真正用的时候才后悔,这样得不偿失。
将给给定的元素插入到有序的数组的对应位置中,我们可以先找到位置,然后再其后的元素整体右移,最后插入到空位上。这里需要注意的是,算法必须保证在数组的首部,尾部,中部插入都可以成功。问题貌似采用一个for循环就可以解决,但是当你写出来运行时,傻眼了☠️,各种bug出现,很恶心。
推荐一种方式,你可以这样写⭐。(保证数组的单调性)
/**
* @param arr
* @param size 数组已经存储的元素数量
* @param element 待插入的元素元素
* @return
*/
public static int addByElementSequence(int[] arr, int size, int element) {
// 校验参数
if (arr == null || arr.length == 0) {
return -1;
}
// 这里不能是 大于 等于的时候也是
// 数组的下标是从 0 开始的
// size 记录有效元素 1 开始的 arr.length 记录数组的长度 从 1 开始
if (size >= arr.length) {
return -1;
}
//这里是为了保持单调性 即 index != 0/arr.length - 1
int index = size;
// 找到新元素插入的位置
for (int i = 0; i < size; i++) {
if (element < arr[i]) {
index = i;
break;
}
}
// 元素后移
for (int j = size; j > index; j--) {
arr[j] = arr[j - 1]; // index下标的元素后移一个位置
}
arr[index] = element;
return index;
}
删除一个元素
对于删除元素,不可以一边遍历一边查找,因为元素可能不存在。所以要分为两个步骤,先检查元素是否存在元素,存在再删除。
需要考虑多种情况,首部,中部,尾部,不存在都要有效,推荐这样写
/**
* 遍历数组,如果发现目标元素,则将其删除,
* 数组的删除就是从目标元素开始,用后续元素依次覆盖前继元素
*
* @param arr 数组
* @param size 数组中的元素个数
* @param key 要删除的目标值
*/
public static int removeByElement(int[] arr, int size, int key) {
// 参数校验
if (arr == null || arr.length == 0){
return -1;
}
int index = -1;
// 找到要删除元素的位置
for (int i = 0; i < size; i++) {
if (arr[i] == key) {
index = i;
break;
}
}
if (index != -1) {
for (int j = index + 1; j < size ; j++) {
arr[j - 1] = arr[j];
}
size--;
}
return size;
}
总结
提示:不要觉得数组很简单,真的自己写一写才知道。
