GhatGPT实现 泰坦尼克号生存预测

ChatGPT 实现泰坦尼克号生存预测

1.引言

1.1 研究背景

泰坦尼克号是一次历史上著名的海难事件，发生在1912年，造成了大量乘客的伤亡。数据集来源于Kaggle竞赛中的"Titanic: Machine Learning from Disaster"，提供了关于乘客的各种信息。本研究的目标是通过分析乘客的特征和生存情况之间的关系，建立模型来预测乘客的生存情况。

1.2 数据集介绍

数据集包括训练集（train.csv）和测试集（test.csv）两部分。训练集包含了乘客的特征信息，如船舱等级、性别、年龄等，以及乘客的生存情况（存活与否）。而测试集除了没有乘客的生存情况属性，其他的属性都与训练集一致。

1.3 研究目的

本研究的主要目的是基于提供的数据集，构建一个预测模型，能够准确预测乘客的生存情况。此外，我们还将探索不同特征与乘客生存率之间的关系，并提出基于分析结果的相关建议。

2. 数据描述

2.1 数据来源

数据集来源于Kaggle竞赛中的"Titanic: Machine Learning from Disaster"，该竞赛旨在通过机器学习方法预测乘客的生存情况。

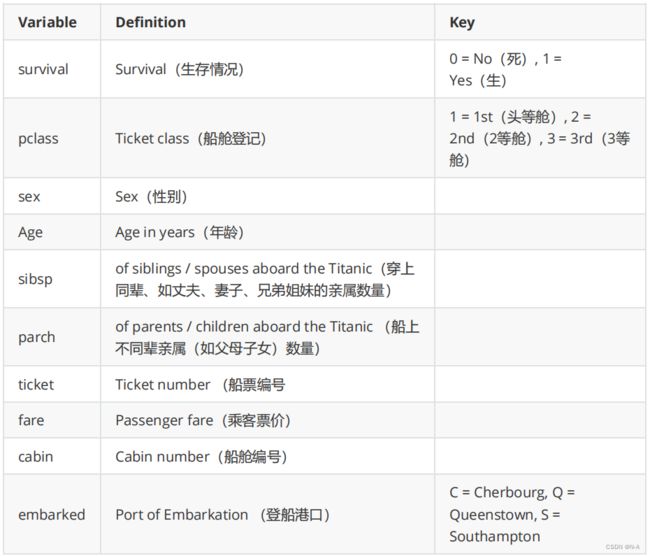
2.2 数据集结构和变量定义

提供的训练数据集包含以下变量：

2.3数据摘要和统计分析

此部分加载训练集和测试集数据，然后进行数据摘要和统计分析。数据集的基本统计特征提供了有关数据集中每个特征的分布、中心趋势和离散程度的信息。相关系数矩阵用于衡量特征之间的线性相关性，有助于了解特征之间的关系。

对应的设计代码如下：

import pandas as pd

# 导入训练集数据
train_data = pd.read_csv('train.csv')

# 导入测试集数据
test_data = pd.read_csv('test.csv')

# 获取数据集的基本统计特征
summary = train_data.describe()
print("数据集的基本统计特征：")
print(summary)

# 计算特征之间的相关系数矩阵
corr_matrix = train_data.corr()
print("\n特征之间的相关系数矩阵：")
print(corr_matrix)

在代码开头，导入了pandas库，它用于数据处理和分析。使用pd.read_csv()函数，从CSV文件中导入训练集和测试集数据，并将它们存储在train_data和test_data变量中。使用describe()函数计算了训练集数据的基本统计特征，并将结果存储在summary变量中。打印出基本统计特征，以便查看训练集数据的概要信息。使用corr()函数计算了训练集数据中特征之间的相关系数矩阵，并将结果存储在corr_matrix变量中。最后打印出相关系数矩阵，以便了解训练集数据中特征之间的相关性。

3. 数据处理

3.1 缺失值处理

此部分检查数据集中的缺失值情况，并对缺失值进行处理。对于训练集和测试集，首先计算各个变量的缺失值数量，然后针对缺失值进行填充处理。

处理缺失值是数据预处理的一个重要步骤，以确保数据的完整性和准确性。在此代码中，年龄列的缺失值使用均值填充，而登船港口和票价列的缺失值使用众数填充。

下面是使用Pandas库进行缺失值处理的示例代码：

# 检查缺失值
missing_values1 = train_data.isnull().sum()
print("各变量的缺失值数量：")
print(missing_values1)
missing_values2 = test_data.isnull().sum()
print("各变量的缺失值数量：")
print(missing_values2)

# 处理训练集缺失值：用均值填充年龄列的缺失值，用众数填充登船港口的缺失值
train_data['Age'].fillna(train_data['Age'].mean(), inplace=True)
train_data['Embarked'].fillna(train_data['Embarked'].mode()[0], inplace=True)

# 处理测试集缺失值：用均值填充年龄列的缺失值，用众数填充票价的缺失值
test_data['Age'].fillna(test_data['Age'].mean(), inplace=True)
test_data['Fare'].fillna(test_data['Fare'].mode()[0], inplace=True)

使用isnull().sum()函数计算训练集数据中各个变量的缺失值数量，并将结果存储在missing_values1变量中。使用print()函数打印出各个变量的缺失值数量，以便查看训练集数据中的缺失情况。类似地，使用isnull().sum()函数计算测试集数据中各个变量的缺失值数量，并将结果存储在missing_values2变量中。使用print()函数打印出各个变量的缺失值数量，以便查看测试集数据中的缺失情况。

使用fillna()函数，将训练集数据中’Age’列的缺失值用均值进行填充。均值通过调用mean()函数计算得到。将训练集数据中’Embarked’列的缺失值用众数进行填充。众数通过调用mode()[0]函数计算得到。

将测试集数据中’Age’列的缺失值用均值进行填充。均值通过调用mean()函数计算得到。将测试集数据中’Fare’列的缺失值用众数进行填充。众数通过调用mode()[0]函数计算得到。

3.2 特征工程

此部分创建一个新的特征’FamilySize’，该特征表示乘客的家庭大小。通过将’SibSp’和’Parch’相加，并加上1，计算出每个乘客的家庭成员数量。同时，对于分类特征’Sex’，使用LabelEncoder对其进行编码，将其转换为数值表示，以便后续的建模和分析。

这些步骤属于特征工程的一部分，旨在利用现有的特征创建新的有意义的特征，并对分类特征进行编码，以便机器学习算法能够处理。

下面是使用Pandas库进行特征工程的示例代码：

from sklearn.preprocessing import LabelEncoder

# 创建新特征：家庭大小
train_data['FamilySize'] = train_data['SibSp'] + train_data['Parch'] + 1
test_data['FamilySize'] = test_data['SibSp'] + test_data['Parch'] + 1

# 特征编码：性别
label_encoder = LabelEncoder()
train_data['Sex'] = label_encoder.fit_transform(train_data['Sex'])
test_data['Sex'] = label_encoder.transform(test_data['Sex'])

在训练集中，通过将’SibSp’（兄弟姐妹/配偶的数量）和’Parch’（父母/子女的数量）相加，再加上1，计算出每个乘客的家庭大小，并将结果存储在名为’FamilySize’的新列中。在测试集中，同样地，通过将’SibSp’和’Parch’相加，再加上1，计算出每个乘客的家庭大小，并将结果存储在名为’FamilySize’的新列中。

特征编码性别，首先，实例化一个LabelEncoder对象，该对象用于将分类特征进行编码。对训练集的’Sex’（性别）列进行编码，通过调用fit_transform()方法，将性别类别转换为数值编码，并将结果覆盖原来的’Sex’列。对测试集的’Sex’列进行编码，通过调用transform()方法，使用之前训练集上的编码器，将性别类别转换为数值编码，并将结果覆盖原来的’Sex’列。

3.3 数据标准化或归一化

侧部分对数据进行标准化和归一化，将不同特征的数值范围调整为统一范围，以消除特征间的量纲差异。

下面是使用Scikit-learn库进行数据标准化的示例代码：

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer

# 移除非数值类型的列，例如乘客姓名、船舱编号等
train_data.drop(['Name', 'Cabin', 'Ticket'], axis=1, inplace=True)
test_data.drop(['Name', 'Cabin', 'Ticket'], axis=1, inplace=True)

# 数据标准化
# 分离特征和目标变量

X_train = train_data.drop('Survived', axis=1)
y_train = train_data['Survived']

# 创建Pipeline来处理特征编码和数据标准化
# 列转换器：对非数值类型的列进行编码

categorical_features = ['Sex', 'Embarked']
categorical_transformer = Pipeline(steps=[
  ('encoder', OneHotEncoder())])  

# 列转换器：对数值类型的列进行标准化
numeric_features = ['Pclass', 'Age', 'SibSp', 'Parch', 'Fare', 'FamilySize']
numeric_transformer = Pipeline(steps=[('scaler', StandardScaler())])

# 使用ColumnTransformer将两个转换器结合起来
preprocessor = ColumnTransformer(
  transformers=[
    ('cat', categorical_transformer, categorical_features),
    ('num', numeric_transformer, numeric_features)
  ])

# 对训练集数据进行转换
X_train_scaled = preprocessor.fit_transform(X_train)

# 对测试集数据进行转换
X_test_scaled = preprocessor.transform(test_data)

# 划分训练集和验证集
from sklearn.model_selection import train_test_split
X_train_scaled, X_val, y_train, y_val = train_test_split(X_train_scaled, y_train, test_size=0.2, random_state=42)

# 输出标准化后的数据
print(X_train_scaled)
print(X_val)

上述代码中，我们使用ColumnTransformer将特征编码和数据标准化的转换器结合起来，并通过Pipeline进行流水线处理。首先，我们定义了针对非数值类型的列的独热编码转换器categorical_transformer和针对数值类型的列的标准化转换器numeric_transformer。然后，通过ColumnTransformer将这两个转换器组合起来，并定义了需要进行转换的列。最后，我们使用fit_transform方法对训练集数据进行转换，并使用transform方法对测试集数据进行转换。

3.4 数据集划分

在使用训练集进行模型训练之前，我们需要将训练数据集再次划分为训练集和验证集，用于评估模型的性能和调优。这样，在模型训练过程中可以使用验证集进行模型选择和参数调整。

下面是使用Scikit-learn库进行数据集划分的示例代码：

from sklearn.model_selection import train_test_split

# 将特征变量和目标变量分离
X = train_data.drop('Survived', axis=1)
y = train_data['Survived']

# 划分数据集为训练集和验证集
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)

此代码将训练数据集(train.csv)划分为训练集(X_train和y_train)和验证集(X_val和y_val)，用于模型训练和性能评估。

4. 数据分析

4.1 探索性数据分析

4.1.1 乘客生存率分析

此部分通过柱状图比较幸存者和非幸存者的人数。首先，使用value_counts()函数计算出’Survived’列中幸存者和非幸存者的人数统计结果。然后，使用plot()函数绘制柱状图，将幸存者和非幸存者作为x轴标签，人数作为y轴标签，以直观地显示两者之间的比较关系。

此部分对应的代码如下：

import matplotlib.pyplot as plt
import seaborn as sns

# 幸存者与非幸存者的人数比较
survived_count = train_data['Survived'].value_counts()
survived_count.plot(kind='bar', rot=0)
plt.xlabel('Survived')
plt.ylabel('Count')
plt.title('Survived vs. Count')
plt.show()

对应的结果如下图所示：

​ 图4-1 幸存与非幸存的人数柱状图

4.1.2 不同特征与生存率的关系分析

此部分分析性别与生存率的关系以及船舱等级与生存率的关系，并对其进行可视化。以便观察和分析特征对生存率的影响。使用sns.barplot()函数绘制条形图，其中x轴表示特征，y轴表示生存率，并使用训练集数据。然后，使用plt.xlabel()、plt.ylabel()和plt.title()分别设置x轴标签、y轴标签和图表标题。最后，使用plt.show()显示绘制的图表。

对应的设计代码如下：

# 性别与生存率的关系
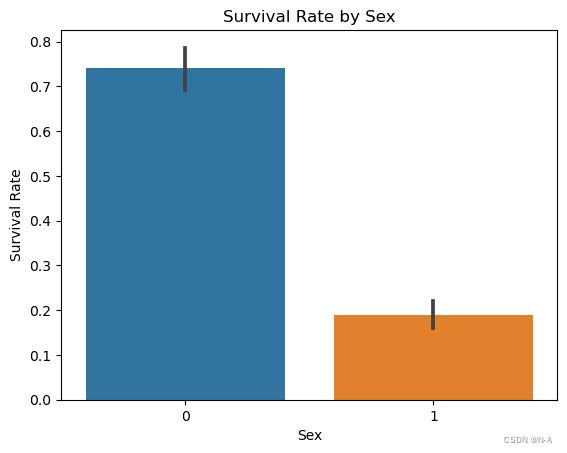
sns.barplot(x='Sex', y='Survived', data=train_data)
plt.xlabel('Sex')
plt.ylabel('Survival Rate')
plt.title('Survival Rate by Sex')
plt.show()

# 票价与生存率的关系
sns.barplot(x='Pclass', y='Survived', data=train_data)
plt.xlabel('Pclass')
plt.ylabel('Survival Rate')
plt.title('Survival Rate by Pclass')
plt.show()

对应的结果如下图所示：

​ 图4-2 性别与生存率的关系柱状图

图4-3 票价与生存率的关系柱状图

使用.corr()方法计算各个特征之间的相关系数矩阵。使用热力图可视化相关系数矩阵，观察各个特征之间的相关性强弱。

# 计算特征之间的相关系数
correlation = train_data.corr()

# 绘制特征相关性热力图
plt.figure(figsize=(10, 8))
sns.heatmap(correlation, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

对应的结果如下图所示：

​ 图4-4 特征相关性热力图

4.2 机器学习算法预测

可以选择逻辑回归、决策树、随机森林等算法进行模型训练和预测。使用训练数据集划分训练集和验证集，进行模型训练和交叉验证评估。使用评估指标（如准确率、精确率、召回率、F1-score）评估模型的性能。

4.2.1 模型选择与训练

在进行机器学习算法预测之前，我们需要选择合适的模型。根据问题的性质和数据集的特点，常用的模型包括逻辑回归、支持向量机、决策树、随机森林等。在本案例中，我们选择了随机森林分类器（RandomForestClassifier）作为预测模型。

下面是模型选择与训练的代码示例：

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

# 定义特征列
features = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'FamilySize']

# 实例化随机森林分类器
model = RandomForestClassifier()

# 训练模型
model.fit(X_train_scaled, y_train)

4.2.2 模型评估与优化

在训练模型后，我们需要对模型进行评估和优化。常用的评估指标包括准确率（accuracy）、精确率（precision）、召回率（recall）和F1分数（F1 score）。

对应的代码如下：

# 对验证集数据进行转换
X_val_scaled = preprocessor.transform(X_val)

# 预测验证集
val_predictions = model.predict(X_val_scaled)

# 模型评估
accuracy = accuracy_score(y_val, val_predictions)
precision = precision_score(y_val, val_predictions)
recall = recall_score(y_val, val_predictions)
f1 = f1_score(y_val, val_predictions)
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)

# 预测测试集
predictions = model.predict(X_test_scaled)

# 将预测结果添加到测试集
test_data['Survived'] = predictions

# 保存预测结果为CSV文件
test_data.to_csv('predictions.csv', index=False)

以上代码对转换后的验证集进行预测，并计算模型在验证集上的性能指标。然后，使用训练好的模型对测试集进行预测，并将预测结果添加到测试集中。最后，将包含预测结果的测试集保存为CSV文件。

5. 数据可视化

5.1 幸存者与非幸存者的人数比较

此部分先统计测试集中存活和非存活乘客的数量，并通过条形图和饼图进行可视化展示。然后，根据测试集中存活乘客的PassengerId创建条形图，用于显示幸存乘客的分布情况。

下面是幸存者与非幸存者人数比较的代码示例：

# 统计存活和非存活乘客的数量
survived_count = test_data['Survived'].value_counts()

# 创建条形图统计存活和非存活的数量
plt.figure(figsize=(6, 4))
survived_count.plot(kind='bar', color=['lightblue', 'lightgreen'])
plt.xlabel('Survived')
plt.ylabel('Count')
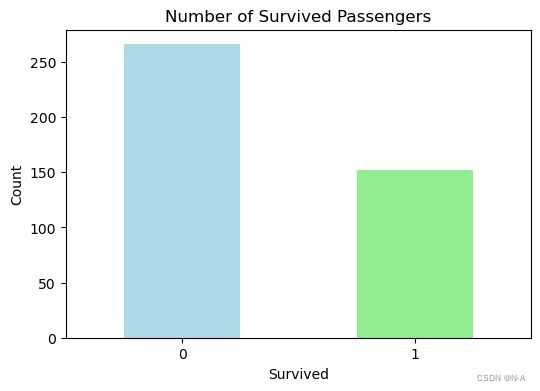
plt.title('Number of Survived Passengers')
plt.xticks(rotation=0)
plt.show()

对应的结果如下图所示：

​ 图5-1 存活和非存活的数量柱状图

# 创建饼图统计存活与非存活率
plt.figure(figsize=(4, 4))
plt.pie(survived_count, labels=survived_count.index, autopct='%1.1f%%', startangle=90, colors=['lightblue', 'lightgreen'])
plt.title('Survival Rate of Passengers')
plt.axis('equal')
plt.show()

对应的结果如下图所示：

​ 图5-2 存活和非存活比率饼状图

# 使用训练集数据来判断乘客的幸存情况
train_data['Survived'] = train_data['Survived'].map({0: 'No', 1: 'Yes'})

# 根据测试集中的PassengerId进行可视化
survived_passengers = test_data[test_data['Survived'] == 1]
survived_passenger_ids = survived_passengers['PassengerId']

# 创建幸存乘客的条形图
plt.figure(figsize=(12, 6))
plt.bar(survived_passenger_ids, [1] * len(survived_passenger_ids), color='green')
plt.xlabel('PassengerId')
plt.ylabel('Survived')
plt.title('Survival of Passengers')
plt.xticks(rotation=90)
plt.show()

对应的结果如下图所示：

​ 图5-3 幸存乘客的条形图

最后的幸存乘客条形图，使用plt.figure(figsize=(12, 6))创建一个图形窗口，设置图形的大小。使用plt.bar(survived_passenger_ids, [1] * len(survived_passenger_ids), color=‘green’)创建条形图，将存活乘客的PassengerId作为x轴，取值为1的列表作为y轴，条形的颜色为绿色。即对应的乘客幸存则会有对应的绿色柱条。

5.2 不同特征与生存率的关系可视化

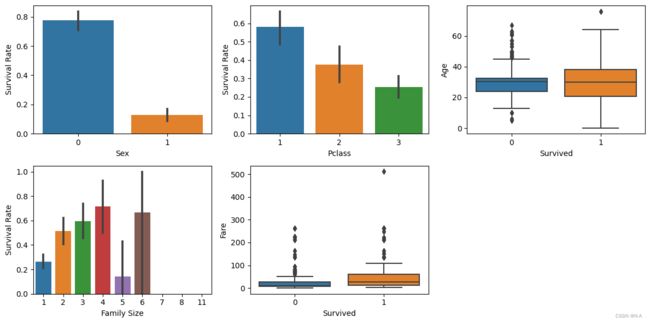
侧部分分析不同特征与生存率的关系的可视化。通过条形图和箱线图展示了不同特征与生存率之间的关系，帮助分析各个特征对乘客生存率的影响。

下面是不同特征与生存率关系可视化的代码示例：

# 数据可视化
# 不同特征与生存率的关系可视化
plt.figure(figsize=(12, 6))

# 性别与生存率的关系
plt.subplot(2, 3, 1)
sns.barplot(x='Sex', y='Survived', data=test_data)
plt.xlabel('Sex')
plt.ylabel('Survival Rate')

# 船舱等级与生存率的关系
plt.subplot(2, 3, 2)
sns.barplot(x='Pclass', y='Survived', data=test_data)
plt.xlabel('Pclass')
plt.ylabel('Survival Rate')

# 年龄与生存率的关系
plt.subplot(2, 3, 3)
sns.boxplot(x='Survived', y='Age', data=test_data)
plt.xlabel('Survived')
plt.ylabel('Age')

# 家庭大小与生存率的关系
plt.subplot(2, 3, 4)
sns.barplot(x='FamilySize', y='Survived', data=test_data)
plt.xlabel('Family Size')
plt.ylabel('Survival Rate')

# 票价与生存率的关系
plt.subplot(2, 3, 5)
sns.boxplot(x='Survived', y='Fare', data=test_data)
plt.xlabel('Survived')
plt.ylabel('Fare')
plt.tight_layout()
plt.show()

对应的结果如下图所示：

​ 图5-4 不同特征与生存率的关系可视化

6. 数据分析结论与建议

6.1 结论总结

本章将对泰坦尼克号数据集进行数据分析，并根据分析结果提出相关建议。首先，我们将探索不同特征与乘客生存率之间的关系，然后基于分析结果提出预测模型的建议。

6.2 特征与生存率的关系分析

根据数据摘要和统计分析，我们可以得出以下结论：

船舱等级（Pclass）与生存率存在相关性，一等舱的乘客生存率较高，而三等舱的乘客生存率较低。

性别（Sex）与生存率强相关，女性的生存率较高，而男性的生存率较低。

年龄（Age）与生存率相关性较弱，不同年龄段的乘客生存率相差不大。

同辈亲属数量（SibSp）和不同辈亲属数量（Parch）与生存率之间的关系较复杂，没有明显的线性相关性。

票价（Fare）与生存率存在一定的相关性，票价较高的乘客生存率较高。

家庭大小（FamilySize）与生存率之间的关系也较为复杂，家庭成员数量适中的乘客生存率较高。

6.3 基于分析结果的建议

考虑船舱等级（Pclass）作为一个重要特征，可以将其纳入预测模型中。一等舱的乘客生存率较高，可能与其在紧急情况下获得更多的救援资源有关。

性别（Sex）是另一个重要的特征，女性的生存率较高。因此，在预测模型中，应考虑性别作为一个关键特征。

年龄（Age）虽然与生存率相关性较弱，但可以考虑将其纳入预测模型中，以探索可能的年龄相关模式。

票价（Fare）作为一个与生存率相关的特征，可以用作预测模型的输入。较高票价的乘客可能在紧急情况下享有更好的救援资源。

家庭大小（FamilySize）也可以作为一个特征，考虑家庭成员数量对乘客生存率的影响。然而，需要注意家庭大小与生存率之间的复杂关系，以避免过度解读数据。

7. 总结

7.1 研究总结

本文对泰坦尼克号生存情况数据集进行了详细的数据分析和预测。首先，对数据进行了探索性分析，包括数据的基本统计特征和缺失值的处理。然后，进行了特征工程，对数据进行了填充、转换和创建新特征。接着，选择了随机森林算法进行模型训练和预测，并评估了模型的性能。通过可视化分析，深入了解了不同特征与生存率之间的关系。最后，总结了分析结果并提出了相应的建议。

7.2 局限性和进一步研究的方向

通过本次分析，我们对泰坦尼克号生存情况数据集有了更深入的认识，并获得了对乘客生存情况的预测模型。这些分析和结果可以为制定救援计划、资源分配和决策支持提供有价值的参考。同时，也展示了数据分析在解决实际问题中的重要性和应用价值。在未来的研究和实践中，可以进一步改进模型、探索更多特征和算法，并将数据分析应用于更广泛的领域和实际场景中，为决策和问题解决提供更多洞见和支持。