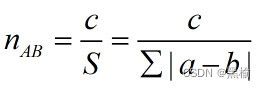时序与空间结构

移位距离假设

(A，B)---m*n*k---(1,0)(0,1)

用神经网络分类A和B，把参与分类的A和B中的数字看作是组成A和B的粒子，分类的过程就是让A和B中的粒子互相交换位置，寻找最短移位路径的过程。而熵H与最短移位距离S成正比，迭代次数n与S成反比。

移位规则汇总

移位距离就是等位点数值差的绝对值的和S=Σ|a-b|，如果训练集有多张图片取平均值，如果是多分类问题则移位距离为所有两两组合移位距离的和。

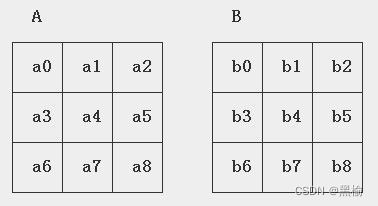
如对一组3*3的矩阵

S=s0+s1+，…，+s8=|a0-b0|+|a1-b1|+,…,+|a8-b8|

如果是3分类问题，就应该实现3个形态之间的两两分类，也就是要完成3对等位点之间的差。

因此移位距离

S=Sab+Sac+Sbc=

|a0-b0|+|a1-b1|+|a2-b2|+|a3-b3|+

|a0-c0|+|a1-c1|+|a2-c2|+|a3-c3|+

|b0-c0|+|b1-c1|+|b2-c2|+|b3-c3|

这次继续验算这一假设，所用训练集为mnist的0，1，2，3，4的第一张图片，做一个3分类网络，来验证迭代次数和移位距离的关系

( A, B, C )---m*n*k---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

首先用间隔取点的办法把图片化成9*9，网络结构为

( A, B, C )---81*30*3---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

得到数据

9*9	δ	0.01	0.001	9.00E-04	8.00E-04	7.00E-04	S平均
1*3*4	迭代次数n	2248.477	15564.5	17165.27	19037.75	21613.02	52
2*3*4	迭代次数n	2058.874	14731.81	16207.58	18052.38	20439.4	90
1*2*4	迭代次数n	2041.126	14661.05	16110.55	17955.89	20321.21	82
0*3*4	迭代次数n	1981.261	14410.76	15882.11	17717.5	20086.51	88
0*1*3	迭代次数n	2011.693	14226.95	15649.56	17446.29	19849.48	82
0*1*4	迭代次数n	1961.472	14246.09	15699.46	17460.94	19833.61	82
1*2*3	迭代次数n	2005.533	14162.56	15554.51	17324.29	19712.56	86
0*1*2	迭代次数n	1861.744	13256	14571.18	16156.77	18359.36	70
0*2*3	迭代次数n	1774.553	12471.54	13759.03	15339.65	17300.2	82
0*2*4	迭代次数n	1772.955	12289.27	13521.05	15107.41	17049.99	90

如1*2*3的意思为

( 1, 2, 3 )---81*30*3---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

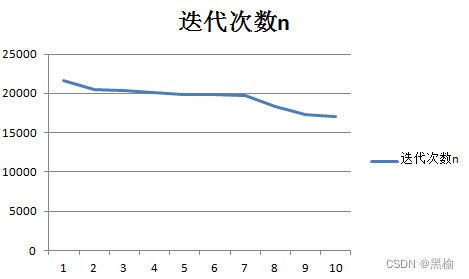
将收敛误差为7e-4的迭代次数画成图

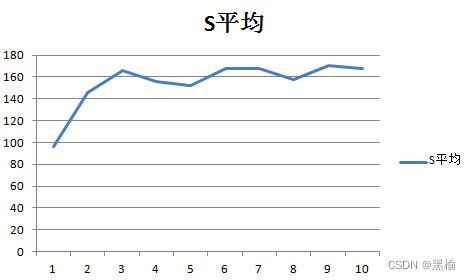
将移位距离S画成图

尽管S曲线的波动较大，但S和n之间的反比关系仍然是清晰的。

再一次验算将图片化成11*11，网络结构为

( A, B, C )---121*30*3---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

得到数据为

	δ	0.01	0.001	9.00E-04	8.00E-04	7.00E-04	S平均
1*3*4	迭代次数n	1879.935	13735.02	15173.34	16891.76	19181.42	96
0*3*4	迭代次数n	1789.307	13405.12	14714.66	16475.77	18591.92	146
2*3*4	迭代次数n	1725.171	13303.93	14550.28	16220.5	18409.24	166
0*1*4	迭代次数n	1740.226	12824.57	14240.37	15887.85	18000.18	156
0*1*3	迭代次数n	1738.045	12944.04	14307.66	15907.33	17982.46	152
1*2*4	迭代次数n	1722.628	12867.81	14121.82	15764.27	17889.45	168
1*2*3	迭代次数n	1692.377	12826.67	14120.54	15755.62	17850.13	168
0*1*2	迭代次数n	1565.814	11809.94	12998.81	14557.29	16571.86	158
0*2*4	迭代次数n	1560.085	11508.12	12676.15	14163.69	16176.46	170
0*2*3	迭代次数n	1547.613	11531.02	12737.23	14278.24	16147.87	168

画出s曲线和n曲线

可见s和n之间的反比关系很明显，s增加而n减小。

所以综合前面的实验，对两张图片的二分类问题s和n之间保持了一种很严格的反比关系。而对3张图片的二分类问题和3张图片的3分类问题s和n之间确只能做到近似相符,为什么会是这样？

( A，B )---m*n*k---(1,0)(0,1)

( 粒子，环境 )---m*n*k---(1,0)(0,1)

这件事或许可以做如下猜测，对于一个二分类网络，可以将分类的两个对象理解为粒子和环境，粒子处在环境中，而环境中只有这一个粒子。在这个物理环境中是没有时间的。因此这个粒子或者是静止或者做匀速直线运动，这个粒子的过去和未来没有任何区别，这等价于时间是静止的。这个粒子可以随意的穿梭到过去和未来。

或者理解为粒子在环境中，则粒子在任意时刻相对环境都有一个相对距离为0的状态，粒子和环境的相对距离为0，而t=s/v则无论粒子和环境之间如何相互作用，这种力的作用过程都将是瞬时的，耗时为0.所以无论用哪种方式理解在仅有1个粒子的环境中，没有时间变量。A和B是瞬时作用。

( A B，C )---m*n*k---(1,0)(0,1)

( 粒子A  粒子B，环境C )---m*n*k---(1,0)(0,1)

因此对3张图片的二分类问题，可以理解为是粒子A和粒子B与环境C二分类，这时在环境C中存在两个粒子，这时粒子A和B的运动的同时性就是相对的。这也就意味着这个环境中出现了一个新的变量,t时间。A和B运动的先后出现了时序问题。

( A, B, C )---m*n*k---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

( 粒子A, 粒子B, 环境C )---m*n*k---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

同样对于3分类问题，如果假设粒子和环境的作用是瞬时的，那粒子和粒子之间的相互作用也总有先后问题，同样会导致时序t的产生。

所以之所以在3张图片的二分类问题和3张图片的三分类问题中会有对称导致的不规则的结构耦合效应，是因为相对两张图片的二分类问题出现了一个新的物理量时序t。