顺序表的插入，删除，修改和查找（详细解析）

目录

一.顺序表的初始化----静态分配

二.顺序表的初始化----动态分配

三.顺序表的插入

1.插入操作

2.插入操作的时间复杂度

三.顺序表的删除操作

1.顺序表的删除

 2.删除操作的时间复杂度

四.顺序表的查找

1.按位查找操作：查找第i位置的元素

2.按位查找操作的时间复杂度：O(1)

3.按值查找操作

4.按值查找的时间复杂度

---

一.顺序表的初始化----静态分配

#include
#define MaxSize 10
typedef struct{
    int data[MaxSize];
    int length;
}SqList;

void InitList(SqList &L)
{
    for(int i=0;i

不能写为

#include
#define MaxSize 10
typedef struct{
    int data[MaxSize];
    int length;
}SqList;

void InitList(SqList &L)
{
    L.length=0;
}

int main()
{
    SqList L;
    InitList(L);
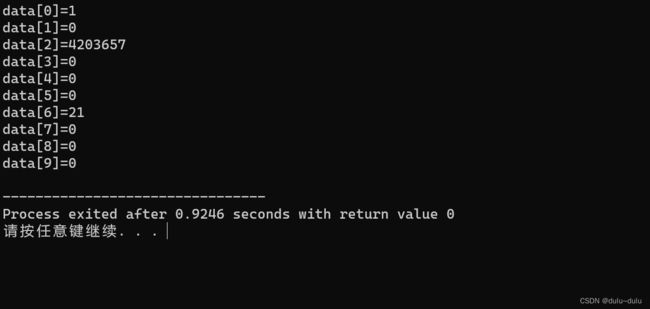
    for(int i=0;i

结果为

 其中有两个错误

1.未初始化数据

因为在初始化时没有设置数据元素的默认值，内存中会出现上述“4203657”，“21”这类遗留脏数据

2.i

上述代码中的i操作其实是不合理的，应该访问到顺序表的最后一个元素截止，不应该访问大于数据表长度的元素，即i

若L.length>MaxSize会报错，若将MaxSize设的稍微大些，有可能造成内存的浪费，所以最好的解决方式就是动态内存分配

二.顺序表的初始化----动态分配

#include
#include

#define InitSize 10
typedef struct{
    int *data;//指示动态分配数组的指针:L.data=(int *)malloc(InitSize*sizeof(int));
    int MaxSize;//顺序表的最大容量
    int length;//顺序表的当前长度

}SeqList;

void InitList(SeqList &L)
{
//申请一段连续的存储空间
    L.data=(int*)malloc(InitSize*sizeof(int));
    L.length=0;
    L.MaxSize=InitSize;

}

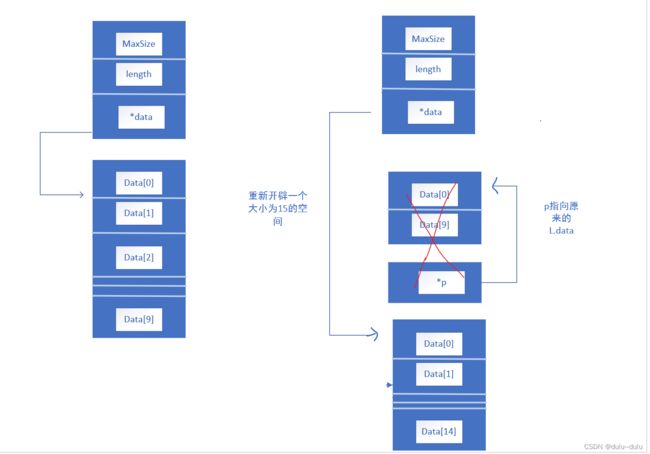
//开辟一段新的空间
void IncreaseSize(SeqList &L,int len)
{
    int *p=L.data;
    L.data=(int *)malloc((L.MaxSize+len)*sizeof(int));
    for(int i=0;i

free函数会将*p（p指针）所指向的整块存储空间释放，归还给系统，同时p是一个局部变量，当这个函数结束后，p这个变量的存储空间也将被释放 

三.顺序表的插入

1.插入操作

#define MaxSize 10    //定义最大长度
typedef struct
{
    ElemType data[MaxSize];
    int length;//顺序表当前长度
}SqList;//顺序表类型定义


void ListInsert(SqList &L,int i,int e)
{
    for(int j=L.length;j>=i;j--)//将第i个元素及之后的元素后移
        L.data[j]=L.data[j-1];
    L.data[i-1]=e;
//将需要插入的元素赋值e,因为数组从L.data[0]开始,所以这里第i个元素是[i-1]表示的
    L.length++;
}

int main()
{
    SqList L;//声明一个顺序表
    InitList(L);
    ListInsert(L,3,3);//在三个位置插入数据元素3


}

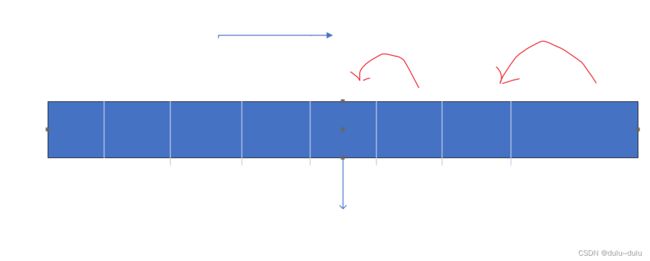
 如下图所示，表示ListInsert(L,3,3)

 若执行ListInsert(L,9,3),则会产生如下现象

 中间的值data[6],data[7]空了，而在顺序表中元素应该相邻存放，说明这段代码不够健壮，应该做如下调整

bool ListInsert(SqList &L,int i,int e)
{
    if(i<1||i>L.length+1)//判断i的范围是否有效
        return false;
    if(L.length>=MaxSize)//判断当前存储空间是否已满
        return false;
    for(int j=L.length;j>=i;j--)
    {
        L.data[j]=L.data[j-1];
    }
    L.data[i-1]=e;
    L.length++;
    return true;
}

2.插入操作的时间复杂度

最好情况:新元素插入到表尾，不需要移动元素
i= n+1，循环0次;最好时间复杂度=O(1)；

最坏情况:新元素插入到表头，需要将原有的n个元素全都向后移动

i= 1，循环 n 次;最坏时间复杂度O(n)；

平均情况：假设新元素插入到任何一个位置的概率相同，即i= 1,2,3,...,length+1 的概率都是 p=1/n+1，i= 1，循环 n 次;i=2 ，循环 n-1，i+3，循环n-2次，.....i=n+1时，循环0次
平均循环次数 =np +(n-1)p +(n-2)p + 1*p=(n(n+1)/2)*(1/n+1)=n/2

三.顺序表的删除操作

1.顺序表的删除

bool ListDelete(SqList &L,int i,int &e)
{
    if(i<1||i>L.length)
        return false;
    e=L.data[i-1];
    for(int j=i;j

插入

for(int j=L.length;j>=i;j--)//从后到前依次往后挪

 

删除

for(int j=i;j

 

 2.删除操作的时间复杂度

最好情况:删除表尾元素，不需要移动其他元素
i= n，循环 0 次;最好时间复杂度 = O(1)

最坏情况:删除表头元素，需要将后续的 n-1 个元素全都向前移动

i= 1，循环 n-1 次;最坏时间复杂度 = O(n);

平均情况:假设删除任何一个元素的概率相同，即i= 1,2,3,...,length 的概率都是 p=1/n

平均循环次数 =(n-1)p +(n-2)p + 1*p=(n(n-1)/2)*(1/n)=n-1/2

四.顺序表的查找

1.按位查找操作：查找第i位置的元素

#define InitSize 10    //顺序表的初始长度
#include
#include
typedef struct
{
    int *data;    //指示动态分配数组的指针
    int MaxSize;
    int length;
}SeqList;

void InitList(SeqList &L)
{
    L.data=(int *)malloc(InitSize*sizeof(int));
    L.length=10;
    L.MaxSize=InitSize;
}

int GetElem(SeqList L,int i)
{
    return L.data[i-1];
}

int main()
{
	SeqList L;
	InitList(L); 
	for(int i=0;i

2.按位查找操作的时间复杂度：O(1)

3.按值查找操作

#define InitSize 10
#include
#include

typedef struct{
    int *data;
    int MaxSize;
    int length;
} SeqList;

void InitList(SeqList &L)
{
    L.data = (int *)malloc(InitSize * sizeof(int));
    L.length = 10;
    L.MaxSize = InitSize;
}

// 在顺序表L中查找第一个元素值等于e的元素，并返回其位序
int LocateElem(SeqList L, int e)
{
    for(int i=0; i

4.按值查找的时间复杂度

最好情况:目标元素在表头
循环1次;最好时间复杂度 = O(1)

最坏情况:目标元素在表尾

循环 n 次;最坏时间复杂度 = O(n);
平均情况:假设目标元素出现在任何一个位置的概率相同，都是1/n
目标元素在第1位，循环1次;在第2位，循环2次;在第 n位，循环 n 次...... ;
平均循环次数 =1*1/n +1/n*2 +1/n*3 + =(n(n+1)/2)*(1/n)=n+1/2