堆排序问题（TOP-K问题）

目录

1.堆的概念及结构

2.堆的创建

1.框架基本

 2.堆的插入和删除

3.其余函数的实现

3.堆排序问题

1.如何利用数组直接建堆，进行排序

4.TOP-K问题

5.总结

---

---

1.堆的概念及结构

如果有一个关键码的集合K ={K0 ,K1,K2,K3…，Kn-1,Kn }，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足：Kik2*i+1 且Ki>K2*i+2)则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：

    堆中某个节点的值总是不大于或不小于其父节点的值；

    堆总是一棵完全二叉树。

例如：

2.堆的创建

1.框架基本

本次代码建立一个小堆（即每一个父亲节点小于孩子节点）

#pragma once
#include
#include
#include
#include
#include
typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;
	size_t size;//表示数组的下标
	size_t capacity;//表示容量的大小
}HP;

void Swap(HPDataType* pa, HPDataType* pb);//交换两个数据的位置
void HeapInit(HP* php);//堆初始化
void HeapDestroy(HP* php);//堆的销毁
void HeapPrint(HP* php);//打印数组
void HeapPush(HP* php, HPDataType x);//插入数据
void HeapPop(HP* php);//删除数据
bool HeapEmpty(HP* php);//判空
size_t HeapSize(HP* php);//判断堆中元素的个数
HPDataType HeapTop(HP* php);//返回堆中第一个元素

 2.堆的插入和删除

插入

void Swap(HPDataType* pa, HPDataType* pb)；
void AdjustUp(HPDataType* a, size_t child)；
void AdjustDown(HPDataType* a, size_t size, size_t root)；
void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);
		}

		php->a = tmp;
		php->capacity = newCapacity;
	}
    php->a[php->size] = x;
	++php->size;

	AdjustUp(php->a, php->size - 1);//插入一个元素后，进行向上条整
}
void Swap(HPDataType* pa, HPDataType* pb)
{
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
void AdjustUp(HPDataType* a, size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)//向上调整，直到根节点
	{
		if (a[child] < a[parent])//此次建立小堆，若parent节点>child>节点，即交换
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

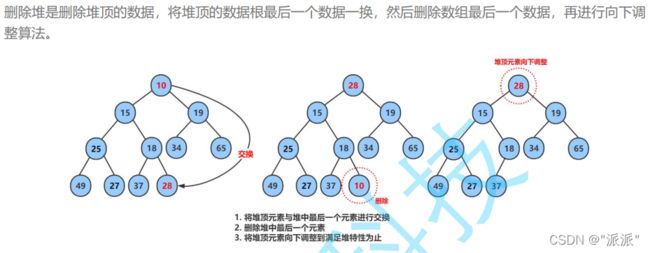
删除 

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);//交换第一个节点与最后一个节点
	--php->size;//把交换后，处于最后位置的节点删除
	AdjustDown(php->a, php->size, 0);//除第一个节点以外，符合堆的性质，采用向下调整的方法
}
void AdjustDown(HPDataType* a, size_t size, size_t root)
{
	size_t child= root * 2 + 1;//先找到左孩子节点
	size_t parent = root;
	while (child a[child])//如果父亲节点大于最小的那个孩子节点，即交换
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

3.其余函数的实现

void HeapInit(HP* php)
{
	php->capacity = php->size = 0;
	php->a = NULL;
}
void HeapDestroy(HP* php)
{
	php->capacity = php->size = 0;
	free(php->a);
	php->a = NULL;
}
void HeapPrint(HP* php)
{
	assert(php);
	for (size_t i = 0; i < php->size; ++i)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}
bool HeapEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}

size_t HeapSize(HP* php)
{
	assert(php);

	return php->size;
}

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	return php->a[0];
}

3.堆排序问题

1.如何利用数组直接建堆，进行排序

int main()
{
	int a[] = { 4, 2, 7, 8, 5, 1, 0, 6 };
	HeapSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	return 0;
}

1.采用向上调整方法（即上面堆的插入算法）

void HeapSort(int* a, int n)
{
   for(int i=1;i 0)//建堆之后进行排序排序
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);//把第一个元素换到最后，保持其位置不变，再进行向下调整
		--end;
	}
}

时间复杂度分析 ：

节点移动的总次数为：2^1*1+2^2*2+2^3*3+.......+2^(h-1)*h

建堆的时间复杂度为：O(N*logN)

2.采用向下调整算法

向下调整需要确保节点已经是堆，所以可以先从最后面的父亲节点开始，确保其孩子节点与其点满足堆的性质，再往上找父亲节点，再确保其孩子节点与其点满足堆的性质，再进行反复操作，直到根节点。

void HeapSort(int* a, int n)
{
	
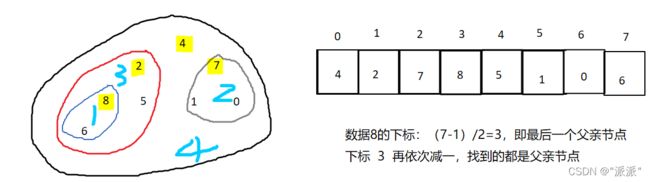
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)//建堆
	{
		AdjustDown(a, n, i);
	}
	size_t end = n - 1;//最后一个数据的下标
	while (end > 0)    //建堆之后进行排序排序，此次建的是小堆
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);//把第一个元素(最小的元素)与最后那个元素交换，再进行向下调整
         --end;               //再把次小的元素与倒数第二个元素交换，(此时最后那个元素不在堆的 
                              //范围内，循环操作)
	}
}

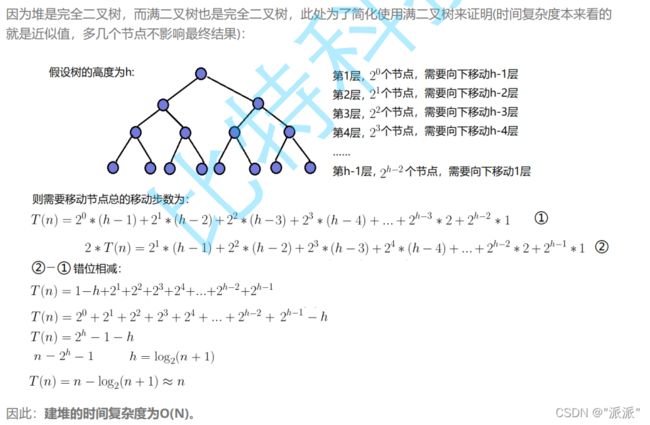
时间复杂度分析：

 结论：建堆最好使用向下建堆的方法

4.TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。 比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

1. 用数据集合中前K个元素来建堆 前k个最大的元素，则建小堆 前k个最小的元素，则建大堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素将剩余N-K个元素依次与堆      顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kminHeap = (int*)malloc(sizeof(int)*k);
	assert(kminHeap);

	for (int i = 0; i < k; ++i)
	{
		kminHeap[i] = a[i];
	}

	// 建小堆
	for (int j = (k - 1 - 1) / 2; j >= 0; --j)
	{
		AdjustDown(kminHeap, k, j);
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，若比堆顶元素大，则进行替换
	for (int i = k; i < n; ++i)
	{
		if (a[i] > kminHeap[0])
		{
			kminHeap[0] = a[i];
			AdjustDown(kminHeap, k, 0);//替换后，在进行向下调整
		}
	}

	for (int j = 0; j < k; ++j)
	{
		printf("%d ", kminHeap[j]);
	}
	printf("\n");
	free(kminHeap);
}
void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int)*n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
//随便给出比100000大的数
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 1000000 + 5;
	a[2305] = 1000000 + 6;
	a[99] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[0] = 1000000 + 1000;
	PrintTopK(a, n, 10);
}
int main()
{
	TestTopk();
	return 0;
}
结果：
1000001 1000002 1000003 1000005 1000009 1000006 1000004 1000007 1000008 1001000

C:\Users\if\Desktop\world\Project2\Debug\Project2.exe (进程 31404)已退出，代码为 0。
按任意键关闭此窗口. . .

5.总结

要对每一个细节了解清楚，举例进行分析，循序渐进。