最短路径的四种算法

最短路径四种算法

1	2	3	4
Floyd	Dijkstra	Bellman-Ford	队列优化的Bellman-Ford

一，只有四行的算法——Floyd-Warshall

假设求顶点$Vi$到$Vj$的最短路径。弗洛伊德算法依次找从$Vi$到$Vj$，中间经过结点序号不大于$0$的最短路径，不大于$1$的最短路径，…直到中间顶点序号不大于$n-1$的最短路径，从中选取最小值，即为$Vi$到$Vj$的最短路径。

算法具体描述
若从$Vi$到$Vj$有弧，则从$Vi$到$Vj$存在一条长度为弧上权值$（arcs[i][j]）$的路径，该路径不一定是最短路径，尚需进行$n$次试探。

首先考虑从$Vi$到$Vj$经过中间顶点$V0$的路径$（Vi，V0，Vj）$是否存在，也就是判断弧$（Vi，V0）$和$（V0，Vj）$是否存在。若存在，则比较$（Vi，Vj）$和$（Vi，V0，Vj）$的路径长度取较短的为从$Vi$到$Vj$的中间顶点序号不大于0的最短路径。

在此路径上再增加一个顶点$V1$，也就是说，如果$（Vi，\dots V1）$和$（V1，\dots Vj）$分别是当前找到的中间顶点序号不大于$0$的最短路径，那么，$（Vi，\dots V1，\dots Vj）$就有可能是从$Vi$到$Vj$的中间顶点序号不大于$1$的最短路径。将它和已经得到的从$Vi$到$Vj$中间顶点序号不大于$0$的最短路径相比较，从中选出最短的作为从$Vi$到$Vj$中间顶点序号不大于$1$的最短路径。 然后，再增加一个顶点$V2$继续进行这个试探过程。

一般情况下，若$（Vi，\dots Vk）$和$（Vk，\dots Vj）$分别是从$Vi$到$Vk$和从$Vk$到$Vj$的中间顶点序号不大于k-1的最短路径，则将$（Vi，\dots ，Vk，\dots Vj）$和已经得到的从$Vi$到$Vj$的中间顶点序号不大于$k-1$的最短路径相比较，其长度最短者即为从$Vi$到$Vj$的中间顶点序号不大于$k$的最短路径。

经过$n$次比较之后，最后求得的便是从$Vi$到$Vj$的最短路径。
假设有下面的一些路:

起始点	终止点	距离
1	2	2
1	3	6
1	4	4
2	3	3
3	1	7
3	4	1
4	1	5
4	3	12

现定义一个$4$阶方阵序列:
现初始化方阵为：

\	1	2	3	4
1	0	$\infty$	$\infty$	$\infty$
2	$\infty$	0	$\infty$	$\infty$
3	$\infty$	$\infty$	0	$\infty$
4	$\infty$	$\infty$	$\infty$	0

因为$1$到$1$没有距离所以初始化为$0$,之后把点与点之间的关系放入矩阵

\	1	2	3	4
1	0	2	6	4
2	$\infty$	0	3	$\infty$
3	7	$\infty$	0	1
4	5	$\infty$	12	0

从图中$4\to 3$的直观路程为12但还可以$4\to 1\to 3$这样路程就缩短了$1$为$11$
通过这些例子我们可以发现每一个点都有可能从这种方式使得另外两个点的距离变短；

整个算法过程其实很简单

for(int k=1;k<=n;k++)// i,j,k分别表示三个点
   for(int i=0;i<=n;i++)//遍历一遍得出最短路径
       for(int j=0;j<=n;j++)
          e[i][j]=min(e[i][j],e[i][k]+e[k][j]);//e[][]存储两点之间的距离

优点：容易理解，可以算出两个节点之间最短距离的算法，程序容易写，可以处理带有负权边的图（但不能有负权回路）并且均摊到每一点对上，在所有算法中还是属于较优的

缺点：复杂度达到三次方，不适合计算大量数据

二，Dijkstra 算法

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。
基本思想

通过Dijkstra计算图G中的最短路径时，需要指定起点$s$(即从顶点$s$开始计算)。

此外，引进两个集合$S$和$U$。$S$的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，$S$中只有起点$s$；$U$中是除$s$之外的顶点，并且$U$中顶点的路径是"起点$s$到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到$S$中；接着，更新$U$中的顶点和顶点对应的路径。 然后，再从$U$中找出路径最短的顶点，并将其加入到$S$中；接着，更新$U$中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

操作步骤

(1) 初始时，$S$只包含起点$s$；$U$包含除$s$外的其他顶点，且$U$中顶点的距离为"起$点s$到该顶点的距离"[例如，$U$中顶点$v$的距离为$(s,v)$的长度，然后$s$和$v$不相邻，则$v$的距离为$\infty$ 。

(2) 从$U$中选出"距离最短的顶点$k$"，并将顶点$k$加入到$S$中；同时，从$U$中移除顶点$k$。

(3) 更新$U$中各个顶点到起点$s$的距离。之所以更新$U$中顶点的距离，是由于上一步中确定了$k$是求出最短路径的顶点，从而可以利用$k$来更新其它顶点的距离；例如，$(s,v)$的距离可能大于$(s,k)+(k,v)$的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

迪杰斯特拉算法图解

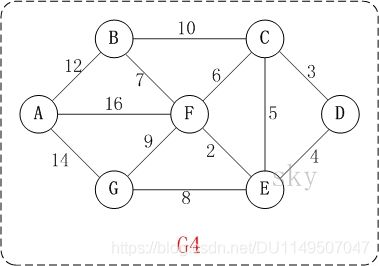
以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点$D$为起点)。

初始状态：$S$是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点$D$加入到$S$中。
此时，$S=｛D(0)｝$
$U=｛A(\infty ),B(\infty ),C(3),E(4),F(\infty ),G(\infty )｝$
注:C(3)表示C到起点D的距离是3。

第2步：将顶点$C$加入到$S$中。
上一步操作之后，$U$中顶点$C$到起点$D$的距离最短；因此，将$C$加入到$S$中，同时更新$U$中顶点的距离。以顶点$F$为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为$9=(F,C)+(C,D)。$
此时，
$S=｛D(0),C(3)｝,$
$U=｛A(\infty ),B(23),E(4),F(9),G(\infty )｝$

第3步：将顶点$E$加入到$S$中。
上一步操作之后，$U$中顶点$E$到起点$D$的距离最短；因此，将$E$加入到$S$中，同时更新$U$中顶点的距离。还是以顶点$F$为例，之前$F$到$D$的距离为$9$；但是将$E$加入到$S$之后，$F$到$D$的距离为$6=(F,E)+(E,D)$。
此时，$S=｛D(0),C(3),E(4)｝$
$U=｛A(\infty ),B(23),F(6),G(12)｝$

第4步：将顶点F加入到S中。
此时，$S=｛D(0),C(3),E(4),F(6)｝$
$U=｛A(22),B(13),G(12)｝。$

第5步：将顶点G加入到S中。
此时，$S=｛D(0),C(3),E(4),F(6),G(12)｝,U=｛A(22),B(13)｝$。

第6步：将顶点B加入到S中。
此时，$S=｛D(0),C(3),E(4),F(6),G(12),B(13)｝$
$U=A(22)$。

第7步：将顶点A加入到S中。
此时，
$S=｛D(0),C(3),E(4),F(6),G(12),B(13),A(22)｝$。

此时，起点D到各个顶点的最短距离就计算出来了：$A(22)B(13)C(3)D(0)E(4)F(6)G(12)$

迪杰斯特拉算法核心语句

int n;//表示点数
int book[maxx]//进行标记
int dis[maxx]//可以称作最短路程的估计值
#define inf 0x3f3f3f3f
void dijkstra()
{
    for(int i=1;i<=n;i++)
        dis[i]=e[1][i];//这里是1到各个顶点的距离
    memset(book,0,sizeof(book));
    book[1]=1;
   for(int i=1;i<=n-1;i++)
   {
       min=inf;
       for(int j=1;j<=n;j++)
       {
           if(book[j]==0&&dis[j]<min)
           {
               min=dis[j];
               u=j;
           }
       }
       book[u]=1;
       for(int v=1;v<=n;v++)
       {
           if(e[u][v]<inf)
           {
               if(dis[v]>dis[u]+e[u][v])
                dis[v]=dis[u]+e[u][v];
           }
       }
   }
}

优点:$O(N\ast N)$,加堆优化:$O(N\ast logN)$

缺点: 在单源最短路径问题的某些实例中，可能存在权为负的边。
如果图$G＝（V，E）$不包含从源$s$可达的负权回路，
则对所有$v\in V$，最短路径的权定义$d(s,v)$依然正确，
即使它是一个负值也是如此。但如果存在一从$s$可达的负回路，
最短路径的权的定义就不能成立。$S$到该回路上的结点就不存在最短路径。
当有向图中出现负权时，则Dijkstra算法失效。当不存在源$s$可达的负回路时，
我们可用Bellman-Ford算法实现。

三，Bellman-Ford算法

Dijkstra算法虽好但是不能解决负权边，当不存在负回路时，我们可用Bellman-Ford算法实现。

介绍编辑

Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权，在没有负权回路（回路的权值和为负，即便有负权的边）存在时，也可以采用Bellman - Ford算法正确求出最短路径。

Bellman-Ford算法能在更普遍的情况下（存在负权边）解决单源点最短路径问题。对于给定的带权（有向或无向）图 G=(V,E), 其源点为s，加权函数 w是 边集 E 的映射。对图G运行Bellman - Ford算法的结果是一个布尔值，表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路，算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。

适用条件编辑

1.单源最短路径(从源点s到其它所有顶点$n$);

2.有向图&无向图(无向图可以看作$(u,n),(n,u)$同属于边集E的有向图);

3.边权可正可负(如有负权回路输出错误提示);

4.差分约束系统;

算法描述编辑

1,.初始化：将除源点外的所有顶点的最短距离估计值

$d[n]\to +\infty$, $d[s]\to 0$;

2.迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行$|n|-1$次）

3.检验负权回路：判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回$false$，表明问题无解；否则算法返回$true$，并且从源点可达的顶点$v$的最短距离保存在 $d[n]$中。
描述性证明编辑首先指出，图的任意一条最短路径既不能包含负权回路，也不会包含正权回路，因此它最多包含$|n|-1$条边。

其次，从源点$s$可达的所有顶点如果 存在最短路径，则这些最短路径构成一个以$s$为根的最短路径树。Bellman-Ford算法的迭代松弛操作，实际上就是按每个点实际的最短路径[虽然我们还不知道，但它一定存在]的层次，逐层生成这棵最短路径树的过程。

注意，每一次遍历，都可以从前一次遍历的基础上，找到此次遍历的部分点的单源最短路径。如：这是第$i$次遍历，那么，通过数学归纳法，若前面单源最短路径层次为$1（i-1）$的点全部已经得到，而单源最短路径层次为$i$的点，必定可由单源最短路径层次为$i-1$的点集得到，从而在下一次遍历中充当前一次的点集，如此往复迭代，$[n]-1$次后，若无负权回路，则我们已经达到了所需的目的–得到每个点的单源最短路径。[注意：这棵树的每一次更新，可以将其中的某一个子树接到另一个点下]

反之，可证，若存在负权回路，第[v]次遍历一定存在更新，因为负权回路的环中，必定存在一个“断点”，可用数学手段证明。

最后，我们在第$[n]$次更新中若没有新的松弛，则输出结果，若依然存在松弛，则输出$CANT$表示无解。同时，我们还可以通过“断点”找到负权回路。
先看看核心代码长啥样：

从u[]顶点到v[]顶点的权值为w[];
for(int k=1;k<=n-1;k++)
    for(int i=1;i<=m;i++)
    dis[v[i]]=min(dis[v[i]],dis[u[i]]+w[i]);//dis[]数组和dijkstra一样来记录路径
    //上面的一行的意思是看看能否通过u[i]->v[i]（权值为w[i]）这条边,使得起始顶点到v[i]的距离变短

具体如下

bool Bellman_Ford()  
{  
    for(int i = 1; i <= nodenum; ++i) //初始化  
        dis[i] = (i == original ? 0 : MAX);  
    for(int i = 1; i <= nodenum - 1; ++i)  
        for(int j = 1; j <= edgenum; ++j)  
            if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛（顺序一定不能反~）  
            {  
                dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;  
                pre[edge[j].v] = edge[j].u;  
            }  
    bool flag = 1; //判断是否含有负权回路  
    for(int i = 1; i <= edgenum; ++i)  
        if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)  
        {  
            flag = 0;  
            break;  
        }  
        return flag;  
} 

四，Bellman-Ford的队列优化算法

在上面介绍的Bellman-Ford算法中，在每实施一次松弛操作之后，就会有一些顶点已经求得其最短路径，此后，这些顶点的最短路径的值就会一直保持不变，不再受到后续松弛操作的影响，但是每次还要判断是否需要松弛，这里浪费了时间。因此，我们可以考虑每次仅针对最短路径值发生了变化的顶点的所有出边执行松弛操作。这就是Bellman-Ford的队列优化算法。
那么，如何知道当前哪些点的最短路程发生了变化呢？
用一个队列来维护这些点，每次选取队首顶点u，对顶点u的所有出边进行松弛操作。假如有一条u->v的边，如果松弛成功(dist[v] > dist[v] + e[u][v]),则将顶点v放入队尾，需要注意的是，同一个顶点不能同时在队列中出现多次，但是允许一个顶点在出队后再入队。在将顶点u的所有的出边松弛完毕后，就将顶点u出队。接下来不断从队列中取出新的队首顶点进行如上操作，直至队列为空。这就是Bellman-Ford的队列优化算法。下面举一个例子。
新建一个图

//5个顶点，7条边
[1,2,2],
[1,5,10],
[2,3,3],
[2,5,7],
[3,4,4],
[4,5,5],
[5,3,6]]

初始化dist数组和队列。

选取队首顶点1，对顶点1所有的出边就行松弛。顶点2，和5松弛成功，分别将2和5入队。

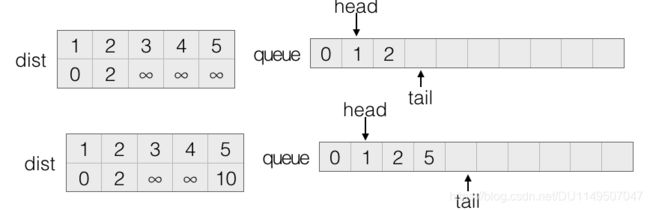
顶点1出队，然后选取队首顶点2进行如上处理。注意2->5这条边松弛成功，但因为5号顶点已经在队列中，所以不进行入队操作。

在对2号顶点处理完毕后，将2号顶点出队，再选取队首5号顶点进行以上处理，知道队列为空，具体步骤就省略了，最后处理的结果如下：

核心代码如下：

inline void spfa(int s)
{

    fill(dis+1,dis+n+1,2147483647);
    memset(vis,false,sizeof(vis));
    dis[s]=0,que[1]=s,vis[s]=true;
    int head=0,tail=1,u;
    while(head

\	Floyd	Dijkstra	Bellman-Ford	队列优化的Bellman-Ford
空间复杂度	$O(N^2)$	$O(M)$	$O(M)$	$O(M)$
时间复杂度	$O(N^3)$	$O((M+N)logN)$	$O(NM)$	最坏也是$O(NM)$
适用情况	稠密图和顶点关系密切	稠密图和顶点关系密切	稀疏图和边关系密切	稀疏图和边关系密切
负权	可以解决负权	不能解决负权	可以解决负权	可以解决负权
有负权边	可以处理	不能处理	可以处理	可以处理
判定是否存在负权回路	不能	不能	可以判定	可以判定

注：从图中可以知道选择最短路径算法时，要根据实际需求和每一种算法的特性，选择合适的算法。
未完待续$\cdot \cdot \cdot \cdot \cdot$