【数据结构与算法——TypeScript】图结构(Graph)
【数据结构与算法——TypeScript】
图结构(Graph)
认识图结构以及特性
什么是图?
- 在计算机程序设计中，图结构 也是一种非常常见的数据结构。
- 但是，图论其实是一个非常大的话题
- 认识一下关于图的一些内容
- 图的抽象数据类型
- 一些算法实现。
- 什么是图?
- 图结构是一种与树结构有些相似的数据结构。
- 图论是数学的一个分支，并且，在数学的概念上，树是图的一种。
- 它以图为研究对象，研究 顶点 和 边 组成的图形的数学理论和方法。
- 主要研究的目的是事物之间的关系，顶点代表事物，边代表两个事物间的关系
- 我们知道树可以用来模拟很多现实的数据结构
- 比如： 家谱/公司组织架构等等
- 那么图长什么样子?
- 或者什么样的数据使用图来模拟更合适呢?
图的现实案例
- 人与人之间的关系网。
- 甚至科学家们在观察人与人之间的关系网时，还发现了六度空间理论。
- 六度空间理论
- 理论上认为世界上任何两个互相不认识的两人。
- 只需要很少的中间人就可以建立起联系。
- 并非一定要经过6步，只是需要很少的步骤。
- 地铁图
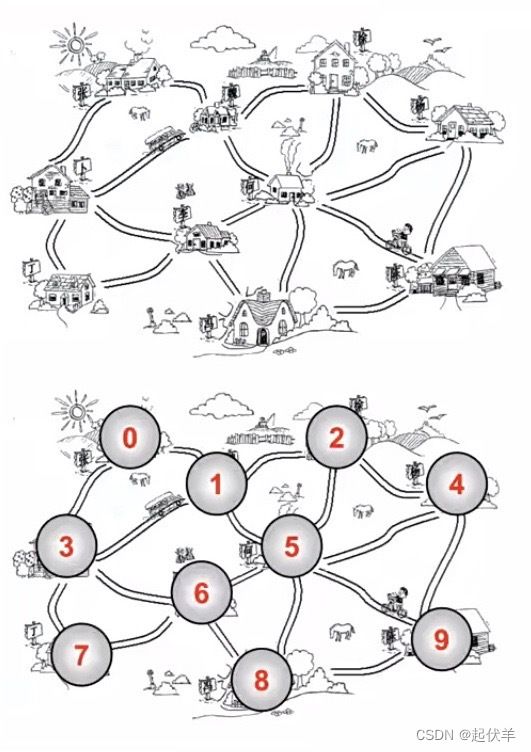
- 村庄之间的关系网
再次 什么是图？
- ❤️ 那么，什么是图呢?
- 我们会发现，上面的节点(其实图中叫顶点Vertex)之间的关系，是不能使用树来表示
- 使用任何的树结构都不可以模拟。
- 这个时候，我们就可以使用图来模拟它们。
- ❤️ 图通常有什么特点呢?
- 一组顶点：通常用 V (Vertex) 表示顶点的集合
- 一组边：通常用 E (Edge) 表示边的集合
- ✓ 边是顶点和顶点之间的连线
- ✓ 边可以是有向的，也可以是无向的。
- ✓ 比如A — B，通常表示无向。 A --> B，通常表示有向
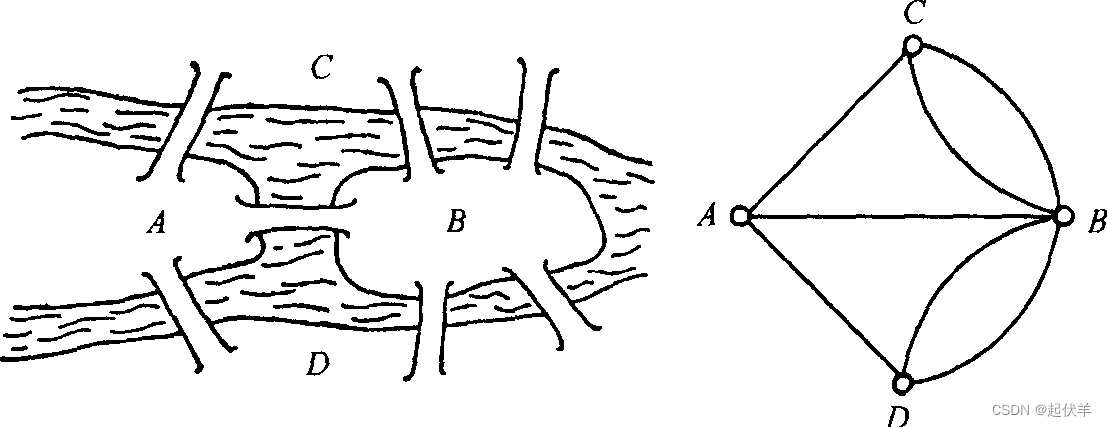
欧拉和七拉问题解法
历史故事
- 8世纪著名古典数学问题之一。
-
在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。
-
有人提出问题： 一个人怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。
-
- 1735年，有几名大学生写信给当时正在俄罗斯的彼得斯堡科学院任职的瑞典天才数学家欧拉，请他帮忙解决这一问题。
- 欧拉在亲自观察了哥伦斯堡的七桥后，认真思考走法，但是始终没有成功，于是他怀疑七桥问题是不是无解的。
- 1736年29岁的欧拉向 彼得斯堡 科学院递交了《哥尼斯堡的七座桥》的论文，在解答问题的同时，开创了数学的一个新的分支——图论与几何拓扑，也由此展开了数学史上的新历程。
欧拉解答
- 他不仅解决了该问题，并且给出了 连通图 可以一笔画的充要条件是：
- 奇点的数目不是0个就是2 个
- 连到一点的边的数目如果是奇数条，就称为奇点
- 如果是偶数条就称为偶点
- 要想一笔画成，必须中间点均是偶点
- 也就是有来路必有另一条去路，奇点只可能在两端，因此任何图能一笔画成，奇点要么没有,要么在两端
- 个人思考：
- 欧拉在思考这个问题的时候，并不是针对某一个特性的问题去考虑，而是将岛和桥抽象成了点和线。
- 抽象是数学的本质，而编程我们也一再强调抽象的重要性。
- 汇编语言是对机器语言的抽象，高级语言是对汇编语言的抽象。
- 操作系统是对硬件的抽象，应用程序在操作系统的基础上构建。
图结构的常见术语
关于术语的概述
-
我们在学习树的时候，树有很多的相关术语。
-
了解这些术语有助于我们更好的理解树结构。
-
我们也来学习一下图相关的术语。
- 但是图的术语其实非常多，如果你找一本专门讲图的各个方面的书籍，会发现 只是术语 就可以 占据满满的一个章节。
- 这里，我们先介绍几个比较常见的术语。
-
我们先来看一个抽象出来的图
用数字更容易我们从整体来观察整个图结构。
术语
-
顶点：
- 顶点刚才我们已经介绍过了，表示图中的一个节点。
- 比如地铁站中某个站/多个村庄中的某个村庄/互联网中的某台主机/人际关系中的人。
-
边：
- 边刚才我们也介绍过了，表示顶点和顶点之间的连线。
- 比如地铁站中两个站点之间的直接连线，就是一个边。
- ❗️ 注意： 这里的边不要叫做路径，路径有其他的概念，待会儿我们会介绍到。
- 之前的图中： 0 - 1有一条边，1 - 2有一条边，0 - 2没有边。
-
相邻顶点：
- 由一条边连接在一起的顶点称为相邻顶点。
- 比如0 - 1是相邻的，0 - 3是相邻的。 0 - 2是不相邻的。
-
度：
- 一个顶点的度是相邻顶点的数量。
- 比如0顶点和其他两个顶点相连，0顶点的度是2
- 比如1顶点和其他四个顶点相连，1顶点的度是4
-
路径：
- 路径是顶点v1，v2…，vn的一个连续序列，比如上图中0 1 5 9就是一条路径。
- 简单路径： 简单路径要求不包含重复的顶点。 比如 0 1 5 9 是一条简单路径。
- 回路： 第一个顶点和最后一个顶点相同的路径称为回路。 比如 0 1 5 6 3 0
-
无向图：
- 上面的图就是一张无向图，因为所有的边都没有方向。
- 比如 0 - 1之间有变，那么说明这条边可以保证 0 -> 1，也可以保证 1 -> 0。
-
有向图：
- 有向图表示的图中的边是有方向的。
- 比如 0 -> 1，不能保证一定可以 1 -> 0，要根据方
向来定。
-
无权图：
- 我们上面的图就是一张无权图(边没有携带权重)
- 我们上面的图中的边是没有任何意义的
- 不能说 0 - 1的边，比4 - 9的边更远或者用的时间更长。
-
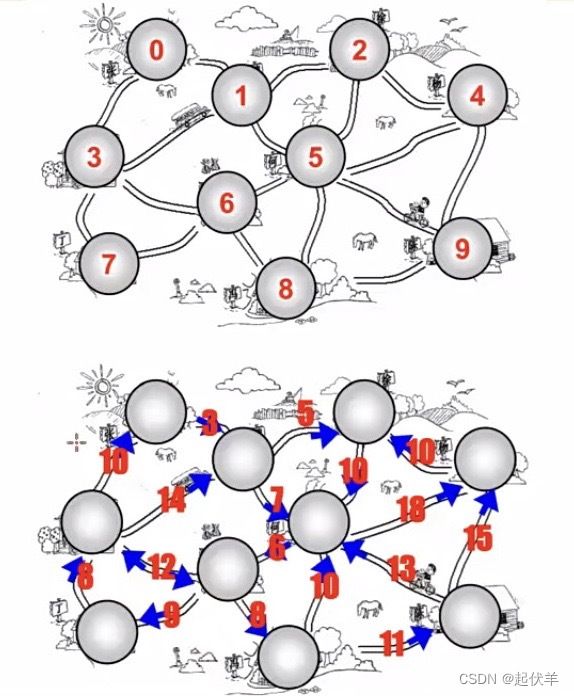
带权图：
- 带权图表示边有一定的权重。
- 这里的权重可以是任意你希望表示的数据：
✓ 比如距离或者花费的时间或者票价。
图的表示
- 怎么在程序中表示图呢?
- 我们知道一个图包含很多顶点，另外包含顶点和顶点之间的连线(边)
- 这两个都是非常重要的图信息，因此都需要在程序中体现出来。
- 顶点的表示相对简单，我们先讨论顶点的表示。
- 上面的顶点，我们抽象成了1 2 3 4，也可以抽象成A B C D。
- 在后面的案例中，我们使用A B C D。
- 那么这些A B C D我们可以使用一个数组来存储起来(存储所有的顶点)
- 当然，A，B，C，D也可以表示其他含义的数据(比如村庄的名字).
- 那么边怎么表示呢?
- 因为边是两个顶点之间的关系，所以表示起来会稍微麻烦一些。
- 下面，我们具体讨论一下变常见的表示方式。
邻接矩阵和邻接表
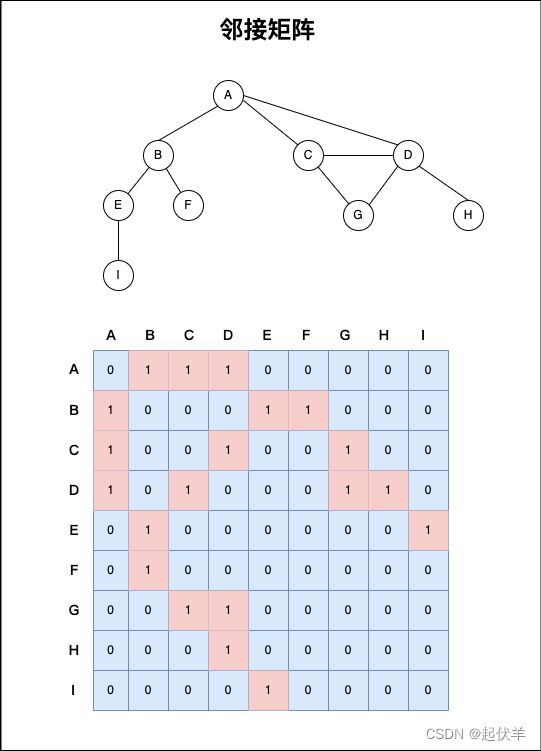
邻接矩阵
- 一种比较常见的表示图的方式： 邻接矩阵。
- 邻接矩阵让每个节点和一个整数项关联，该整数作为数组的下标值。
- 我们用一个二维数组来表示顶点之间的连接。
- 二维数组
[0][2] -> A -> C
- 画图演示：
- 图片解析：
- 在二维数组中，0表示没有连线，1表示有连线。
- 通过二维数组，我们可以很快的找到一个顶点和哪些顶点有连线。(比如A顶点，只需要遍历第一行即可)
- 另外，A - A，B - B(也就是顶点到自己的连线)，通常使用0表示。
- 邻接矩阵的问题：
- 邻接矩阵还有一个比较严重的问题，就是如果图是一个稀疏图
- 那么矩阵中将存在大量的0，这意味着我们浪费了计算机存储空间来表示根本不存在的边。
邻接表
-
另外一种常用的表示图的方式： 邻接表。
- 邻接表由图中每个顶点以及和顶点相邻的顶点列表组成。
- 这个列表有很多种方式来存储： **数组/链表/字典(哈希表)**都可以。
-
画图演示
-
图片解析：
- 其实图片比较容易理解。
- 比如我们要表示和A顶点有关联的顶点(边)，A和B/C/D有边，
- 那么我们可以通过A找到对应的数组/链表/字典，再取出其中的内容就可以啦。
-
邻接表的问题：
- 邻接表计算"出度"是比较简单的(出度： 指向别人的数量，入度： 指向自己的数量)
- 邻接表如果需要计算有向图的"入度"，那么是一件非常麻烦的事情。
- 它必须构造一个**“逆邻接表”，才能有效的计算“入度”。但是开发中“入度”**相对用的比较少。
创建图类
- 先创建Graph类
- 代码解析
- 创建Graph的构造函数，这个我们在封装其他数据结构的时候已经非常熟悉了。
- 定义了两个属性：
✓ vertexes： 用于存储所有的顶点，我们说过使用一个数组来保存。
✓ adjList： adj是adjoin的缩写，邻接的意思。 adjList用于存储所有的边，我们这里采用邻接表的形式。 - 之后，我们来定义一些方法以及实现一些算法就是一个完整的图类了。
class Graph<T> {
// 顶点
vertexes: T[] = [];
// 邻接表
adjList: Map<T, T[]> = new Map();
}
添加方法
- 现在我们来增加一些添加方法。
- 添加顶点： 可以向图中添加一些顶点。
- 添加边： 可以指定顶点和顶点之间的边。
- 添加顶点
- 代码解析：
- 我们将添加的顶点放入到数组中。
- 另外，我们给该顶点创建一个数组[]，该数组用于存储顶点连接的所有的边.(回顾邻接表的实现方式)
- 代码解析：
- 添加边
- 代码解析：
- 添加边需要传入两个顶点，因为边是两个顶点之间的边，边不可能单独存在。
- 根据顶点v取出对应的数组，将w加入到它的数组中。
- 根据顶点w取出对应的数组，将v加入到它的数组中。
- 因为我们这里实现的是无向图，所以边是可以双向的。
- 代码解析：
// 添加顶点
addVertex(vertex: T) {
// 将顶点添加到顶点数组中保存
this.vertexes.push(vertex);
// 创建一个邻接表的数组
this.adjList.set(vertex, []);
}
addEdge(v1: T, v2: T) {
this.adjList.get(v1)?.push(v2);
this.adjList.get(v2)?.push(v1);
}
printEdges方法
-
为了能够正确的显示图的结果，我们来实现一下Graph的printEdges方法
-
测试代码:
const graph = new Graph(); graph.addVertex('A'); graph.addVertex('B'); graph.addVertex('C'); graph.addVertex('D'); graph.addVertex('E'); graph.addVertex('F'); graph.addVertex('G'); graph.addVertex('H'); graph.addVertex('I'); graph.addEdge('A', 'B'); graph.addEdge('A', 'C'); graph.addEdge('A', 'D'); graph.addEdge('C', 'D'); graph.addEdge('C', 'G'); graph.addEdge('D', 'G'); graph.addEdge('D', 'H'); graph.addEdge('B', 'E'); graph.addEdge('B', 'F'); graph.addEdge('E', 'I'); graph.printEdges();- 运行结果：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fK63qbI7-1692005552724)(/Volumes/web/数据结构与算法（ts）/截图/截屏2023-08-14 15.37.06.png “运行结果”)]
- 运行结果：
图的遍历
图的遍历思想
图的遍历思想和树的遍历思想是一样的。
图的遍历意味着需要将图中每个顶点访问一遍，并且不能有重复的访问
- 有两种算法可以对图进行遍历
- 广度优先搜索(Breadth-First Search，简称BFS)
- 深度优先搜索(Depth-First Search，简称DFS)
- 两种遍历算法，都需要明确指定第一个被访问的顶点。
- 它们的遍历过程分别是怎么样呢?
- 我们以一个迷宫中关灯为例。
- 现在需要你进入迷宫，将迷宫中的灯一个个关掉，你会怎么关呢?
遍历的思想
- 两种算法的思想：
- BFS： 基于队列，入队列的顶点先被探索。
- DFS： 基于栈或使用递归，通过将顶点存入栈中，顶点是沿着路径被探索的，存在新的相邻顶点就去访问。
- 为了记录顶点是否被访问过，我们使用三种颜色来反应它们的状态
- 白色： 表示该顶点还没有被访问。
- 灰色： 表示该顶点被访问过，但并未被探索过。
- 黑色： 表示该顶点被访问过且被完全探索过。
- 或者我们也可以使用Set来存储被访问过的节点。
广度优先搜索
-
广度优先搜索算法的思路 ：
- 广度优先算法会从指定的第一个顶点开始遍历图，先访问其所有的相邻点，就像一次访问图的一层。
- 换句话说，就是先宽后深的访问顶点
-
图解BFS
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mNFb1uIZ-1692005552726)(/Volumes/web/数据结构与算法（ts）/画图/图/广度优先搜索.png “广度优先搜索”)]
◼ 广度优先搜索的实现：
◼ 创建一个队列Q。 -
代码 ：
// 广度优先
bfs() {
// 1. 判断是否有顶点
if (this.vertexes.length === 0) return;
// 2. 创建队列结构来访问每个顶点
const queue: T[] = [];
queue.push(this.vertexes[0]);
// 3. 创建Set，来记录一个顶点是否被访问过
const visited = new Set();
visited.add(this.vertexes[0]);
// 4. 遍历队列中每一个顶点
while (queue.length) {
// 4.1 访问队列中第一个顶点
const vertex = queue.shift()!;
console.log(vertex);
// 4.2 取出相邻的顶点
const neighbors = this.adjList.get(vertex);
if (!neighbors) continue;
for (const neighbor of neighbors) {
if (!visited.has(neighbor)) {
visited.add(neighbor);
queue.push(neighbor);
}
}
}
}
- 运行结果：
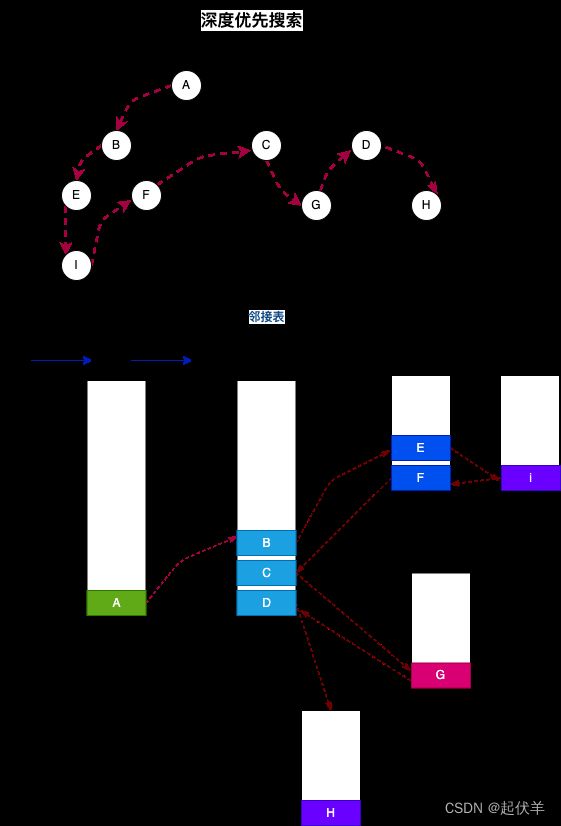
深度优先搜索
-
深度优先搜索的思路：
- 深度优先搜索算法将会从第一个指定的顶点开始遍历图，沿着路径知道这条路径最后被访问了。
- 接着原路回退并探索下一条路径。
-
深度优先搜索
- 深度优先搜索算法的实现：
- 广度优先搜索算法我们使用的是队列，这里可以使用栈完成，也可以使用递归。
- 深度优先搜索算法的实现：
-
图DFS
-
代码 ：
// 深度优先
dfs() {
// 1. 判断有没有顶点，没有直接返回
if (this.vertexes.length === 0) return;
// 2.创建栈结构
const stack: T[] = [];
stack.push(this.vertexes[0]);
// 3. 创建Set结构
const visited = new Set();
visited.add(this.vertexes[0]);
// 4. 从第一个顶点开始访问
while (stack.length) {
const vertex = stack.pop()!;
console.log(vertex);
// 取出相邻的顶点
const neighbors = this.adjList.get(vertex);
if (!neighbors) continue;
for (let i = neighbors.length - 1; i >= 0; i--) {
const nei = neighbors[i];
if (!visited.has(nei)) {
visited.add(nei);
stack.push(nei);
}
}
}
}
- 运行结果：
图结构的常见建模
- 对交通流量建模
- 顶点可以表示街道的十字路口，边可以表示街道。
- 加权的边可以表示限速或者车道的数量或者街道的距离。
- 建模人员可以用这个系统来判定最佳路线以及最可能堵车的街道。
- 对飞机航线建模
- 航空公司可以用图来为其飞行系统建模。
- 将每个机场看成顶点，将经过两个顶点的每条航线看作一条边。
- 加权的边可以表示从一个机场到另一个机场的航班成本，或两个机场间的距离。
- 建模人员可以利用这个系统有效的判断从一个城市到另一个城市的最小航行成本。