HoudiniVex笔记_P23_SDFBasics有向距离场
原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili
Houdini版本：19.5
1、什么是SDF
Houdini支持两种体积类型，它自己的体积格式（也有两种，Fog 和SDF ）和VDB格式。
Volume的两种类型：Fog volume和SDF volume。是Houdini自带的不同类型的体积，特点是每个体素都有值。Volume(体积)由voxel（体积元素，后面简称为体素）组成。
Fog volume实际是储存了每个体素的密度，常应用于流体模拟等。(想了解可以前面的第10节笔记)
SDF volume中(SDF Signed Distance Filed 是带符号的距离场)，每个体素存储了一个数值，数值大小表示到表面的距离，正数代表在物体外，负数代表在物体内，0表示在物体表面(需要精度较高)。所以将几何体转化为碰撞物的时候，实质就是转化为SDF，利用体素的数值来判断是否发生碰撞等。
更多体积相关可以看这篇文章的简单介绍：Houdini中体积SDF/fog/volume/db的一些理解和区别
2、SDF节点及参数
①创建一个类型为Polygon的Sphere节点，再添加一个vdbfrompolygons节点，及一个VolumeWrangle节点，
②用上面为例，讲讲vdbfrompolygons节点的一些设置，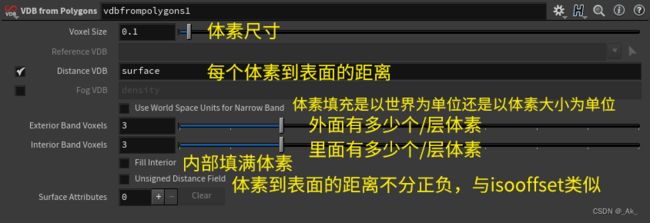
③我们仅保留点，看看vdbfrompolygons节点设置的具体表现，
第三、四、五张图为用点代替体素，的一个截面，
3、volumegradient函数
volumegradient() 函数返回一个向量值，该值为距离值递增方向的矢量值（下面试试让这个值代替体素的法线），（gradient的中文感觉总差点意思，后面还是以英文代替吧），
4、使用Fog Volume可视化SDF值
挺简单的，还是记录下，
5、使用VEX对SDF轮廓简单修改
可以直接修改SDF的【@surface】值，来实现物体表面/轮廓的改变（对轮廓进行偏移操作），
值相加，物体的表面/轮廓向内偏移，即收缩；
值相减，物体的表面/轮廓向外偏移，即扩大；
eg.简单记录下，感兴趣可以试试，
6、Exercise—修改SDF轮廓与Animated
基于时间和三角函数，对SDF轮廓进行动态修改。
eg.直接使用【5、使用VEX对SDF轮廓简单修改】的案例，仅对VolumeWrangle节点进行修改，
float val = sin(@P.y * $PI * chi('num') + @Time * 10) * chf('dist');
f@surface += val;结果为：在 num = 6，dist = 0.07条件下，
7、修改SDF的Gradient值
还是基于三角函数对物体轮廓进行偏移，比上面的稍微复杂一丢丢， 不晓得可以应用到哪方面（云层？），还是记录下。
eg.先上结果，
①节点及设置如下，
②对offset_with_voxel_val_and_gradient节点的一些补充，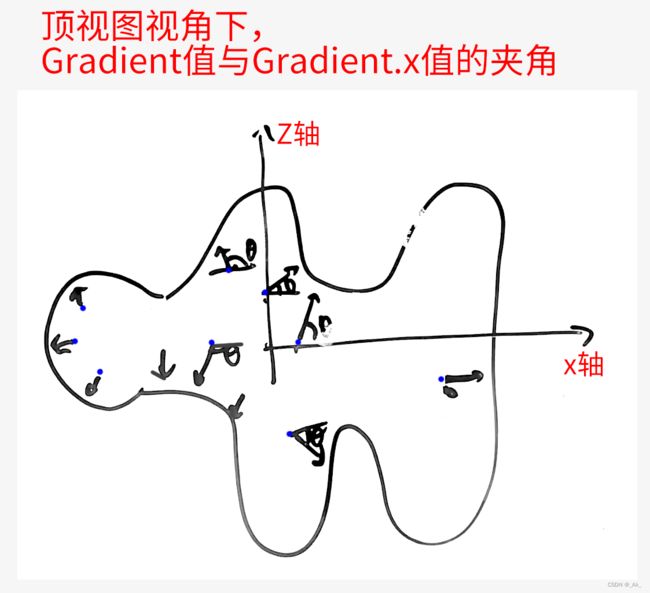
float val = f@surface;
vector dir = volumegradient(0, 'surface', @P);
//顶视图视角下，Gradient值与dirXZ.x值的夹角
vector dirXZ = dir;
dirXZ.y = 0.0;
dirXZ = normalize(dirXZ);
float ang = atan2(dirXZ.z, abs(dirXZ.x));
//atan2返回两个向量之间的夹角
//因为atan2三角函数范围是-π到π，所以使用绝对值abs，使其范围为0到π
//多重映射
float v = sin(ang * chi('num')); //值范围-1到1
v = fit11(v, 0, 1.0); //重映射，值范围0到1
v = chramp('ramp', v); //继续重映射，随便设
v = fit01(v, 0.0, chf('dist')); //重映射，值范围0到【自定义】
f@surface += v; //结合sin函数的规律，去理解v值的变化8、SDF与基础碰撞
挺简单的，仅记录下，
9、Exercise—SDF碰撞与Animated
与上类似，不过这次加入解算器，让小球在Grid上转动，也不算复杂，记录下，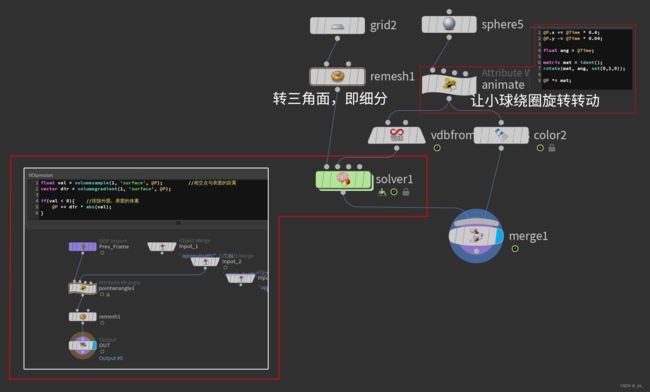
10、Exercise—SDF Gradient与向量Animation
点由内向外运动，运动方向位gradient。
eg.先上结果，原模型为橡皮模型，
①节点连接及设置，（代码在下一个案例），
11、基于SDF的扩展向量场
大概与上类似，不过加入了curlnoise() 噪波函数，让其运动起来跟随噪波特性(随机但又有序)。
eg.先上结果，
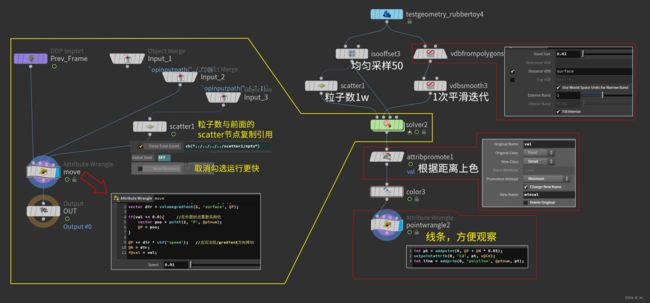
①直接使用【10、Exercise—SDF Gradient与向量Animation】的案例，下图为节点连接及设置，相同设置部分不再赘述，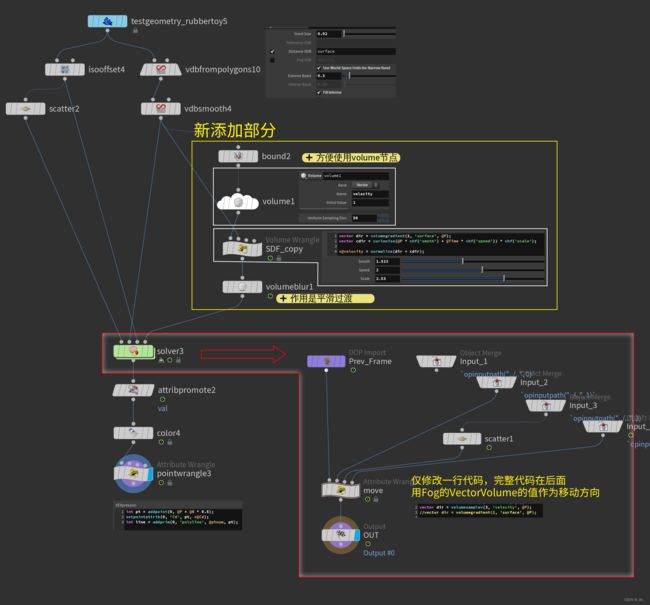
② 完整代码如下，
// copy SDF节点代码
vector dir = volumegradient(1, 'surface', @P);
vector cdir = curlnoise(@P * chf('smoth') + @Time * chf('speed')) * chf('scale');
v@velocity = normalize(dir + cdir);// move节点代码
float val = volumesample(1, 'surface', @P);
vector dir = volumesamplev(3, 'velocity', @P);
//vector dir = volumegradient(1, 'surface', @P);
if(val >= 0.0){ //在轮廓外面的点重新实例化
vector pos = point(2, 'P', @ptnum);
@P = pos;
}
@P += dir * chf('speed'); //点沿法线/gradient方向移动
@N = dir;
f@val = val;// pointwrangle3节点代码（最后一个节点）
int pt = addpoint(0, @P + @N * 0.5);
setpointattrib(0, 'Cd', pt, v@Cd);
int line = addprim(0, 'polyline', @ptnum, pt);