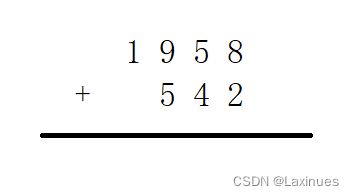【高精度】 C语言实现高精度加法
目录
1. 前言
2. 高精度及其思想方法介绍
3. C语言实现高精度加法
3.1存数字
3.2 计算 存结果
3.3 倒序打印
4.0 结语
1. 前言
本系列主要介绍 高精度加减高精度,高精度乘除低精度。后续会持续更新,敬请期待吧!
本文主要介绍的是高精度加高精度。话不多说,我们进入正题。
2. 高精度及其思想方法介绍
一般来说int类型最大能储存的数字为![]() ~(
~(![]() ),longlong则是
),longlong则是![]() ~(
~(![]() )。
)。
那当我们计算的数字超过了这个范围,我们该如何用代码进行运算呢?这就是我接下来要介绍的高精度运算,所谓高精度运算,简单来讲就是大数值之间的运算。若想使用代码来实现这个运算,需要用到小学时就接触的竖式计算思想。这里为了方便,我会使用一些数值较小的数来进行讲解高精度加法。
相信大家对竖式运算一定得心应手吧,试想我们输入了两个特别大的数,(这两个数该储存在哪里?)两个数按照竖式计算来相加,最后输出结果,这是我们想要得到的。
那具体如何实现呢?
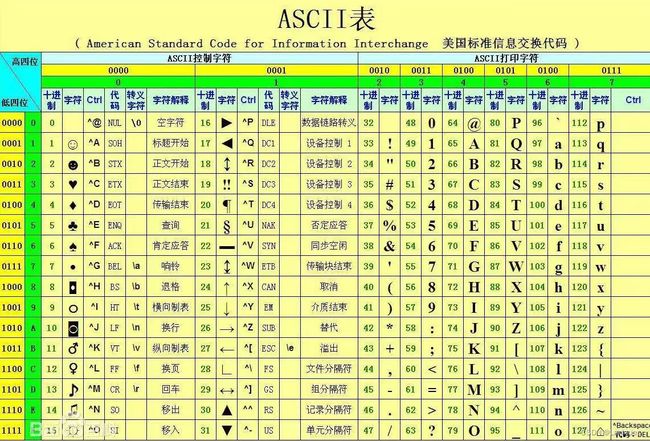
我们知道,数值再大,换个角度,也只是数字排列顺序与数字多少的问题,这里我们运用char 类型的数组,便可以实现储存大数值的目标。而且字符的本质也是整数!如下表
有了ascll表,我们便有思路将字符变为数字。整体思路可以分成
存数字 — 计算 — 存结果 — 打印结果 这4步。
3. C语言实现高精度加法
3.1存数字
我们用char数组来接收两个数字。
但是在计算前,我们应该思考一个这样的问题,十进制计算有一个进一的计算 。如果1958的1对应数组的下标0,那是否会使得我们无法进一呢?因此,我们需要将数字倒序存入另一组数组中进行计算!
//倒序初始数组
int inverse_order(char str[], int len,int k)
{
return (str[len- k] - '0');
}
int main()
{
printf("请输入两个数\n");
//用str数组来接收两个数
char str1[10] = { 0 };
scanf("%s", str1);
char str2[10] = { 0 };
scanf("%s", str2);
//准备两个数组准备倒序
int arr1[10] = { 0 };
int arr2[10] = { 0 };
//倒叙
int i = 0;
arr1[0] = strlen(str1);
for (i = 1; i <= arr1[0]; i++)
{
//倒序函数
arr1[i] = inverse_order(str1, strlen(str1), i);
}
arr2[0] = strlen(str2);
for (i = 1; i <= arr2[0]; i++)
{
//倒序函数
arr2[i] = inverse_order(str2, strlen(str2),i);
}
}char数组中的字符‘9’ - ‘0’后,ascll码值会变为9,此时变为真正的数字9!
这样,我们便得到了两个倒序存储着数字的数组arr1和arr2。
3.2 计算 存结果
计算是本文的重点,处理竖式计算,需要将下标相同的元素相加,通过处理实现留下个位数,以及进一。并且,我们需要将运算后的数值储存起来。
//比大小函数
int MAX(int x, int y)
{
return x > y ? x : y;
}
//加法函数
void sum(int ARR1[],int ARR2[],int ARR3[])
{
//我们用ARR3[0]来记录ARR3[]的数组长度!!!!!
//我们用ARR3[0]来记录ARR3[]的数组长度!!!!!
//我们用ARR3[0]来记录ARR3[]的数组长度!!!!!
int i = 0;
ARR3[0] = MAX(ARR1[0], ARR2[0]);
int tmp = 0;
for (i = 1; i <= ARR3[0] + 1; i++)
{
//取个位数,并且进一
ARR3[i] = (ARR1[i] + ARR2[i] + tmp) % 10;
//判断是否进一
tmp = (ARR1[i] + ARR2[i] + tmp) / 10;
}
if (tmp != 0)
{
//最大计数单位进一
ARR3[++ARR3[0]]++;
}
int main()
{
//准备一个数组用来存入两数相加后的数据
int sum1[10] = { 0 };
//将两数和的数据存入sum1中
sum(arr1, arr2, sum1);
}这种算法不同于普通加减乘除,可以完成一些高精度的运算。就是比较麻烦。
3.3 倒序打印
倒序打印主要是找到数位最大的那个数字,运用普通方法进行打印即可,详情看代码和注释!!
//倒序打印函数
void print(int final_arr[])
{
//left也可以撤掉,但是为了好理解还是留下了
int left = 1;
int right = 0;
int i = 0;
for (i = 9; i > 0; i--)
{
//用来寻找第一个不为0的数进行打印,因为最高计数单位的数字不可能是0.
if (final_arr[i] != 0)
{
right = i;
break;
}
}
//从右往左打印,恢复正常顺序
printf("两数和为:\n");
while (left <= right)
{
printf("%d", final_arr[right]);
right--;
}
}4.0 结语
把完整的码写给大家
//高精度加高精度
#include
//倒序初始数组
int inverse_order(char str[], int len,int k)
{
return (str[len- k] - '0');
}
//比大小函数
int MAX(int x, int y)
{
return x > y ? x : y;
}
//加法函数
void sum(int ARR1[],int ARR2[],int ARR3[])
{
int i = 0;
ARR3[0] = MAX(ARR1[0], ARR2[0]);
int tmp = 0;
for (i = 1; i <= ARR3[0] + 1; i++)
{
ARR3[i] = (ARR1[i] + ARR2[i] + tmp) % 10;
tmp = (ARR1[i] + ARR2[i] + tmp) / 10;
}
if (tmp != 0)
{
ARR3[++ARR3[0]]++;
}
}
//倒序打印函数
void print(int final_arr[])
{
int left = 1;
int right = 0;
int i = 0;
for (i = 9; i > 0; i--)
{
if (final_arr[i] != 0)
{
right = i;
break;
}
}
printf("两数和为:\n");
while (left <= right)
{
printf("%d", final_arr[right]);
right--;
}
}
int main()
{
printf("请输入两个数\n");
//用str数组来接收两个数
char str1[10] = { 0 };
scanf("%s", str1);
char str2[10] = { 0 };
scanf("%s", str2);
//准备两个数组准备倒序
int arr1[10] = { 0 };
int arr2[10] = { 0 };
//倒叙
int i = 0;
arr1[0] = strlen(str1);
for (i = 1; i <= arr1[0]; i++)
{
arr1[i] = inverse_order(str1, strlen(str1), i);
}
arr2[0] = strlen(str2);
for (i = 1; i <= arr2[0]; i++)
{
arr2[i] = inverse_order(str2, strlen(str2),i);
}
//准备一个数组用来存入两数相加后的数据
int sum1[10] = { 0 };
//将两数和的数据存入sum1中
sum(arr1, arr2, sum1);
//倒序打印存有两数和的数组
print(sum1);
return 0;
} 到这里,高精度加法的具体实现方法已经讲解完毕。接下来会更新高精度减高精度,高精度乘除低精度。关注作者不迷路哦,请多多支持我(三连!!!),一起进步吧!