Codeforces Round 893 (Div. 2)ABC
Codeforces Round 893 (Div. 2)
目录
- A. Buttons
-
- 题目大意
- 思路
- 核心代码
- B. The Walkway
-
- 题目大意
- 思路
- 核心代码
- C. Yet Another Permutation Problem
-
- 题目大意
- 思路
- 核心代码
A. Buttons
题目大意
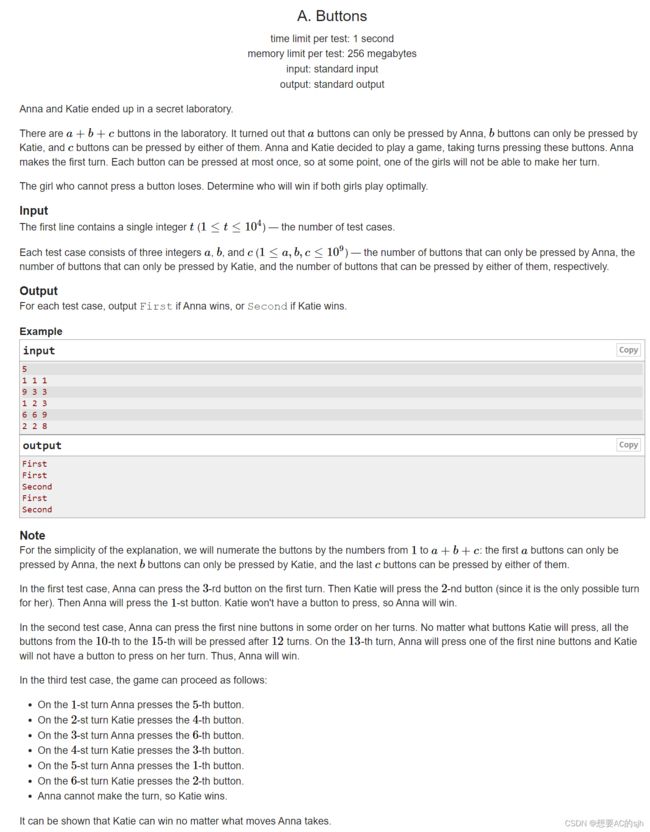
一共有三个盒子分别是a、b、c,第一个人只能拿a、c,第二个人只能拿b、c,两个人轮流拿,谁先无法操作谁输,每次只能拿一个
翻译:
安娜和凯蒂最后进了一个秘密实验室。
实验室里有a+b+c按钮。结果是a按钮只能由Anna按下,b按钮只能由Katie按下,c按钮可以由她们中的任何一个按下。安娜和凯蒂决定玩一个游戏,轮流按这些按钮。安娜拐了第一个弯。每个按钮最多只能按一次,所以在某些时候,其中一个女孩将无法轮到她。
不会按按钮的女孩就输了。如果两个女孩都打得最好,决定谁赢。
输入 第一行包含一个整数t(1≤t≤104)——测试用例的数量。
每个测试用例由三个整数a,b,c组成(1≤a,b,c≤109),分别是Anna只能按下的按钮数,Katie只能按下的按钮数,以及她们任意一个都能按下的按钮数。
输出 对于每个测试用例,如果Anna赢了,输出First,如果Katie赢了,输出Second。
思路
两个人肯定优先拿c盒子里面的物品,所以直接判断c盒子的奇偶性然后再判断a、b盒子之间的关系即可
核心代码
void solve()
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(c%2==0)
{
if(a<=b)printf("Second\n");
else printf("First\n");
}
else
{
if(a<=b-1)printf("Second\n");
else printf("First\n");
}
}
B. The Walkway
题目大意
这道题目太烦人了,首先Petya(一下简称P)会经过n个长凳,有些长凳会有买饼干的人,满足下面的条件之一P就会吃饼干:
- 当前的长凳编号是1,也就是一开始的时候
- 此时长凳有一个卖饼干的,P买一个饼干吃
- P已经间隔了k个长凳没有吃饼干了,此时吃自己的饼干
注意这里同时满足的话可以选择吃自己的饼干,每一个长凳只会吃一个饼干
问:如果去掉一个卖饼干的,最少只需要吃多少个饼干,此时还需要卖多少个饼干
具体的还是看翻译叭
翻译:
暑期信息学学校的主走道附近有n个长椅。这些长凳用从1到n的整数编号
为了让他们跟随。走道附近也有卖饼干的。第i(1≤i≤m)个饼干销售商位于第si个工作台附近。彼佳站在走道的开头。从第1号板凳开始到第n号板凳结束,他将超过所有板凳。Petya在1分钟内通过了两个连续长凳之间的距离。他的背包里有无数的饼干。Petya打算吃他背包里的饼干,然后在走路的时候从卖饼干的人那里买。
Petya只在长凳附近吃饼干,根据以下规则:当且仅当至少满足以下条件之一时,Petya将在第i(1≤i≤n)个长凳附近吃饼干:
1、 在第i条长凳附近有一个卖饼干的人。然后Petya会从卖饼干的那里买一块饼干,然后马上吃掉。
2、Petya还没有吃过饼干。然后,彼佳会从背包里拿出一块饼干,马上吃掉。
3、距离彼佳吃上一块饼干至少已经过去了d分钟。换句话说,Petya没有在长椅i−1,i−2,…,max(i−d+1,1)附近吃饼干。然后,彼佳会从背包里拿出一块饼干,马上吃掉。你可能会认为Petya会立刻吃掉饼干。Petya不会在同一条长凳附近吃两块或更多的饼干。你要尽量减少Petya走路时吃的饼干的数量。为了做到这一点,你将要求暑期信息学校的管理人员在Petya开始行走之前从人行道上移除一个饼干小贩。
请确定在移除一个饼干卖家后Petya可以吃的最小饼干数量。还要确定卖饼干的人的数量,这样如果你去掉其中一个,Petya就会吃掉尽可能少的饼干。
输入 第一行包含一个整数t(1≤t≤103)——测试用例的数量。
每个测试用例的第一行包含三个整数n,
m和d(2≤d≤n≤109,2≤m≤min(105,n)),分别是长凳的数量,饼干销售商的数量和语句中参数d的值。每个测试用例的第二行包含m个整数s1,s2,…,sm(1≤si≤n) ) -售卖饼干的小贩的位置。对于所有1≤i≤m−1,保证si1。
可以保证m在所有测试用例上的总和不超过105。
输出
对于每个测试用例,打印两个整数—如果只删除一个cookie销售者,Petya可以吃的最小cookie数量,以及如果删除其中一个cookie销售者,Petya将吃掉的最小可能数量的cookie数量。
思路
我们可以把每一个饼干商人作为一个计算的节点,因为后面我们需要计算删除一个饼干商人的时候的最优情况,我们可以发现不管我们怎么样删除,只会影响相邻两个商人之间吃的饼干数量以及购买饼干的数量,所以每一个商人作为一个计算的节点,特别的我们分开来计算,分别使用数组b表示每一次遇到商人的时候我们在第i个商人这里需要购买的饼干数量,再使用数组c表示从第i-1个商人到第i个商人之间我们需要自己吃掉多少个饼干,遍历一遍计算好所有的节点然后对每一个商人进行分析,前面讲到商人只会影响相邻的两个商人之间的饼干数量,所以就再遍历一遍,每一次计算减少的数量同时计算达到最小值的次数,最后直接输出结果
核心代码
void solve()
{
int n,m,d;
scanf("%d%d%d",&n,&m,&d);
int a[N]{0},b[N]{0},c[N]{0};
for(int i=1;i<=m;++i)
scanf("%d",&a[i]);
ll sum_b=0,sum_c=0;
a[0]=1;
sum_c++;
a[m+1]=n;
int ans=0;
for(int i=1;i<=m+1;++i)
{
c[i]=(a[i]-a[i-1])/d;
sum_c+=c[i];
if((a[i]-a[i-1])%d==0||i==m+1)continue;
b[i]=1;
sum_b++;
}
int minzhi=INT_MAX,minweizhi=0;
int shangjia=INT_MAX;
for(int i=1;i<=m;++i)
{
int ziji=(a[i+1]-a[i-1])/d;
int shang;
if((a[i+1]-a[i-1])%d==0)shang=0;
else shang=1;
if(i==m)shang=0;
if((ziji+shang)-(c[i]+c[i+1]+b[i]+b[i+1])<minzhi)
{
minzhi=(ziji+shang)-(c[i]+c[i+1]+b[i]+b[i+1]);
minweizhi=i;
int sum0=0;
for(int k=0;k<=m+1;++k)
{
if((k!=i)&&(k!=i+1))sum0+=b[k];
}
ans=1;
sum0+=shang;
shangjia=sum0;
}
else if((ziji+shang)-(c[i]+c[i+1]+b[i]+b[i+1])==minzhi)ans++;
int zhi=b[i]+b[i+1];
}
printf("%lld %d\n",(ll)(sum_b+sum_c+(ll)minzhi),ans);
}
C. Yet Another Permutation Problem
题目大意
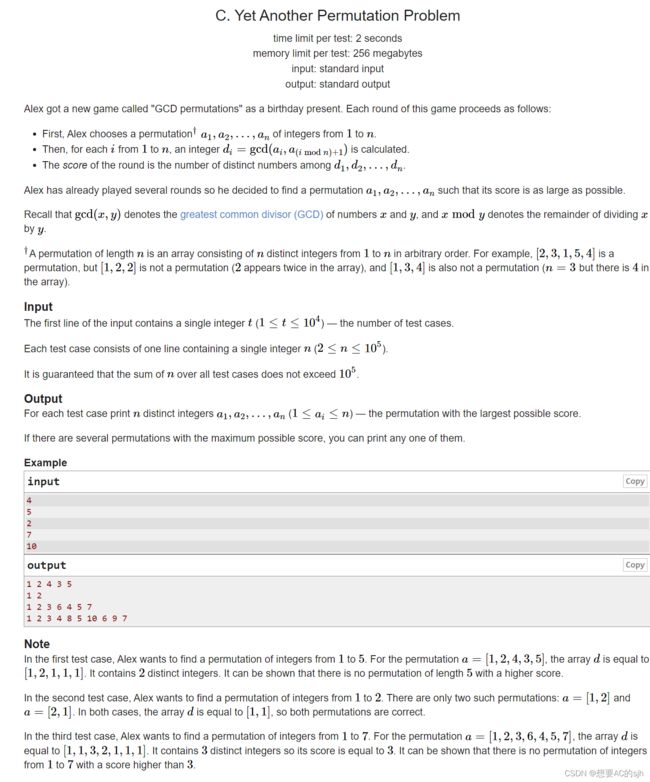
给定一个数字n,找出n的全排列组合中能够使得d1、d2、…、dn中不同的数字尽可能多,对于每一个di:
di=gcd(ai,a(imodn)+1)
翻译:
亚历克斯得到了一个名为“GCD排列”的新游戏作为生日礼物。本游戏每轮进行如下:
首先,Alex选择一个从1到n的整数组合†a1,a2,…,an。
然后,对于从1到n的每个i,计算一个整数di=gcd(ai,a(imodn)+1)。这一轮的得分是d1,d2,…,dn中不同数字的个数。Alex已经玩了好几轮了,所以他决定找到一个a1,a2,…的排列,这样它的得分就尽可能的大。回想一下,gcd(x,y)表示数x和y的最大公约数(gcd), x mod y表示x除以y的余数。
长度为n的排列是由n个不同的整数以任意顺序从1到n组成的数组。例如,[2,3,1,5,4]是一个排列,但[1,2,2]不是一个排列(2在数组中出现两次),并且[1,3,4]也不是一个排列(n=3,但数组中有4)。
输入 输入的第一行包含一个整数t(1≤t≤104)——测试用例的数量。
每个测试用例由一行组成,其中包含单个整数n(2≤n≤10^5)。
可以保证所有测试用例的n之和不超过105。
输出 对于每个测试用例,打印n个不同的整数a1,a2,…,an(1≤ai≤n) -具有最大可能得分的排列。
如果有几个排列具有最大可能的分数,您可以打印其中的任何一个。
思路
要想要不同的数字尽可能的多,就要尽量用上每一个数字,可以发现:
gcd(n,2n)=n,所以我们尽量安排每一个数都是前面的数字的两倍,剩下的数字就往后面排用同样的方法排
核心代码
void solve()
{
int n;
scanf("%d",&n);
bool a[N]{0};
int cnt=1;
for(int i=1;i<=n;++i)
{
if(!a[i])
{
cnt=i;
while(cnt<=n)
{
a[cnt]=1;
printf("%d ",cnt);
cnt<<=1;
}
}
}
printf("\n");
}